Приближенные построения разверток

Развертку неразвертывающихся поверхностей вращения строят приближенно.

1. СПОСОБ ЦИЛИНДРОВ. Способ состоит в том, что данную поверхность вращения разбивают с помощью меридианов на сравнительно узкие, равные между собой доли. Каждую такую долю заменяют описанной цилиндрической поверхностью, которая касается данной поверхности в точках среднего меридиана доли. Этот средний меридиан будет вместе с тем нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю.

Пример. Построить развертку данной сферы (рис. 169). Разобьем сферу при помощи меридианов на шесть равных частей. Рассмотрим построение приближенной развертки одной части сферы, средним меридианом которой является главный меридиан f.

Рис. 169

Прежде всего заменим эту часть сферы цилиндрической поверхностью, описанной около нее. Образующие этой поверхности будут фронтально проецирующими прямыми и поэтому проецируются в натуральную величину на горизонтальную плоскость проекций H. Нормальным сечением цилиндрической поверхности будет половина главного меридиана f, а границами поверхности будут плоскости меридианов, ограничивающих рассматриваемую часть.

Для построения развертки этой цилиндрической поверхности заменяем ее вписанной призматической поверхностью. Для этого делим половину главного меридиана на шесть равных частей и через точки деления проводим образующие цилиндрической поверхности. Затем спрямляем полумеридиан f в отрезок прямой и через его точки деления проводим перпендикулярно к нему образующие EF = EF = E₁F₁, CD = CD = C₁D₁ и т.д.

Соединив концы этих образующих плавными кривыми, получим приближенную развертку одной доли данной сферы, равной 1/6 ее части. Развертки остальных долей являются повторением первой.

Обычно сферу разбивают на двенадцать и более частей для получения более точной ее развертки.

2. СПОСОБ КОНУСОВ. Этот способ состоим в замене неразвертывающихся поверхностей такой другой поверхностью, которая составлена из нескольких конических и, следовательно, развертываемых элементов.

Построение развертки способом конусов показано на примере поверхности вращения произвольного вида (рис. 170).

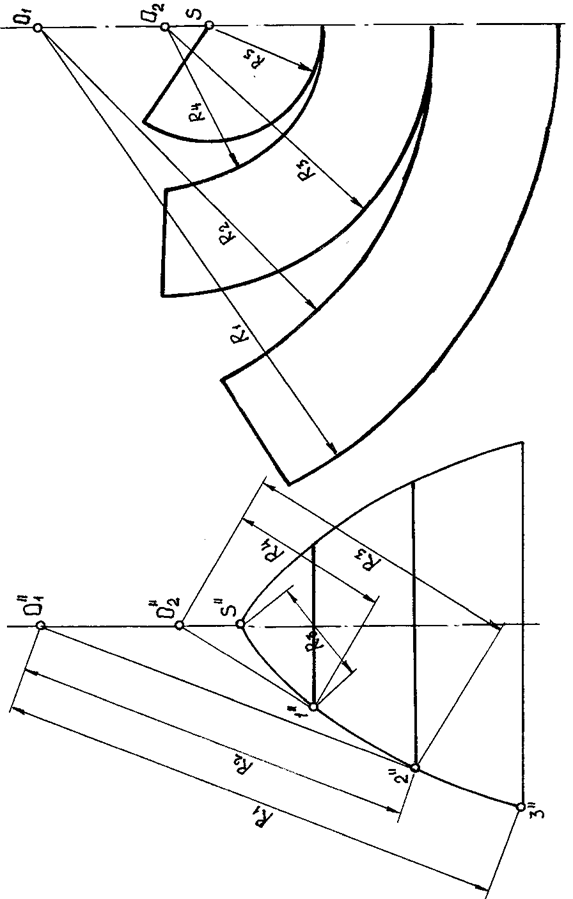
Рис. 170

Разделим данную поверхность на несколько поясов, проходящих через точки 1(1”), 2(2”), 3(3”) главного меридиана (рис. ).

Каждый из трех выделенных поясов заменим конусом: первый и второй — описанным около данной поверхности, а третий — вписанным в эту поверхность (рис. 170).

Построение приближенной развертки заданной поверхности сводится к построению разверток трех конусов.

Границами между отдельными частями развертки являются параллели развертываемой поверхности вращения, переходящие в дуги окружностей, которые должны совпадать. Так, длины дуг, имеющих радиусы R₂ и R₃ и радиусы R₄ и R₅, попарно равны и могут легко определяться построением, как показано на рис. 109.

БИБЛИОГРАФИЧЕСКИ СПИСОК

1. Белов Н.М. Курс начертательной геометрии. - Л., Стройиздат, 1971. - 189 с.

2. Будасов Б.В., Каминский В.П. Строительное черчение. - М.: Стройиздат, 1990. - 464 с.

3. Виницкий И.Н. Начертательная геометрия. - М., Высшая школа,1975. - 280 с.

4. Климухин А.Г. Тени и перспектива. - М.: Стройиздат, 1967.- 199 с.

5. Короев Ю.И. Начертательная геометрия. - М.: Стройиздат, 1987.- 319с.

6. Короев Ю.И. Строительное черчение и рисование. - М.: Высшая школа, 1983. - 288 с.

7. Короев Ю.И. Черчение для строителей. - М.: Высшая школа, 1985.- 128 с.

8. Крылов Н.Н. Начертательная геометрия. - М., Высшая школа, 1990. - 245 с.

9. Кузнецов Н.С. Начертательная геометрия. - М.: Высшая школа, 1981. - 262 с.

10. Русскевич Н.Л. Начертательная геометрия.-К.: Вища шк., 1978.-312 с.

11. Русскевич Н.П., Ткач Д.И., Ткач М.Н. Справочник по инженерно-строительному черчению. - К.: Будiвельник, 1987. - 264 с.

12. Фролов С.А. Начертательная геометрия. - М.: Машиностроение, 1983, - 240 с.

Рассмотрено на заседании СОГЛАСОВАНО

кафедры 26 июня 1998 г. Ответственный

Зав. кафедрой НГиИГ за стандартизацию на кафедре

____________ Карцева Г.М.

___________ Васин С.А. " 26 " июня 1998 г.

* "-— êâàíòîð îáùíîñòè, ÷èòàåòñÿ: äëÿ âñÿêîãî (äëÿ ëþáîãî)

* Новая ось x₁ и плоскость проекции V₁ могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией

* Сначала следует преобразовать плоскость общего положения в проецирующую, а затем — в плоскость уровня.