Прямая, перпендикулярная к плоскости. Теорема о проецировании прямого угла
Прямая, перпендикулярная к плоскости, перпендикулярна к любой прямой этой плоскости. На основании теоремы о проецировании прямого угла, а суть ее в следующем:
при прямоугольном проецировании прямой угол проецируется в натуральную величину (прямым) только в том случае, если одна из его сторон параллельна плоскости проекций, а другая — не перпендикулярна этой плоскости,
в качестве прямых плоскости общего положения удобнее всего использовать ее линии уровня.
Поэтому, проводя перпендикуляр к плоскости, необходимо брать в этой плоскости две такие прямые: горизонталь и фронталь.
Проекции прямой, перпендикулярной к плоскости, на комплексном чертеже перпендикулярны к соответствующим проекциям ее линий уровня, т.е. если прямая линия перпендикулярна плоскости, то ее горизонтальная проекция должна быть перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция — фронтальной проекции фронтали (рис. 67) или соответствующим следам плоскости (рис. 68).
На рис. 69 изображена плоскость общего положения a (a|| b), к которой к которой требуется провести перпендикулярную прямую.
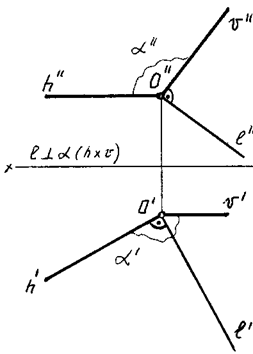  Рис. 67 Рис. 68 Рис. 67 Рис. 68 |

Рис. 69
Проводим в данной плоскости горизонталь h (через точки 1,3) и фронталь v (через точки 1,4) (рис. 69).
Затем из точки 1 проводим прямую n перпендикулярно к горизонтали и фронтали плоскости следующим образом:
n' ^ h' n'' ^ h''
Построенная прямая n (n', n'') является искомым перпендикуляром к плоскости a.
Перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Построение таких плоскостей может быть выполнено двумя путями:
1) плоскость проводится через перпендикуляр к другой;
2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.
На рис. 70 изображены прямая общего положения l и плоскость общего положения a (а ´ b). Требуется построить через прямую l плоскость, перпендикулярную к плоскости a.
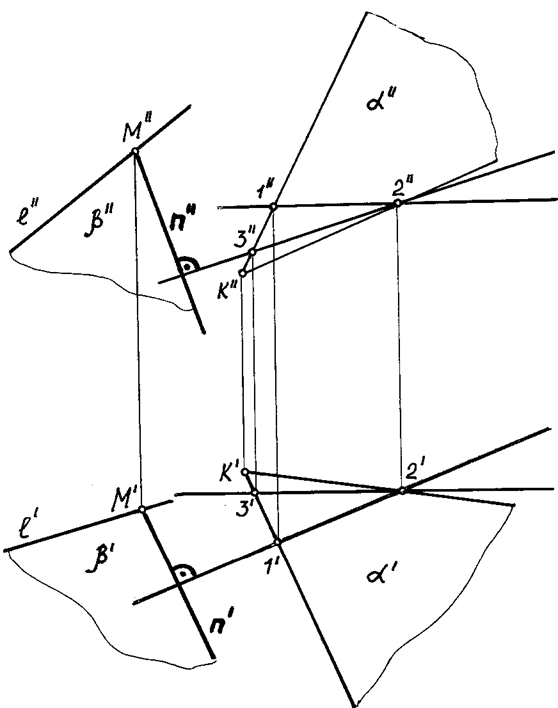
Рис. 70
Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости a, заданной пересекающимися прямыми a и b.
Проводим в плоскости a горизонталь h и фронталь v (рис. 70).
Далее из точки М, взятой на прямой l, опускаем перпендикуляр n, пользуясь рассмотренным выше положением: n' ^ h'; n'' ^ v'', т.е. горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная его проекция — перпендикулярна фронтальной проекции фронтали (рис. 70).
Плоскость b (l ´ n), проходящая через прямую n, будет перпендикулярна к плоскости a.
Перпендикулярные прямые
Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.
На рис. 71 изображена прямая l общего положения, к которой требуется провести перпендикулярную прямую.
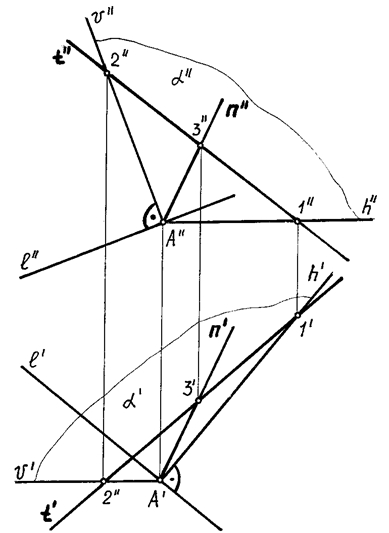
Рис. 71
Через точку А прямой l строим перпендикулярную к ней плоскость a (h ´ v):
l' ^ h'; l'' ^ h'' (рис. 71).
Любая прямая, лежащая в плоскости a будет также перпендикулярна к данной прямой l. Поэтому проведем в этой плоскости произвольную прямую t, на которой возьмем произвольную точку, например, точку В (рис. 71).
Соединив точки А и В, лежащие в плоскости , получим прямую n, перпендикулярную к данной прямой l (рис. 71).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1) Что называется линией наибольшего наклона плоскости?
