Умножение вероятностей

Учреждение образования «Белорусская государственная

Сельскохозяйственная академия»

Кафедра высшей математики

СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ

Конспект лекции для студентов бухгалтерского факультета

заочной формы получения образования (НИСПО)

Горки, 2013

Сложение и умножение вероятностей. Повторные

Независимые испытания

Сложение вероятностей

Суммой двух совместных событий А и В называется событие С, состоящее в наступлении хотя бы одного из событий А или В. Аналогично суммой нескольких совместных событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

Суммой двух несовместных событий А и В называется событие С, состоящее в наступлении или события А, или события В. Аналогично суммой нескольких несовместных событий называется событие, состоящее в наступлении какого-либо одного из этих событий.

Справедлива теорема сложения вероятностей несовместных событий: вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. 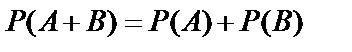. Эту теорему можно распространить на любое конечное число несовместных событий.

Из данной теоремы следует:

сумма вероятностей событий, образующих полную группу, равна единице;

сумма вероятностей противоположных событий равна единице, т.е. .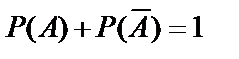

Пример 1. В ящике находятся 2 белых, 3 красных и 5 синих шара. Шары перемешивают и наугад извлекают один. Какова вероятность того, что шар окажется цветным?

Решение. Обозначим события:

A={извлечён цветной шар};

B={извлечён белый шар};

C={извлечён красный шар};

D={извлечён синий шар}.

Тогда A=C+D. Так как события C, D несовместны, то воспользуемся теоремой сложения вероятностей несовместных событий: .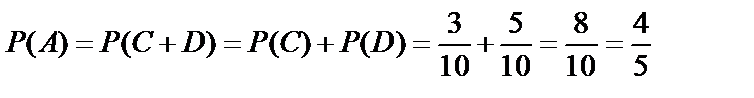

Пример 2. В урне находятся 4 белых шара и 6 – чёрных. Из урны наугад вынимают 3 шара. Какова вероятность того, что все они одного цвета?

Решение. Обозначим события:

A={вынуты шары одного цвета};

B={вынуты шары белого цвета};

C={вынуты шары чёрного цвета}.

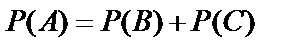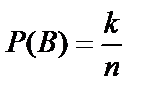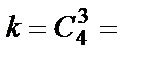Так как A=B+C и события В и С несовместны, то по теореме сложения вероятностей несовместных событий . Вероятность события В равна , где 4,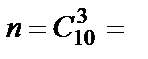

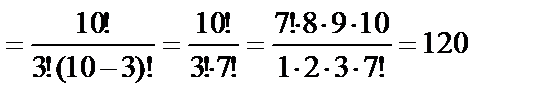. Подставим k и n в формулу и получим 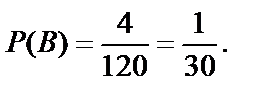Аналогично найдём вероятность события С: 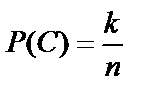, где 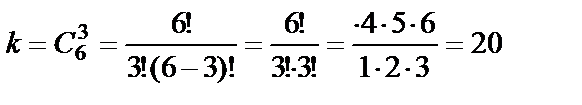, , 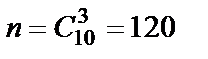т.е. 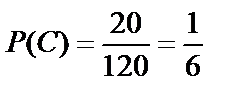. Тогда .

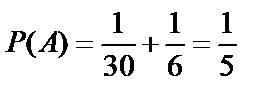Пример 3. Из колоды в 36 карт наугад вынимают 4 карты. Найти вероятность того, что среди них окажется не менее трёх тузов.

Решение. Обозначим события:

A={среди вынутых карт не менее трёх тузов};

B={среди вынутых карт три туза};

C={среди вынутых карт четыре туза}.

Так как A=B+C, а события В и С несовместны, то 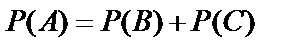. Найдём вероятности событий В и С:

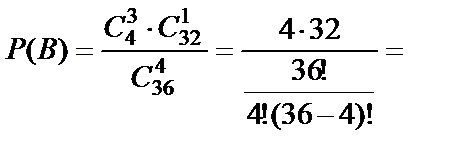
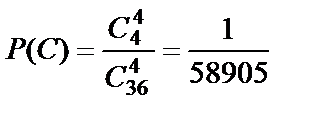, . Следовательно, вероятность того, что среди вынутых карт не менее трёх тузов, равна

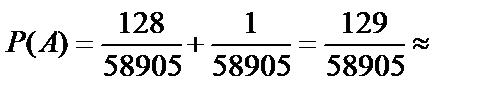0.0022.

Умножение вероятностей

Произведением двух событий А и В называется событие С, состоящее в совместном наступлении этих событий: 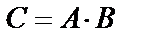. Это определение распространяется на любое конечное число событий.

Два события называются независимыми, если вероятность наступления одного из них не зависит от того, произошло другое событие или нет. События 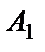, , 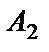… , 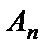называются независимыми в совокупности, если вероятность наступления каждого из них не зависит от того, произошли или не произошли другие события.

Пример 4. Два стрелка стреляют по цели. Обозначим события:

A={первый стрелок попал в цель};

B={второй стрелок попал в цель}.

Очевидно, что вероятность попадания в цель первым стрелком не зависит от того, попал или не попал второй стрелок, и наоборот. Следовательно, события А и В независимы.

Справедлива теорема умножения вероятностей независимых событий: вероятность произведения двух независимых событий равна произведению вероятностей этих событий: .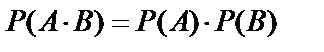

Эта теорема справедлива и для n независимых в совокупности событий: .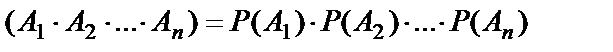

Пример 5. Два стрелка стреляют по одной цели. Вероятность попадания первого стрелка равна 0.9, а второго – 0.7. Оба стрелка одновременно делают по одному выстрелу. Определить вероятность того, что будут иметь место два попадания в цель.

Решение. Обозначим события:

A={первый стрелок попадёт в цель};

B={второй стрелок попадёт в цель};

C={оба стрелка попадут в цель}.

Так как 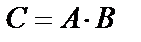, а события А и В независимы, то 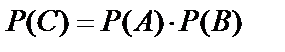, т.е. .

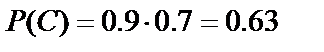События А и В называются зависимыми, если вероятность наступления одного из них зависит от того, наступило другое событие или нет. Вероятность наступления события А при условии, что событие В уже наступило, называется условной вероятностью и обозначается 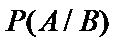или .

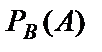Пример 6. В урне находятся 4 белых и 7 чёрных шаров. Из урны извлекаются шары. Обозначим события:

A={извлечён белый шар} ;

B={извлечён чёрный шар}.

Перед началом извлечения шаров из урны 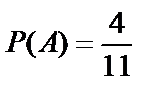. Из урны извлекли один шар и он оказался чёрным. Тогда вероятность события А после наступления события В будет уже другой, равной 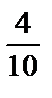. Это означает, что вероятность события А зависит от события В, т.е. эти события будут зависимыми.

Справедлива теорема умножения вероятностей зависимых событий: вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило, т.е. 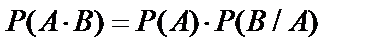или .

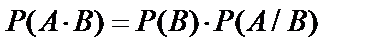Пример 7. В урне находятся 4 белых шара и 8 красных. Из неё наугад последовательно извлекают два шара. Найти вероятность того, что оба шара будут чёрными.

Решение. Обозначим события:

A={первым извлечён чёрный шар};

B={вторым извлечён чёрный шар}.

События А и В зависимы, так как 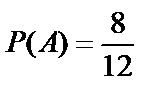, а 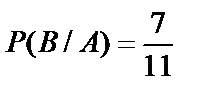. Тогда .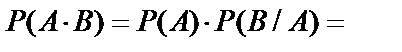

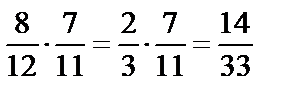Пример 8. Три стрелка стреляют по цели независимо друг от друга. Вероятность попадания в цель для первого стрелка равна 0.5, для второго – 0.6 и для третьего – 0.8. Найти вероятность того, что произойдут два попадания в цель, если каждый стрелок сделает по одному выстрелу.

Решение. Обозначим события:

A={произойдут два попадания в цель};

B={первый стрелок попадёт в цель};

C={второй стрелок попадёт в цель};

D={третий стрелок попадёт в цель};

={первый стрелок не попадёт в цель};

={второй стрелок не попадёт в цель};

={третий стрелок не попадёт в цель}.

По условию примера , , ,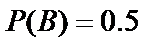

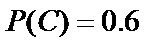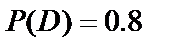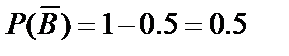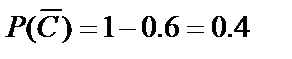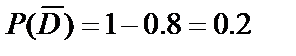, , . Так как 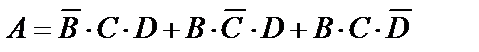, то используя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим:

.

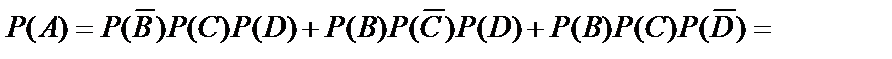
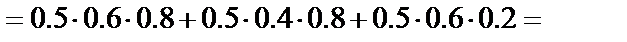
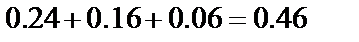Пусть события 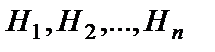образуют полную группу событий некоторого испытания, а событии А может наступить только с одним из этих событий. Если известны вероятности 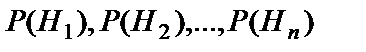и условные вероятности 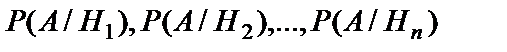события А, то вероятность события А вычисляется по формуле:

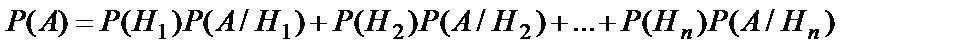или 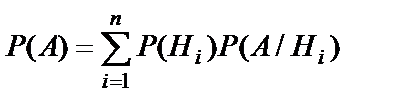. Эта формула называется формулой полной вероятности, а события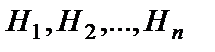 гипотезами.

Пример 9. На сборочный конвейер поступает 700 деталей с первого станка и 300 деталей со второго. Первый станок даёт 0.5% брака, а второй – 0.7%. Найти вероятность того, что взятая деталь будет бракованной.

Решение. Обозначим события:

A={взятая деталь будет бракованной};

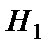={деталь изготовлена на первом станке};

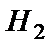={деталь изготовлена на втором станке}.

Вероятность того, что деталь изготовлена на первом станке, равна 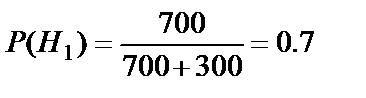. Для второго станка 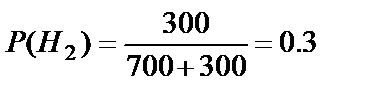. По условию вероятность получения бракованной детали, изготовленной на первом станке, равна 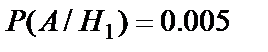. Для второго станка эта вероятность равна 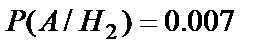. Тогда вероятность того, что взятая деталь будет бракованной, вычисляется по формуле полной вероятности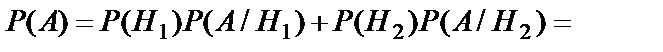

.

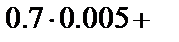
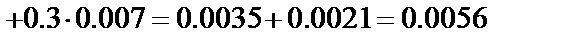Если известно, что в результате испытания наступило некоторое событие А, то вероятность того, что это событие наступило с гипотезой 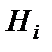, равна 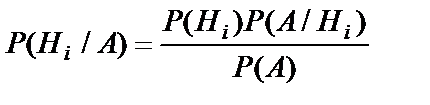, где 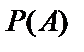- полная вероятность события А. Эта формула называется формулой Байеса и позволяет вычислять вероятности событий 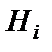после того, как стало известно, что событие А уже наступило.

Пример 10. Однотипные детали к автомобилям производятся на двух заводах и поступают в магазин. Первый завод производит 80% общего количества деталей, а второй – 20%. Продукция первого завода содержит 90% стандартных деталей, а второго – 95%. Покупатель купил одну деталь и она оказалась стандартной. Найти вероятность того, что эта деталь изготовлена на втором заводе.

Решение. Обозначим события:

A={куплена стандартная деталь};

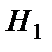={деталь изготовлена на первом заводе};

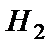={деталь изготовлена на втором заводе}.

По условию примера 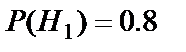, , 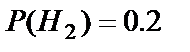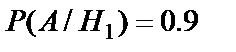и 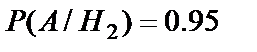. Вычислим полную вероятность события А: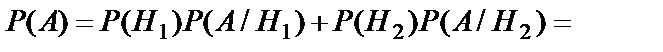 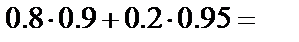0.91. Вероятность того, что деталь изготовлена на втором заводе, вычислим по формуле Байеса: .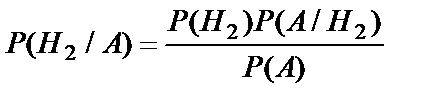

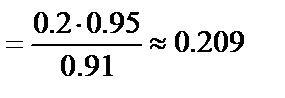Формула Бернулли

Испытания называются независимыми, если при каждом из них событие А наступает с одной и той же вероятностью 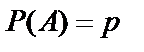, не зависящей от того, наступило или не наступило это событие в других испытаниях. Вероятность противоположного события 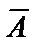в этом случае равна .

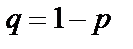Пример 11. Бросается игральный кубик n раз. Обозначим событие A={выпадение трёх очков}. Вероятность наступления события А в каждом испытании равна 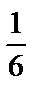и не зависит от того, наступило или не наступило это событие в других испытаниях. Поэтому эти испытания являются независимыми. Вероятность противоположного события 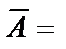{не выпадение трёх очков} равна .

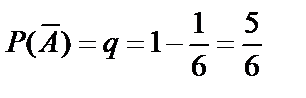Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события А равна p, событие наступит ровно k раз (безразлично в какой последовательности), вычисляется по формул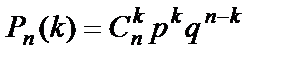е , где 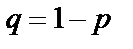. Эта формула называется формулой Бернулли и удобна она в том случае, если число испытаний n не слишком велико.

Пример 12. Доля плодов, заражённых болезнью в скрытой форме, составляет 25%. Случайным образом отбирается 6 плодов. Найти вероятность того, что среди выбранных окажется: а) ровно 3 заражённых плода; б) не более двух заражённых плодов.

Решение. По условию примера .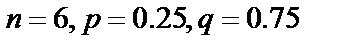

а) По формуле Бернулли вероятность того, что среди шести отобранных плодов заражёнными окажутся ровно три, равна

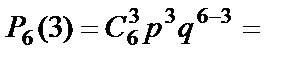
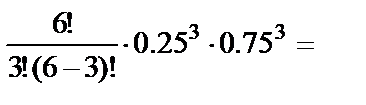
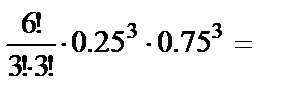
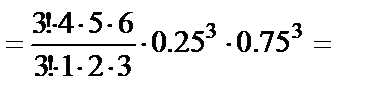
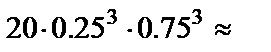0.132.

б) Обозначим событие A={заражённых будет не более двух плодов}. Тогда 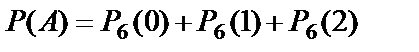. По формуле Бернулли:

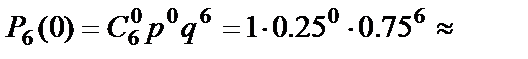0.178;

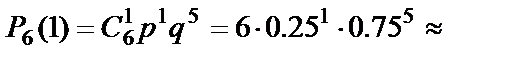0.356;

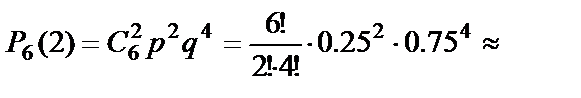0.297.

Следовательно, 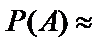0.178+0.356+0.297=0.831.

Теоремы Лапласа

По формуле Бернулли находится вероятность того, что событие А наступит k раз в n независимых испытаниях и в каждом испытании вероятность события А постоянна. При больших значениях n вычисления по формуле Бернулли становятся трудоёмкими. В этом случае для вычисления вероятности события А целесообразнее использовать другую формулу.

Локальная теорема Лапласа. Пусть вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы. Тогда вероятность того, что событие А наступит ровно k раз при достаточно большом числе n испытаний, вычисляется по формуле

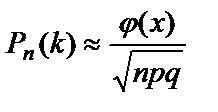, где 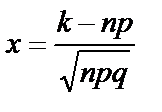, а значения функции 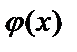приведены в таблице.

Основными свойствами функции 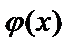являются:

Функция 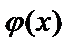определена и непрерывна в интервале .

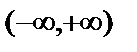Функция 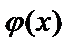положительна, т.е. 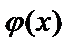>0.

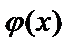Функция чётная, т.е. .

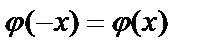Так как функция 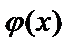чётная, то в таблице приведены её значения только для положительных значений х.

Пример 13. Всхожесть семян пшеницы составляет 80%. Для опыта отбирается 100 семян. Найти вероятность того, что из отобранных семян взойдут ровно 90.

Решение. По условию примера n=100, k=90, p=0.8, q=1-0.8=0.2. Тогда 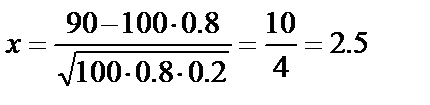. По таблице найдём значение функции 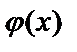: 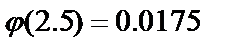. Вероятность того, что из отобранных семян взойдут ровно 90, равна 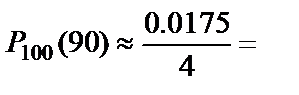0.0044.

При решении практических задач возникает необходимость найти вероятность наступления события А при n независимых испытаниях не менее 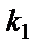раз и не более 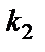раз. Такая задача решается с помощью интегральной теоремы Лапласа: Пусть вероятность p наступления события А в каждом из n независимых испытаний постоянна и отлична от нуля и единицы. Тогда вероятность того, что событие наступит не менее 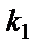раз и не более 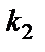раз при достаточно большом числе испытаний, вычисляется по формуле

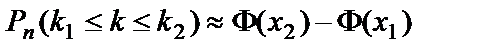, где , .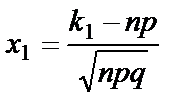

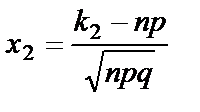Функция 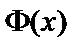называется функцией Лапласа и не выражается через элементарные функции. Значения этой функции приведены в специальных таблицах.

Основными свойствами функции 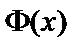являются:

.

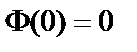Функция возрастает в интервале .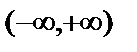

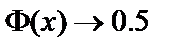при .

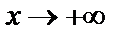Функция 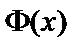нечётная, т.е. .

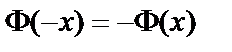Пример 14. Предприятие выпускает продукцию, из которой 13% не высшего качества. Определить вероятность того, что в непроверенной партии из 150 единиц продукции высшего качества будет не менее 125 и не более 135.

Решение. Обозначим 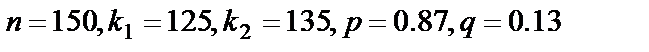. Вычислим ,

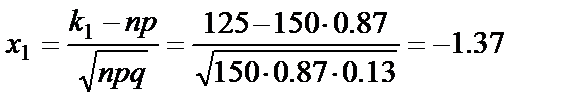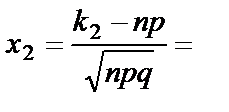
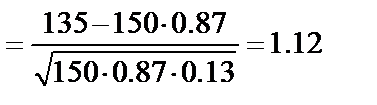. Тогда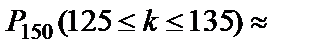

.
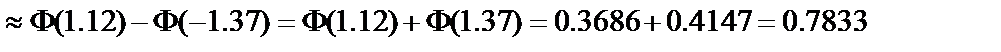