Дополнительные задачи для 5-го класса

(математическое моделирование)

(Берник В. И.)

1. Фермер решил оградить забором прямоугольный участок земли площадью 72 м2. Какой будет длина этого забора, если в длину участок в два раза больше, чем в ширину? (Ответ: 36 метров)

2. Подводящая труба может наполнить бассейн за 15 часов, а отводящая труба может выпустить всю воду из бассейна за 10 часов. Когда бассейн был полон, по ошибке начали работать обе трубы. Через сколько часов бассейн будет пуст? (Ответ: через 30 часов)

3. На сковородке помещается 2 драника. На поджаривание драника с одной стороны уходит 1 мин. Поджарьте 3 драника за 3 минуты. (Ответ: обозначим драники числами 1, 2 и 3, а их разные половинки буквами а и б. На протяжении первой минуты жарим 1а и 2а. На протяжении второй – 1б и 3а. За третью минуту жарим 2б и 3б. Драники поджарены)

4. Докажите, что за 15 мин. можно поджарить 15 драников. (Ответ: первые 12 драников жарим по два за 12 минут. Остальные три жарим как в задаче 7)Другое решение?

5. Лифт поднимается на шестой этаж за 30 секнуд. За сколько секунд он поднимается на 11 этаж? (Ответ: 60 секунд)

6. На шахматном турнире каждый участник играет со всеми другими. Сколько было участников, если сыграли 28 партий? (Ответ: 8 участников)

7. Все страницы книги пронумерованы цифрами от первой до последней. Использовано 810 цифр. Сколько страниц в книге? (Ответ: 306 страниц)

8. На участке дороги длиной 1,5 км. разрешена скорость 40 км/ч. Водитель проехал этот участок за 2 мин. Нарушил ли он правила? (Ответ: водитель нарушил правила)

9. Поезд длиной 1 км. въезжает в тоннель, длина которого 1 км. Скорость поезда 60 км/ч. За какое время поезд полностью пройдет тоннель? (Ответ: 2 минуты)

10. Во сколько раз секундная стрелка движется быстрее минутной, а минутная – часовой? (Ответ: в 60 и 12 раз)

11. Как при помощи чашечных весов без гирь разделить 24 кг на две части – 9 и 15 кг (Ответ: делим 24 на 12 и 12, затем 12 на 6 и 6 и 6 разделим на 3 и 3. Таким образом 24 кг мы разделили на части 12 кг 6 кг 3 кг 3 кг. Из 6 и 3 соствим 9 из 12 и 3 составим 15)

12. Как с помощью 7-литрового ведра и 3-литровой банки налить в кастрюлю 5 литров воды? (Ответ: выльем из полного ведра две банки, оставшийся литр выльем в кастрюлю, таким же способом дольем в кастрюлю еще 1 л. после чего дольем полную банку))

13. Миша пошел в первый класс в 2014 году. В какой класс он пойдет в 2022 году? (Ответ: 9 класс)

14. Есть 5 различных портфелей и связка из 5 разных ключей к ним. За какое наименьшее количество проб мы гарантированно откроем каждый портфель? (Ответ: 10)

15. Имеется несколько монет, одна из которых легче других и чашечные весы. Как найти ее за одно взвешивание, если у вас 3 монеты (Ответ: взвесить любые 2 монеты, если они равны, то легкая третья)

16. Найдите более легкую монету за не более чем 2 взвешивания, если у вас 9 монет (Ответ: поделим монеты на три группы по три монеты. Взвесив две группы мы определим, в какой группе легкая монета. В группе с легкой монетой взвесим две любые монеты что и позволит найти искомую монету)

17. Имеется кусок металла весом 4 кг. Какие две гири надо из него сделать, чтобы можно было взвесить на чашечных весах любой груз от 1 до 4 килограммов? (гири можно класть на обе чаши весов) (Ответ: 1 кг и 3 кг.).

18. На чашечных весах груз кладется на одну чашу весов, а гири на другую. Какие три гири надо сделать из куска металла 7 кг., чтобы можно было взвесить любой груз весом от 1 до 7 килограммов? (Ответ: 1 кг, 2 кг, 4 кг.)

19. Как взвесить слона, если у вас есть большая лодка, большая куча песка и весы, на которых можно взвешивать грузы до 100 кг? (Ответ: ввести в лодку слона и посмотреть на сколько она погружается в воду. Затем вывести слона и насыпать в лодку песка, чтобы лодка погрузилась в воду до той же отметки. Осталось взвесить песок из лодки на весах (по частям))

20. *Скорость двух пешеходов 4 км/ч и 6 км/ч. Они вышли навстречу друг другу из Минска и Самохвалович из точек, расстояние между которыми 20 км. Одновременно с первым навстречу второму выбежала собака со скоростью 20 км/ч. Добежав до второго пешехода она развернулась и побежала обратно до встречи с первым. При встрече с первым снова развернулась и побежала навстречу второму и так далее, пока пешеходы не встретились. Какое расстояние пробежала собака? (Ответ: 40 км).

21. Летние олимпийские игры проводятся в високосные годы, т. к. годы нацело делящиеся на 4, а зимние в четные годы, не делящиеся на 4. Пользуясь признаком делимости на 4 устно определите какие олимпийские игры пройдут в 2056, 2078, 2091 годах. (Ответ: в 2056- летние, в 2078-зимние, в 2091- игры не проводились)

22. Лимоны в корзинке пересчитали по 5, осталось 2. Затем по 7 лимонов – вновь осталось 2. В корзине было не более 50 лимонов. Назовите точное количество лимонов в корзине. Измениться ли ответ, если бы в корзине было не более 120 лимонов? (Ответ: 37 в первой задаче и 37, 72, 107 во второй)

23. Несколько человек купили подарок, внеся разные суммы. Как быстро сделать так, чтобы вклады каждого стали одинаковыми? (Ответ: стоимость подарка надо разделить на количество людей, а потом до этой стоимости доплатить тем, кто внёс меньший вклад, и раздать внёсшим большие вклады.)

24. Больной должен принимать две таблетки разных лекарств утром и вечером. Четыре имеющиеся таблетки, с виду неотличимые, смешались. Можно ли принять лекарства, не нарушив рекомендации врача. (Ответ: можно. Надо каждую таблетку поделить пополам, обозначив половинки a и b. Утром выпить 4 половинки a, вечером — 4 половинки b.).

25. Мы можем за один разрез разделить яблоко 2 части, за разреза на 3 части, за 3 разреза на 6 частей. За какое минимальное число разрезов можно разделить 5 яблок на 6 человек. (Ответ: 7 разрезов)

26. Имеются груз, гиря весом 1 килограмм и шар способный поднять 3 килограмма. Как определить тяжелее ли груз 2 килограмм (Ответ: привязать к шару груз и и гирю и посмотреть взлетит или нет)

27. Один прыжок кузнечика равен 1 метр. Сможет ли он допрыгать до другого кузнечика на расстояние 4 метра и вернутся в начальную точку за а) 7 прыжков; б) 8 прыжков; в) 9 прыжков (Ответ: а) нет; б) да; в) да)

28. Имеется два растения и три одинаковых мешка. В одном из них ядохимикат, а в двух других удобрение. При внесении удобрения рост растения значительно увеличивается, а при внесении ядохимиката растение чахнет. Как за одно внесение содержимого мешков каждому растению определить, где удобрение, а где ядохимикат. (Ответ: внести двум растениям содержимое двух разных мешков. Если оба начнут расти, значит, яд в третьем мешке. Если одно из них начнет чахнуть, то яд в том мешке, из которого вносили содержимое для этого растения)

29. Предыдущая задача в случае 3 растений и 7 мешков. (Ответ: для первого растения вносим порцию из 1, 2, 3 и 5 мешка, для второго растения вносим порцию из 1, 2, 4 и 6 мешка, для третьего вносим порцию из 1, 3, 4 и 6 мешка. При таком распределении содержимого мешков для растений, возможны 7 вариантов состояния этих растений, каждый из которых укажет на мешок с ядом:

Состояние 1 растения	Состояние 2 растения	Состояние 3 растения	Номер мешка с ядом
Выросло недостаточно или зачахло совсем	Выросло недостаточно или зачахло совсем	Выросло недостаточно или зачахло совсем
Выросло недостаточно или зачахло совсем	Выросло недостаточно или зачахло совсем	Выросло и выглядит здоровым
Выросло недостаточно или зачахло совсем	Выросло и выглядит здоровым	Выросло недостаточно или зачахло совсем
Выросло и выглядит здоровым	Выросло недостаточно или зачахло совсем	Выросло недостаточно или зачахло совсем
Выросло недостаточно или зачахло совсем	Выросло и выглядит здоровым	Выросло и выглядит здоровым
Выросло и выглядит здоровым	Выросло недостаточно или зачахло совсем	Выросло и выглядит здоровым
Выросло и выглядит здоровым	Выросло и выглядит здоровым	Выросло недостаточно или зачахло совсем

т. к. в каком-то из мешков яд точно есть, то все растения выглядеть здоровыми одновременно не могут).

30. *Две точки А и В начинают одновременно сближаться по меньшей дуге окружности, равной 150 м, и встречаются через 10 с. Если же точки начнут двигаться по большей дуге, то они встретятся через 14 с. Найдите длину окружности и скорости движения точек, если точка А может пройти всю окружность за время, за которое точка В пройдет 90 м. (Ответ: 360 м, 8 м/с, 2 м/с).

31. *Два автомобиля, двигаясь по кольцевой дороге с постоян­ными скоростями в одном направлении, оказываются рядом через каждые 3 ч. При движении с теми же скоростями в противоположных направлениях автомобили встречаются через каждые 20 мин. За какое время проедет всю коль­цевую трассу каждый автомобиль? (Ответ: 36 и 45 мин)

32. *Фрукты в магазин были доставлены двумя машинами, по 60 ящиков в каждой; при этом в 21 ящике были груши, а в остальных — яблоки. Сколько ящиков с грушами было в каждой машине, если известно, что в первой машине на один ящик с грушами приходилось в 3 раза больше ящиков с яблоками, чем во второй? (Ответ: 15 и 6).

33. *Сейчас 12 часов дня. Через какое время минутная стрелка снова сойдется с часовой? (Ответ: 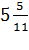мин.)

34. *На дороге расположены три магазина. Где следует построить логистический центр, чтобы сумма расстояний от него до всех магазинов была минимальной? (Ответ около среднего магазина)

35. *На дороге расположены четыре магазина. Где следует построить логистический центр, чтобы сумма расстояний от него до всех магазинов была минимальной? (Ответ: в любом месте между двумя не крайними магазинами)