Свойства тела Кельвина
Реологические свойства мягких биологических тканей. Реологические диаграммы.
К мягким тканям относятся практически все ткани нашего тела, кроме костной ткани (кожа, мышцы, сердце, мозг, легкие, печень, почки и т.д.). Свойства этих тканей сильно различны. Для того чтобы описать эти свойства на качественном и понятном уровне, используются простые скалярные соотношения.
Рассмотрим полоску длины 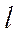 , на которую действует сила
, на которую действует сила 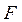 . Под действием этой силы полоска растягивается на величину
. Под действием этой силы полоска растягивается на величину 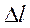 . По определению величина механического напряжения равна:
. По определению величина механического напряжения равна:
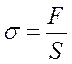
а величина удлинения равна:
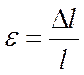
Для большого класса материалов величина напряжения пропорциональна удлинению:
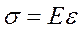
Коэффициент пропорциональности 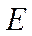 называется модулем Юнга.
называется модулем Юнга.
Тела, для которых наблюдается линейная зависимость 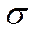 от
от 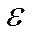 , называются линейными телами Гука.
, называются линейными телами Гука.
Для линейно-вязких тел наблюдается линейная зависимость 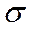 от
от 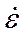 :
:
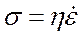
где 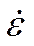 - скорость деформации,
- скорость деформации, 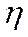 - вязкость тела,
- вязкость тела, 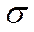 - напряжение сдвига.
- напряжение сдвига.
Такое тело называется мягким вязким телом или телом Ньютона.
Для того чтобы представить эти тела графически, используют реологические диаграммы.
Тело Гука представляется в виде пружинки
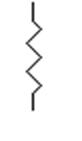
а реологическая диаграмма для тела Ньютона – амортизатор
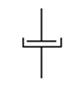
С помощью этих реологических диаграмм можно описать основные свойства биологических тканей – свойства упругости и мягкости.
На основе этих диаграмм можно конструировать самые разные тела.
1) параллельное соединение вязкого и упругого тел - тело Фойхта.
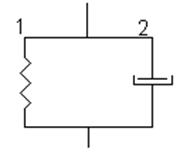
В этом случае для каждого элемента удлинение будет одинаково, а общая величина силы будет равна сумме двух сил.
Тогда имеем:
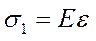
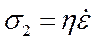
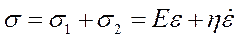
Это тело ведет себя как упругое, когда 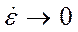 , и как вязкое, когда
, и как вязкое, когда 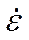 велико. Таким образом, это вязкоупругое тело.
велико. Таким образом, это вязкоупругое тело.
2) последовательное соединение вязкого и упругого тел
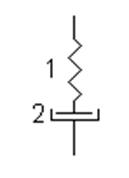
В этом случае сила, приложенная к обоим элементам, будет одинаковая, а общее удлинение будет равно сумме удлинения каждого отдельного элемента.
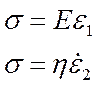
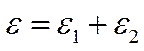
Тогда 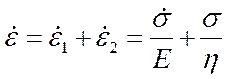
Такое тело ведет себя следующим образом: если к нему приложить какое-то напряжение, оно будет течь бесконечно долго. То есть это тело представляет собой вязкоупругую жидкость. Такое тело называется телом Максвелла.
3) вязкое и упругое тела соединены следующим образом:
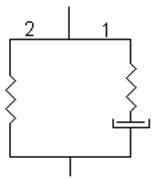
Такое тело называется телом Кельвина.Это тело используетсядля описания мягких биологических тканей.
Реологическое соотношение для тела Кельвина имеет следующий вид:
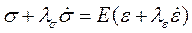
Коэффициенты 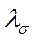 ,
, 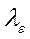 и
и 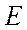 выражаются через
выражаются через 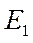 ,
, 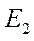 и
и 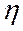 ;
;
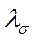 и
и 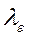 имеют размерность времени.
имеют размерность времени.
Такого же вида уравнение можно получить и с помощью другой диаграммы:
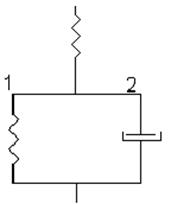
Но в этом случае связь 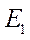 ,
, 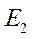 и
и 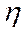 с
с 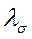 и
и 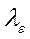 будет другой.
будет другой.
Свойства тела Кельвина
Релаксация напряжения
В эксперименте берем полоску, растягиваем до определенной длины и держим растянутой до этой длины.
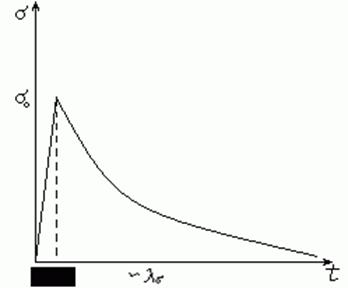
В ходе растяжения полоски величина напряжения резко возрастает до какой-то величины 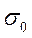 , а затем начинает спадать. Это снижение напряжения называется релаксацией напряжения. Явление хорошо описывается уравнением
, а затем начинает спадать. Это снижение напряжения называется релаксацией напряжения. Явление хорошо описывается уравнением
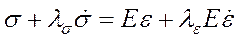
В этом случае последнее слагаемое в правой части равно 0, и происходит динамический процесс снижения напряжения 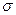 с характерным временем
с характерным временем 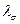 .
.
Свойство релаксации напряжения различно для разных тканей, и в некоторых тканях выражено очень сильно. Например, в гладких мышцах напряжение релаксирует почти до нуля и само значение 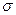 изменяется в 100-1000 раз за время порядка часов. Таким образом, гладкие мышцы приспосабливаются к деформации.
изменяется в 100-1000 раз за время порядка часов. Таким образом, гладкие мышцы приспосабливаются к деформации.
2) Ползучесть (creep)
Берем такую же полоску и привешиваем к ней грузик. При постоянной нагрузке в реологическом соотношении для тела Кельвина 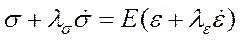
второе слагаемой в левой части равно нулю. Тогда зависимость удлинения от времени имеет следующий вид:



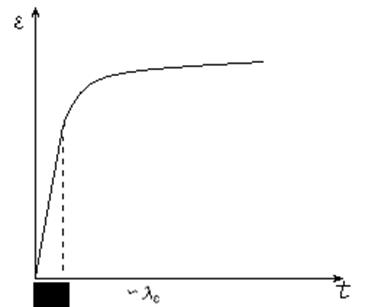
Видно, что тело начинает течь и постепенно «притекает» к некоторой величине деформации. Такое свойство биологических мягких тканей называется текучестью. Конечное значение деформации определяется коэффициентом упругости 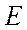 , а характерное время течения – это время
, а характерное время течения – это время 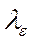 .
.
