Шаг 1.Определение потенциалов поставщиков и потребителей.
Задание № 2.
На трех базах А1, А2, А3 находится однородный груз в количестве 200, 200 и 100 т. Этот груз необходимо развезти пяти потребителям В1, В2, В3, В4, В5, потребности которых в данном грузе составляют 70, 80, 150, 110 и 90 т соответственно. Стоимость перевозок пропорциональна расстоянию и количеству перевозимого груза. Матрица тарифов имеет вид:
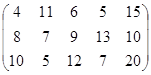
Спланировать перевозки так, чтобы их общая стоимость была минимальной.
Решение.
Составим транспортную таблицу по условиям задачи:
  ПН ПО ПН ПО | В1 | В2 | В3 | В4 | В5 | Запасы аi |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребнос- ти bj |
Строки таблицы соответствуют базам (пунктам отправления, ПО), а столбцы – заказчикам (пунктам назначения, ПН). Каждая клетка на пересечении некоторого столбца и какой-либо строки соответствует одному маршруту перевозок (например, клетка на пересечении А2 и В3 отвечает маршруту с базы А2 заказчику В3). Тарифы перевозок указаны в правом верхнем углу каждой клетки.
Решение транспортной задачи проводится в два этапа. На первом этапе находится первоначальный опорный план. На втором этапе на базе опорного плана методом потенциалов определяется оптимальный план.
На первом этапе рекомендуется подготовить первоначальный опорный план тремя разными методами: методом северо-западного угла, методом минимальной стоимости и методом двойного предпочтения. Затем из этих трех планов выбирается самый выгодный. Его и подвергают процедуре дальнейшей оптимизации методом потенциалов.
Рассмотрим метод северо-западного угла, или диагональный метод. В этом методе заполнение транспортной таблицы всегда начинается с клетки (А1 , В1), т.е. “северо-западного угла” таблицы. Далее, заполнение идет вокруг диагонали таблицы и всегда заканчивается в правом нижнем углу (клетка ( А3 , В5 )). В каждой клетке объем перевозки определяется как наименьшее значение из двух чисел: остатка запаса на базе и остатка заявки потребителя. Отсюда:
х11 = min { a1 , b1 } = { 200 ; 70 } = 70.
Таким образом, заявка первого потребителя выполняется в полном объеме, поскольку на базе имелся больший запас товара. Поэтому остальные клетки первого столбца не нужны и остаются пустыми.
Далее наступает очередь второго заказчика, который со своей заявкой приходит на первую базу, где еще остался товар:
х12 = min { 200 - 70 ; 80 } = { 130 ; 80 } = 80.
Он также получает всё, и остальные клетки второго столбца также будут пустыми.
Теперь на первой базе осталось только 50 т груза. Поэтому третий заказчик получит только эти 50 т, хотя ему требуется 150 т.
х13 = min { 200 – 70 – 80 ; 150} = 50.
Поскольку на первой базе больше не осталось товара, остальные клетки первой строки будут пустыми.
Остальную часть своего заказа второй заказчик получит на второй базе:
х23 = min { 200 ; 150 – 50 } = 100.
Далее поцесс повторяется для остальных заказчиков, в результате чего получаем опорный план:
  ПН ПО ПН ПО | В1 | В2 | В3 | В4 | В5 | аi |
| А1 | ¾ | ¾ | ||||
| А2 | ¾ | ¾ | ||||
| А3 | ¾ | ¾ | ¾ | |||
| bj |
В этом опорном плане семь занятых клеток. Поскольку их должно быть m +n –1, где m – число баз, n - число заказчиков, план является невырожденным. Если бы клеток было меньше, чем m +n –1, план был бы вырожденным.
Осталось подсчитать общую стоимость перевозок. Она складывается из произведений объемов перевозок и тарифов по всем занятым клеткам, т.е.:
F ( X1 ) = 70 × 4 + 80 × 11 + 50 × 5 + 100 × 9 + 100 × 13 + 10 × 7 + 90 × 20 = 5530.
Как видим, при распределении грузов совсем не учитывается стоимость перевозок. Поэтому, как правило, метод северо-западного угла дает опорный план, далекий от оптимального.
Построим опорный план методом минимальной стоимости (или минимального элемента). Суть метода в следующем. Сначала из всей таблицы выбираем клетку с самым маленьким тарифом. В эту клетку помещаем максимально возможную перевозку, а затем вычеркиваем клетки, ставшие ненужными. Затем в оставшейся части таблицы процесс повторяем, пока вся таблица не будет заполнена.
В данном случае сама дешёвая клетка ( А1 , В1 ). С неё и начинаем распределение грузов:
х11 = min { 200 ; 70 } = 70.
Вычеркиваем оставшиеся клетки первого столбца и повторяем процесс в оставшейся части таблицы. Запишем последовательность заполнения клеток:
х14 = min { 200 - 70 ; 110 } = 110;
х32 = min { 100 ; 80 } = 80;
х13 = min { 200 – 70 – 110 ; 150 } = 20;
х23 = min { 200 ; 150 - 20 } = 130;
х25 = min { 200 - 130 ; 90 } = 70;
х35 = 20.
Получаем следующий опорный план:
| ПН ПО | В1 | В2 | В3 | В4 | В5 | bj |
| А1 | ¾ | ¾ | ||||
| А2 | ¾ | ¾ | ¾ | |||
| А3 | ¾ | ¾ | ¾ | |||
| аi |
Здесь получены семь ненулевых перевозок, поэтому план невырожденный. Подсчитаем его стоимость:
F ( X2 ) = 4 × 70 + 6 × 20 + 5 × 110 + 9 × 130 + 10 × 70 + 5 × 80 + 20 × 20 = 3620.
Как видим, этот опорный план дешевле первого.
Теперь построим опорный план методом двойного предпочтения. При этом сначала в каждом столбце отметим галочкой клетку с наименьшей стоимостью, затем то же самое делаем с каждой строкой. Далее максимально возможные объемы перевозок помещаем в клетки, отмеченные двойной галочкой. Затем распределяем перевозки по клеткам, отмеченным одной галочкой. В оставшейся части таблицы перевозки распределяем по методу минимальной стоимости.
Как видим, данный метод фактически является модифицированным методом минимальной стоимости.
Очевидно, что по крайней мере одна клетка таблицы будет иметь двойную галочку (этой клеткой обязательно будет клетка с минимальным тарифом). В нашем случае таких клеток будет две: (А1, В1 ) и (А3, В2 ). Их и заполним в первую очередь:
х11 = 70 ; х32 =80.
Клетками с одной галочкой будут : (А1, В4 ) ; (А2, В5 ) ; (А2, В2 ) и (А1, В3 ) (проверьте это). Клетка (А2, В2 ) не будет заполнена, в этом нет необходимости, поскольку во втором столбце занята одна клетка : (А3, В2 ) с двойной галочкой. Остальные клетки используем:
х14 = 110 ; х13 = 20 ; х25 = 90.
Разумеется, после их заполнения ненужные клетки вычеркиваем. Оставшиеся две клетки галочек заполняем по минимальной стоимости:
х23 = 110 ; х33 =20.
 Получаем новый опорный план транспортной задачи:
Получаем новый опорный план транспортной задачи:
| ПН ПО | В1 | В2 | В3 | В4 | В5 | аi |
| А1 |   4 4 | ¾ |  6 6 |  5 5 | ¾ | |
| А2 | ¾ |  7 ¾ 7 ¾ | ¾ | 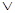 10 10 | ||
| А3 | ¾ | 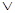 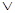 5 5 | ¾ | ¾ | ||
| bj |
Этому опорному плану соответствует стоимость перевозок:
F (X3) =4 × 70 + 6 × 20 + 5 × 110 + 10 × 90 + 5 × 80 + 12 × 20 = 3480.
Отметим, что и этот план имеет семь ненулевых перевозок, поэтому является невырожденным.
Как видим из сравнения планов, последний является самым дешевым, т.е. самым выгодным. Поэтому его берем в качестве основы для дальнейшей оптимизации по методу потенциалов.
Основой метода потенциалов является теорема о потенциалах. Её формулировка следующая:
План ( 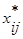 ) транспортной задачи является оптимальным тогда и только тогда, когда существуют числа такие ui (i =
) транспортной задачи является оптимальным тогда и только тогда, когда существуют числа такие ui (i = 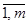 ), vj ( j =
), vj ( j = 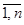 ), называемые соответственно потенциалами поставщиков и потребителей, при которых выполняются соотношения:
), называемые соответственно потенциалами поставщиков и потребителей, при которых выполняются соотношения:
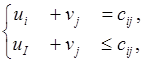
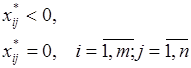 (11)
(11)
Как видим из системы (11), уравнения записываются для заполненных клеток, а неравенства – для свободных клеток. Справа везде стоят тарифы перевозок в соответствующих клетках.
На этой теореме основывается сам алгоритм оптимизации планов транспортной задачи, который называется методом потенциалов. Рассмотрим его подробно.
Шаг 1.Определение потенциалов поставщиков и потребителей.
На этом шаге составляем систему уравнений для потенциалов, используя только занятые клетки. Используем последний опорный план:
| ПН ПО | В1 v1=4 | В2 v2=-1 | В3 v3=6 | В4 v4=5 | В5 v5=7 | аi |
| А1 u1=0 | ¾ | ¾ | ||||
 А2 u2=3 А2 u2=3 | ¾ | ¾ | ¾ | |||
| А3 u3=6 | ¾ | ¾ | ¾ | |||
| bj |
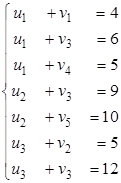
Заметим, что в этой системе всего 8 неизвестных, т.е. m + n (3 + 5). Однако уравнений всего 7, поскольку в невырожденном опорном плане всего 7 заполненных клеток
(т.е. m + n - 1 ). Для однозначного решения не хватает одного уравнения. В этом случае один из потенциалов, например, и1 (может быть и другой потенциал) приравнивают некоторому постоянному числу, например, нулю:
и1=0.
Это и будет недостающим уравненим в системе. Теперь систему можно легко решить, имея в виду, что все уравнения состоят только из двух неизвестных. Результаты решения записаны в заголовочных клетках таблицы. Решать систему можно и непосредственно по таблице, используя занятые клетки с известными значением одного из потенциалов. Этот процесс всегда можно начать с первой строки, где уже известно значение и1=0.
Сделаем замечание для случая, когда опорный план является вырожденным. В этом случае количество уравнений для определения потенциалов будет меньше, чем m + n – 1. Это недопустимо мало, поэтому используют следующий приём. В недостающее число свободных клеток записывают нулевые значения перевозок, а сами эти клетки считаются занятыми, и для них записывают уравнения потенциалов. Такая модификация опорного плана не влияет на его стоимость, поскольку нулевые перевозки имеют нулевые стоимости. Свободные клетки значащих нулей для подстановки выбираются не произвольно, однако об этом поговорим ниже.
Шаг 2. Проверка оптимальности опорного плана.
На этом шаге проверяем выполнение неравенств (11) для свободных клеток. Перепишем их в виде:
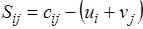 ,
, 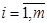 ;
; 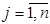 .
.
Если все Sij неотрицательны, значит, опорный план оптимален, и на этом наш вычислительный процесс заканчивается. Подсчитаем оценки для свободных клеток:
S12 = 11 – (0 - 1) = 12 ³ 0
S15 = 15 – (0 +7) = 8 ³ 0
S21 = 8 – (3 + 4) = 1 ³ 0
S22 = 7 – (3 - 1) = 5 ³ 0
S24 = 13 – (3 + 5) = 5 ³ 0
S31 = 10 – (6 + 4) = 0 ³ 0
S34 = 7 – (6 + 5) = - 4 < 0
S35 = 20 – (6 + 7) = 7 ³ 0
Оценка S34 оказалась отрицательной, значит, одно из неравенств (11) нарушено, и опорный план не является оптимальным . Таким образом, он нуждается в модификации, которую проведем на следующем этапе.
Шаг 3. Пересчет по циклу.
Для пересчета плана выбирается клетка, в которой оказалась отрицательная оценка. Таких клеток может оказаться несколько. В этом случае для пересчета выбирается клетка с самой отрицательной оценкой.
Циклом в опорном плане транспортной задачи называется замкнутый многоугольник из клеток таблицы с прямыми углами в вершинах, в который входят только вершинные клетки, и все эти клетки, кроме одной (для которой организуется пересчет, т.е. с отрицательной оценкой), являются занятыми.
 |
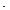 Таким образом, одна из клеток цикла является свободной. Циклы могут иметь бесконечно много конфигураций, например:
Таким образом, одна из клеток цикла является свободной. Циклы могут иметь бесконечно много конфигураций, например: В последнем случае место пересечения двух линий цикла не входит в сам цикл, поскольку в вершинах цикла, которые, собственно, только и входят в цикл, совершается поворот на 90 0.
Каждой вершине цикла присваивается знак плюс или минус. При этом начальная клетка цикла, котороя является свободной, имеет знак плюс. Остальные клетки имеют чередующиеся знаки. Поскольку очевидно, что любой цикл имеет четное число вершин, то количество отрицательных и положительных вершин всегда будет одинаковым.
В данном случае цикл пойдет через клетки (А3, В4 ) ; (А1, В4 ) ; (А1, В3 ) и (А3, В3 ). В таблице цикл обрисован пунктирным прямоугольником.
Одним из признаков опорного плана транспортной задачи является то обстоятельство, что для любой свободной клетки всегда можно построить замкнутый цикл, где все остальные вершины будут располагаться в занятых клетках. Однако такой цикл будет единственным. С другой стороны, в опорном плане нельзя построить замкнутый цикл, в который входили бы только занятые клетки. Это привело бы к противоречивой системе уравнений для потенциалов. Данное замечание подсказывает правило, по которому в вырожденный опорный план должны быть помещены значащие нули: их нельзя располагать в клетках, которые могут создать замкнутый цикл только из занятых клеток.
Отсюда следует, что, если в транспортной задаче число занятых клеток превышает m + n – 1, то из них можно построить замкнутый цикл, и план уже не будет опорным.
Теперь вернемся к построенному нами циклу. Из всех отрицательных вершин цикла выбираем наименьшее значение перевозок:
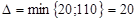
Далее на значение 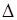 уменьшаем перевозки в отрицательных вершинах цикла, а во всех положительных вершинах значения перевозок увеличиваем на эту же величину. Поскольку в цикле чётное число вершин, то в пределах цикла общий объём перевозок не изменится, что не приведет к нарушению баланса между запасами и заявками. Пересчитанная таблица выглядит так:
уменьшаем перевозки в отрицательных вершинах цикла, а во всех положительных вершинах значения перевозок увеличиваем на эту же величину. Поскольку в цикле чётное число вершин, то в пределах цикла общий объём перевозок не изменится, что не приведет к нарушению баланса между запасами и заявками. Пересчитанная таблица выглядит так:
| ПН ПО | В1 v1=4 | В2 v2=3 | В3 v3=6 | В4 v4=5 | В5 v5=7 | аi |
| А1 u1=0 | ¾ | ¾ | ||||
| А2 u2=3 | ¾ | ¾ | ¾ | |||
| А3 u3=2 | ¾ | ¾ | ¾ | |||
| bj |
Пересчитаем стоимость нового плана:
F ( X4 ) = 4 × 70 + 6 × 40 + 5 × 90 + 9 × 110 + 10 × 90 + 5 × 80 + 7 × 20 = 3400.
Как видим, стоимость перевозок уменьшилась.
Шаг 4. Определение потенциалов в новом плане.
Этот шаг является повторением шага 1. Система уравнений здесь почти не отличается от предыдущей, кроме одного уравнения. Это связано с тем, что свободная клетка (А3, В4 ) стала занятой, а клетка (А3, В3) стала свободной. Фактически здесь идет речь о преобразовании однократного замещения, которое имело место в симплекс методе. Соответственно одно из уравнений для потенциалов заменяется другим. Запишем новую систему:

Решаем эту систему аналогично, результаты помещены в заголовочные клетки последней таблицы.
Шаг 5. Расчет оценок для свободных клеток.
Этот шаг повторяет шаг 2. Считаем оценки:
S12 = 11 – (0 + 3) = 8 ³ 0
S15 = 15 – (0 +7) = 8 ³ 0
S21 = 8 – (3 + 4) = 1 ³ 0
S22 = 7 – (3 + 3) = 1 ³ 0
S24 = 13 – (3 + 5) = 5 ³ 0
S31 = 10 – (2 + 4) = 4 ³ 0
S33 = 12 – (2 + 6) = 4 ³ 0
S35 = 20 – (2 + 7) =11 ³ 0
Поскольку все оценки свободных клеток неотрицательны, полученный план является оптимальным. В противном случае пришлось бы продолжать шаги 1-3 процесса до тех пор, пока не будет получен оптимальный план.
Запишем решение транспортной задачи:
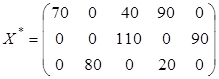
Fmin = F ( X* ) = 3400.
Задание № 3.
Торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, и получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров.
æ = 0,6
| Величины прибыли | ||||
| План продажи | Состояние спроса | |||
| П1 | П2 | П3 | П4 | |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 |
Решение. Задачи такого типа относятся к играм с природой (или статистическим играм). Любую хозяйственную деятельность человека можно рассматривать как игру с природой. Под “природой” понимается совокупность неопределенных факторов, влияющих на эффективность принимаемых решений. Но иногда мы располагаем некоторыми вероятностными характеристиками состояний природы.
Игра с природой отличается от матричной игры, в которой принимают участие два сознательных игрока, безразличием природы к выигрышу. Природа может даже помогать игроку. Такие игры в основном бывают двух типов: когда вероятности состояний природы неизвестны и когда они известны. От этого зависит метод решения игры.
Для решения игры с природой был предложен ряд критериев, ни один из которых не является универсальным, поскольку каждый из них основывается на своих специфических допущениях. Поэтому следует применять по очереди все эти критерии, причем каждый критерий дает свою рекомендацию относительно того, какое решение игрока является наилучшим. Если одна из стратегий (решений) игрока фигурирует в качестве лучшей чаще других, она в результате признается оптимальной.
Рассмотрим эти критерии подробнее.
1 случай. Вероятности состояний природы неизвестны.(варианты 1-5)
Максиминный критерий Вальда. С точки зрения этого критерия, игра с природой ведётся как игра с разумным, агрессивным противником, который всегда реализует самое невыгодное для игрока состояние. Это крайне пессимистический критерий. Здесь нужно рассчитывать на самый наихудший вариант, и поэтому при любой стратегии игрока ожидается, что выигрыш будет наименьшим. Поэтому из этих наименьших выигрышей по каждой стратегии выбирается наибольшее значение, которое гарантирует игроку хотя бы наименьший возможный выигрыш:
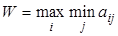 (12)
(12)
где аij – элемент матрицы выигрышей.
Сначала из каждой строки матрицы выбираем минимальный элемент, а затем среди полученных значений выбираем максимальное. Таким образом, получаем:
W = 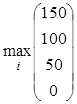 = 150,
= 150,
что соответствует стратегии А1. Таким образом, согласно критерию Вальда, наилучшей является стратегия А1, гарантирующая выигрыш, равный 150.
Критерий минимального риска Сэвиджа. Это также крайне пессимистический критерий, однако, в отличие от критерия Вальда, ориентируется не на выигрыш, а на риск проигрыша:
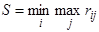 , (13)
, (13)
где rij – элемент матрицы рисков, которая получается из матрицы выигрышей по формуле:
rij = 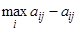
Матрица рисков имеет ту же размерность, что и матрица выигрышей, и формируется по столбцам матрицы выигрышей. В каждом столбце максимальный элемент заменяется нулем, а остальные элементы получаются как результат вычитания соответствующего элемента матрицы выигрыша из максимального в своем столбце. Таким образом, в данном случае получаем:
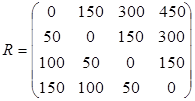
Теперь применяем формулу (13):
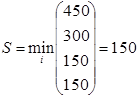
Причем минимум дают сразу две стратегии - А3 и А4, которые и являются наилучшими с точки зрения критерия Сэвиджа.
Критерий пессимизма-оптимизма Гурвица. Согласно этому критерию, оптимальной считается стратегия, для которой выполняется соотношения:
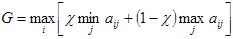 , (14)
, (14)
где 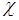 – коэффициент пессимизма-оптимизма, который принимает значения в диапазоне
– коэффициент пессимизма-оптимизма, который принимает значения в диапазоне
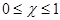 . Случай
. Случай 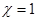 соответствует критерию Вальда, т.е. крайнему пессимизму. При
соответствует критерию Вальда, т.е. крайнему пессимизму. При 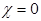 возникает ситуация крайнего оптимизма, когда в матрице выигрышей отыскивается самый большой элемент. Обычно принимают
возникает ситуация крайнего оптимизма, когда в матрице выигрышей отыскивается самый большой элемент. Обычно принимают 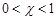 , и конкретное значение коэффициента задается из субъективных соображений. Здесь в условиях задачи указано
, и конкретное значение коэффициента задается из субъективных соображений. Здесь в условиях задачи указано 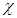 = 0,6. Применим формулу (14):
= 0,6. Применим формулу (14):
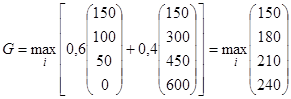 =240
=240
Согласно критерию Гурвица, оптимальной следует считать стратегию А4. Как видим, эта стратегия появляется в качестве оптимальной второй раз.
Критерий максимума математического ожидания выигрыша. Поскольку вероятности состояний природы нам неизвестны, принимаем все состояния равновероятными, т.е. 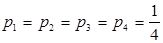 .
.
Отсюда средний выигрыш от применения i –й стратегии:
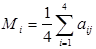 (15)
(15)
Среди этих средних выигрышей выбираем максимальный:
М1 = ¼ ( 150 + 150 + 150 + 150) = 150;
М2 = ¼ ( 100 + 300 + 300 + 300) = 250;
М3 = ¼ ( 50 + 250 + 450 + 450 ) = 300;
М4 = ¼ ( 0 + 200 + 400 + 600 ) = 300.
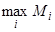 = М3 = М4 = 300. Имеем две оптимальные стратегии - А3 и А4.
= М3 = М4 = 300. Имеем две оптимальные стратегии - А3 и А4.
Критерий минимального среднего риска. Аналогичен предыдущему критерию, однако анализу подвергается матрица рисков:
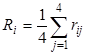 (16)
(16)
Из этих средних значений рисков применения каждой стратегии выбираем наименьшее. Применим формулу (16), получим:
R1 = ¼ ( 0 + 150 + 300 + 450 ) = 225;
R2 = ¼ ( 50 + 0 + 150 + 300 ) = 125;
R3 = ¼ ( 100 + 50 + 0 + 150 ) = 75;
R4 = ¼ ( 150 + 100 + 50 + 0 ) = 75.
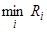 = R3 = R4 = 75. Здесь также имеем две оптимальные стратегии - А3 и А4.
= R3 = R4 = 75. Здесь также имеем две оптимальные стратегии - А3 и А4.
Таким образом, по совокупности критериев наилучшей следует принять стратегию А4. Это и есть решение задания.
Случай. Вероятности состояний природы известны (варианты 6 - 10).
Вновь рассмотрим приведенное выше задание, но с известными вероятностями состояний природы.
| Величины прибыли | ||||
| План продажи | Состояние спроса | |||
| П1 | П2 | П3 | П4 | |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 | ||||
| Pj | 0,3 | 0,2 | 0,4 | 0,1 |
Выполнение задания в этих вариантах имеет следующие особенности:
1) Применение критериев Вальда и Сэвиджа не отличается от вариантов 1-5.
2) В формуле (14) для критерия Гурвица принять 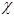 =0,5.
=0,5.
3) Формулы (15), (16) примут соответствующий вид:
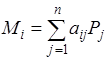 (или
(или 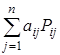 ) (17)
) (17)
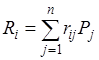 (или
(или 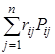 ) (18)
) (18)
Таким образом, для рассматриваемых условий имеем:
М1 = 150 × 0,3 + 150 × 0,2 + 150 × 0,4 + 150 × 0,1 = 150,
М2 = 100 × 0,3 + 300 × 0,2 + 300 × 0,4 + 300 × 0,1 = 240,
М3 = 50 × 0,3 + 250 × 0,2 + 450 × 0,4 + 450 × 0,1 = 290,
М4 = 0 × 0,3 + 200 × 0,2 + 400 × 0,4 + 600 × 0,1 = 260.
По критерию максимума математического ожидания выигрыша имеем 
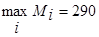 , что соответствует наилучшей стратегии А3.
, что соответствует наилучшей стратегии А3.
Для средних рисков имеем:
R1 = 0 × 0,3 + 150 × 0,2 + 300 × 0,4 + 450 × 0,1 = 195,
R2 = 50 × 0,3 + 0 × 0,2 + 150 × 0,4 + 300 × 0,1 = 105,
R3 = 100 × 0,3 + 50 × 0,2 + 0 × 0,4 + 150 × 0,1 = 55,
R4 = 150 × 0,3 + 100 × 0,2 + 50 × 0,4 + 0 × 0,1 = 85.
Отсюда 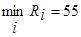 , что соответствует наилучшей стратегии А3.
, что соответствует наилучшей стратегии А3.
По совокупности критериев в данном случае оптимальной следует принять стратегию А3.
ВАРИАНТЫ ЗАДАНИЙ
ЗАДАЧА № 1.
| вариант | a1 | a2 | a3 | b1 | b2 | b3 | р1 | р2 | р3 | Dр1 | Dр2 | Dр3 | a | b |
| -100 | ||||||||||||||
| -130 | ||||||||||||||
| -90 | ||||||||||||||
| -65 | ||||||||||||||
| -50 | ||||||||||||||
| -92 |
ЗАДАЧА № 2.
1.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
2.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
3.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
4.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
5.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
6.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
7.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
8.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
9.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
10.
| Потребители | В1 | В2 | В3 | В4 | В5 | Запасы |
| Базы | (аi) | |||||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности (bj) |
Задача № 3
Варианты 1,2. Розничное торговое предприятие разработало несколько вариантов продажи товаров на предстоящей ярмарке с учетом меняющейся структуры рынка и спроса покупателей, получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров.
1. æ = 0,7
| Величина прибыли, тыс.руб. | ||||
| План | Состояние конъюнктуры рынка и спроса | |||
| продажи | К1 | К2 | К3 | К4 |
| П1 | 5,0 | 4,5 | 5,1 | 4,0 |
| П2 | 4,2 | 5,6 | 3,9 | 4,3 |
| П3 | 3,6 | 4,1 | 4,7 | 4,0 |
| П4 | 3,5 | 3,9 | 4,6 | 3,8 |
2. æ = 0,6
| Величина прибыли, тыс.руб. | ||||
| План | Состояние конъюнктуры рынка и спроса | |||
| продажи | К1 | К2 | К3 | К4 |
| П1 | ||||
| П2 | ||||
| П3 | ||||
| П4 |
Варианты 3-5. Экономисты оптового торгового предприятия на основе возможных вариантов поведения поставщиков П1, П2, П3, П4, (П5) разработали несколько своих хозяйственных планов О1, О2, О3, О4, а результаты всех возможных исходов представили в виде матрицы прибыли (выигрышей). Определить оптимальный план оптового торгового предприятия.
3. æ = 0,8
| Хозяйствен- | Прибыль по каждому варианту, тыс.руб. | |||
| ный план | П1 | П2 | П3 | П4 |
| О1 | 2,3 | 3,4 | 3,0 | 3,4 |
| О2 | 3,0 | 2,9 | 2,6 | 3,7 |
| О3 | 2,8 | 3,8 | 3,6 | 3,0 |
| О4 | 4,0 | 2,9 | 4,0 | 4,2 |
4. æ = 0,7
| Хозяйствен- | Прибыль по каждому варианту, тыс.руб. | |||
| ный план | П1 | П2 | П3 | П4 |
| О1 | ||||
| О2 | ||||
| О3 | ||||
| О4 |
5. æ = 0,6
| Хозяйствен- | Прибыль по каждому варианту, тыс.руб. | ||||
| ный план | П1 | П2 | П3 | П4 | П5 |
| О1 | 0,8 | 1,4 | 3,2 | 2,6 | 2,2 |
| О2 | 4,2 | 0,1 | 1,6 | 2,2 | 3,4 |
| О3 | 2,6 | 3,8 | 0,2 | 0,4 | 3,2 |
| О4 | 1,4 | 4,0 | 2,0 | 5,2 | 0,6 |
Варианты 6,7. Розничное предприятие торговли формирует заявку на новые товары Н1, Н2, Н3, заменяющие старые товары, хорошо известные покупателям. Методы изучения спроса позволили составить матрицу условных вероятностей (Рij) продажи старых товаров С1, С2, С3 при наличии конкурирующих новых товаров в торговой сети.
Составить план-заказ на товары, чтобы обеспечить оптимальное соотношение между их продажей.
6.
| Старые | Новые товары | ||
| товары | Н1 | Н2 | Н3 |
| С1 | 9 0,6 | 6 0,3 | 4 0,1 |
| С2 | 8 0,2 | 3 0,7 | 7 0,1 |
| С3 | 5 0,1 | 5 0,4 | 8 0,5 |
7.
| Старые | Новые товары | ||
| товары | Н1 | Н2 | Н3 |
| С1 | 6 0,7 | 7 0,1 | 5 0,2 |
| С2 | 7 0,6 | 5 0,2 | 8 0,2 |
| С3 | 5 0,6 | 3 0,3 | 6 0,1 |
Варианты 8-10.Предприятие общественного питания планирует выпуск трех партий новых, ранее не производимых полуфабрикатов П1, П2, П3, в условиях неясной рыночной конъюнктуры, относительно которой известны лишь отдельные возможные состояния Р1, Р2, Р3, Р4, а также возможные объемы товарооборота по каждому варианту, и их условные вероятности, которые представлены в виде (Рij) матрицы. Определить предпочтительный план выпуска полуфабрикатов.
8.
| Партии полу-фабрикатов | Объем товарооборота при различных состояниях рыночной конъюнктуры | |||
| Р1 | Р2 | Р3 | Р4 | |
| П1 | 2,2 0,4 | 3,8 0,1 | 2,8 0,2 | 3,2 0,3 |
| П2 | 2,6 0,3 | 2,4 0,2 | 3,1 0,1 | 3,3 0,4 |
| П3 | 3,0 0,2 | 2,0 0,3 | 1,8 0,2 | 2,5 0,3 |
9.
| Партии полу-фабрикатов | Объем товарооборота при различных состояниях рыночной конъюнктуры | |||
| Р1 | Р2 | Р3 | Р4 | |
| П1 | 2,4 0,2 | 0,9 0,3 | 1,7 0,2 | 1,2 0,3 |
| П2 | 1,4 0,3 | 1,8 0,2 | 1,3 0,1 | 1,6 0,4 |
| П3 | 1,2 0,4 | 2,0 0,1 | 1,8 0,2 | 1,3 0,3 |
10.
| Партии полу-фабрикатов | Объем товарооборота при различных состояниях рыночной конъюнктуры | |||
| Р1 | Р2 | Р3 | Р4 | |
| П1 | 1,2 0,3 | 2,1 0,2 | 1,7 0,1 | 2,0 0,4 |
| П2 | 1,5 0,4 | 1,3 0,1 | 1,6 0,2 | 1,8 0,3 |
| П3 | 1,7 0,2 | 1,6 0,3 | 1,9 0,2 | 1,4 0,3 |
