Краткие теоретические сведения. Корреляция представляет собой меру зависимости переменных
Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от –1,00 до +1,00. Значение –1,00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1,00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0,00 означает отсутствие корреляции.
Корреляция Пирсона предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале. Она определяет степень, с которой значения двух переменных «пропорциональны» друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и массой будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость можно представить прямой линией (с положительным или отрицательным углом наклона).
Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.
Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации (r2) представляет долю вариации, общую для двух переменных (иными словами, степень зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как величину корреляции, так и ее значимость.
Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т. е. отклонений наблюдений от регрессионной прямой) для зависимой переменной Y является нормальным (с постоянной дисперсией для всех значений независимой переменной X).
Несколько слов о выбросах. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.
Обычно считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. К сожалению, не существует общепринятого метода автоматического удаления выбросов. Чтобы не быть введенными в заблуждение полученными значениями, необходимо проверить на диаграмме рассеяния каждый важный случай значимой корреляции. Очевидно, выбросы могут не только искусственно увеличить значение коэффициента корреляции, но также реально уменьшить существующую корреляцию.
Если после выполнения процедуры поиска и удаления выбросов коэффициент корреляции остался низким и уровень значимости меньше критического 0,05, то следует увеличить размер выборки, воспользовавшись простым соотношением:  .
.
Корреляционный анализ
Выполнение корреляционного анализа покажем на примере результатов измерения массы (Y) и длины туловища (X) подопытных животных. Исходные данные представлены в таблице 6.1
(в табличном редакторе MS Excel данные представлены двумя столбцами).
Шаг 1. Откройте модуль Анализ данных,выберитеопцию Корреляция, после чего щелкните мышкой OK.
Шаг 2. В появившемся окне выполните операции и установки, как показано на рисунке 6.1.
Шаг 3. Щелкнете мышкой OK. Результат обработки появится в указанном поле (выходной интервал $Е$1, таблица 6.2).
Таблица 6.1 – Исходные данные
| X | Y | X | Y | X | Y |
| 3,4 | 14,3 | 8,4 | 19,8 | 10,7 | 21,3 |
| 3,6 | 14,9 | 8,5 | 19,9 | 11,6 | 21,3 |
| 4,5 | 17,3 | 8,8 | 19,9 | 21,8 | |
| 4,8 | 17,3 | 8,9 | 20,1 | 12,3 | |
| 4,9 | 17,4 | 8,9 | 20,1 | 12,6 | 22,1 |
| 5,2 | 17,5 | 8,9 | 20,1 | 12,7 | 22,4 |
| 5,4 | 17,6 | 8,9 | 20,1 | 13,3 | 22,7 |
| 5,7 | 17,6 | 20,2 | 13,6 | 23,5 | |
| 6,2 | 17,6 | 20,3 | 13,8 | 24,2 | |
| 6,7 | 17,8 | 9,1 | 20,3 | 24,4 | |
| 7,1 | 9,3 | 20,5 | 25,2 | ||
| 7,5 | 9,4 | 20,6 | 15,2 | 25,2 | |
| 7,7 | 18,1 | 9,7 | 20,9 | 15,8 | 25,3 |
| 7,8 | 18,1 | 9,7 | 15,9 | 25,7 | |
| 7,9 | 18,6 | 9,9 | 21,1 | 16,6 | 26,8 |
| 19,7 | 10,1 | 21,1 | 17,1 | 27,5 |
Рисунок 6.1 – Стартовая панель
Таблица 6.2 – Результат обработки
| X | Y | |
| X | 0,98 | |
| Y | 0,98 |
Регрессионный анализ
Для выполнения регрессионного анализа использовались исходные данные таблицы 6.1.
Шаг 1. Откройте модуль Анализ данныхи выберитеопцию Регрессия, после чего щелкните мышкой OK.
Шаг 2. В появившемся окне выполните операции и установки, как показано на рисунке 6.2.
Шаг 3. Щелкните мышкой OK. Результат обработки появится в указанном поле (выходной интервал $L$1, рисунок 6.2,
таблицы 6.3–6.5).
Рисунок 6.2 – Стартовая панель
Таблица 6.3 – Результат обработки
| Параметры | Значения |
| Множественный R | 0,98 |
| R-квадрат | 0,97 |
| Нормированный R-квадрат | 0,97 |
| Стандартная ошибка | 0,53 |
| Наблюдения |
Таблица 6.4 – Дисперсионный анализ
| Параметры | df | SS | MS | F | Значимость F |
| Регрессия | 397,27 | 397,27 | 1403,61 | 0,000.. | |
| Остаток | 13,586 | 0,28 | |||
| Итого | 410,86 |
Таблица 6.5 – Регрессионный анализ
| Параметры | Коэффициенты | Стандартная ошибка | t-статистика | P-значение |
| Y-пересечение | 12,67 | 0,224 | 56,628 | 0,000.. |
| X | 0,82 | 0,0218 | 37,465 | 0,000.. |
Таким образом, корреляционная связь между массой и длиной туловища подопытных животных характеризуется высоким (r = 0,98) и достоверным коэффициентом корреляции (из таблицы 6.4: критерий Фишера F = 1403,61 при уровне значимости существенно
меньше 0,05). Получена очень надежная регрессия, о чем свидетельствует t-статистика из таблицы 6.5 (уровень значимости существенно меньше 0,05).
Уравнение линейной регрессии Пирсона и коэффициент корреляции: 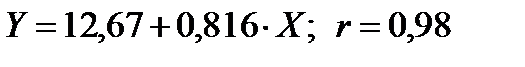 .
.
С менее подробной информацией операции регрессии и корреляции можно выполнить в системе MS Excel, используя модуль Мастер диаграмм.
Шаг 1. В системе MS Excel откройте модуль Мастер диаграмм (рисунок 6.3).
Рисунок 6.3 – Стартовая панель
Шаг 2. Выберите Тип диаграммыТочечная.
Шаг 3. Щелкните по кнопке Далее. Выберите диапазон данных (рисунок 6.4), оформите график и нажмите Готово.
Рисунок 6.4 – Диапазон данных
Шаг 4. На графике щелкните правой кнопкой по любой точке диаграммы.
Шаг 5. Выберите опцию Добавить линию трендаи Тип – линейная(рисунок 6.5). Щелкните мышкой OK.
Рисунок 6.5 – Тип аппроксимации кривой
Шаг 6. В опции Параметры выберите установки, как показано на рисунке 6.6. Щелкните мышкой OK.
Отредактированная диаграмма представлена на рисунке 6.7.
Рисунок 6.6 – Параметры кривой
Рисунок 6.7 – Отредактированная диаграмма
Уравнение регрессии и коэффициент детерминации R2 находятся в правом нижнем углу диаграммы. Как видно, что они такие же, как и при выполнении регрессионного анализа в пакете Анализ данных Регрессия.
Задания для выполнения
1 Введите в таблицу MS Excel исходные данные из Приложения Б (таблица Б1).
2 Отредактируйте и проверьте их на наличие артефактов в табличном редакторе MS Excel.
3 Выполните подготовительные и расчетные процедуры в соответствии с порядком операций, выполненных в настоящем разделе.
4 Получите результат и сделайте заключение.
Лабораторная работа 7
Парная корреляция (Statistica 6)
Цель работы: научиться выполнять корреляционный и регрессионный анализ, используя программный продукт Statistica 6.
