Распределительный метод решения транспортных задач.

1. Достаточные условия оптимальности. Допустим, что для некоторой транспортной задачи построен базисный план перевозок 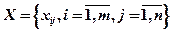с множеством базисных клеток U_б и небазисных клеток U_н. Выясним условия, при выполнении которых этот базисный план будет оптимальным. Для этого рассмотрим произвольную небазисную клетку 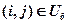и цикл, который она образует с базисными клетками. Допустим, что это цикл простейшей прямоугольной формы:

		k		j
i		cik -- xij	…	cij +
		…	…	…
l		clk + xkj	…	cl j -- xlj

Увеличим объем перевозок от i-го поставщика к j-ому потребителю на 1 (поскольку (i,j)-ая клетка пуста, то мы просто делаем объем поставки x_ij=1). Так как X – план транспортной задачи, то для него выполняются ее ограничения: 1) сумма поставок в каждой строке равна запасам поставщика ( ); 2)сумма поставок в каждом столбце равна потребностям потребителя ( 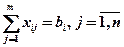). Поэтому простое увеличение объема поставок в одной отдельно взятой клетке невозможно – оно приведет к нарушению ограничений.

Чтобы разрешить эту проблему, используем клетки цикла. Раз объем поставки в клетке (i,j) увеличился на 1, уменьшим на эту же величину объем поставки в клетке (l,j). Благодаря этому суммарный объем поставок в j-ом столбце останется неизменным и соответствующее ему ограничение не нарушится. Зато нарушится баланс в l-ой строке – сумма поставок уменьшится на единицу. Поэтому увеличим на 1 объем поставки от l-ого поставщика к k-му потребителю. Это изменение, в свою очередь, повлечет за собой уменьшение на 1 поставки в клетке (i,k) – и цикл замкнулся, все изменения взаимно компенсировали друг друга. Такое свойство характерно для любого цикла в транспортной таблице.

Поскольку план перевозок изменился, то в общем случае изменились и транспортные затраты. Подсчитаем величину этого изменения, обозначив его через Δ_ij.Объем перевозок в клетке (i,j) увеличился на единицу, следовательно затраты, связанные с этой клеткой возросли на c_ij денежных единиц. В клетке (l,j) объем перевозок снизился на 1, а поэтому транспортные затраты уменьшились на c_lj денежных единицу. И т.д. В клетках транспортной таблицы, не вошедших в цикл, объемы поставок не изменились, а поэтому они не участвуют в формировании величины Δ_ij. Следовательно,

Δ_ij=с_ij-c_lj+c_lk-c_ik. (1)

Обобщим формулу (1) на случай произвольного цикла. Обойдем клетки цикла, начиная с клетки (i,j), в определенном направлении, например, по часовой стрелке, и пометим их по очереди знаками «+» и «-» (начнем с клетки (i,j), которую пометим знаком «+»). Введем следующие обозначения: 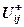- множество клеток цикла, помеченных знаком «+», - множество клеток цикла, помеченных знаком «-». Тогда

. (2)

Величина Δ_ij играет очень важную роль в исследовании транспортных задач и имеет простую экономическую интерпретацию: она показывает, как реагирует целевая функция задачи на единичное изменение объема поставки в небазисной клетке. Если Δ_ij>0, то с увеличением x_ij транспортные затраты увеличиваются, с уменьшением - уменьшаются; если Δ_ij<0, то при увеличении x_ij транспортные затраты снижаются, при уменьшении - уменьшаются; при Δ_ij=0, то целевая функция не чувствительна к изменению x_ij. Поэтому ее называют оценкой небазисной клетки.

По предположению X – базисный план перевозок. Так как (i,j)- небазисная клетка, то x_ij=0.Это означает, что в небазисной клетке возможно только увеличение объема поставок. Поэтому транспортные затраты можно уменьшить только в том случае, если среди оценок небазисных клеток есть хотя бы одна отрицательная. Если все оценки неотрицательны, то добиться уменьшения целевой функции невозможно. Последнее означает оптимальность базисного плана транспортной задачи. Таким образом, справедливо* следующее утверждение:

Теорема (достаточное условие оптимальности базисного плана): если

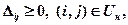(2)

то базисный план перевозок оптимален.

Применим достаточное условие оптимальности для анализа базисного плана перевозок, построенного в предыдущем параграфе методом северо-западного угла. Для этого вычислим оценки всех небазисных клеток.

Потр Пост 9 Δ12=с12-с11+с21-с22=1-9+5-1=-4<0	Потр Пост 30 Δ13=с13-с11+с21-с23=1-9+5-2=-5<0
Потр Пост 30 Δ14=с14-с11+с21-с23+с33-с34= 7-9+5-2+1-5=-3<0	Потр Пост 2 Δ24=с24-с23+с33-с34=6-2+1-5=0
Потр Пост 5 Δ31=с31-с21+с23-с33=4-5+2-1=0>0	Потр Пост 50 Δ32=с32-с22+с23-с33=2-1+2-1=0>0

Три первых оценки являются отрицательными и не удовлетворяют достаточному условию оптимальности (2). Следовательно, представленный в таблице план, является неоптимальным и его можно улучшить.

2. Вычисление максимально допустимой циркуляции. Из рассуждений, проведенных в предыдущем пункте, видно, что изменение объема поставки в любой небазисной клетке на величину Θ=1 приводит к циклическому изменению на величину ± Θ всех объемов поставок в базисных клетках, с которыми образует (единственный!) цикл небазисная клетка. При этом понятно, что величина Θ может принимать любые допустимые в задаче значения, а не только 1. Ниже величину Θ, на которую циклически изменяются объемы поставок в транспортной задаче, будем называть циркуляцией (Θ=1 – единичная циркуляция).

Предположим, что базисный план транспортной таблицы не удовлетворяет условиям оптимальности (2). По аналогии с симплекс-методом выберем из отрицательных оценок максимальную по модулю. Допустим, что она находится в клетке (i_*,j_*). Эту клетку в дальнейшем будем называть ведущей.

Построим цикл 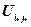, который образует клетка (i_*,j_*) с базисными клетками таблицы, и разметим его знаками «+» и «-». Изменим объем поставки от i_* -го поставщика к j_*-му потребителю на величину циркуляции Θ>0и рассмотрим изменения, произошедшие в клетках цикла 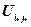, обозначив через 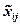измененные объемы поставок:

(3)

Формулы (3) отражают простой факт: циркуляция добавляется в клетках, помеченных знаком «+», и вычитается в клетках, помеченных знаком «-».

Уменьшение транспортных затрат прямо пропорционально циркуляции Θ и составляет величину 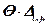, т.е. чем больше циркуляция, тем меньше затраты. Однако циркуляция не может быть скол угодно большой, поскольку объемы поставок не могут быть отрицательными. Действительно, в клетках цикла, помеченных знаком «-», объемы поставок уменьшаются на величину циркуляции. При больших Θ все они могут стать отрицательными. Чтобы этого не произошло, рассчитаем максимально допустимую циркуляцию.

Так как отрицательные объемы могут появиться только в клетках, помеченных знаком «-», то в силу (3) максимально допустимая циркуляция не может быть больше минимального объема поставки в этих клетках. Обозначим максимально допустимую циркуляцию через Θ⁰. Тогда

. (4)

Таким образом, для вычисления максимально допустимой циркуляции необходимо найти минимальное из чисел x_ij, находящихся в клетках цикла, помеченных знаком «-».

Применим проведенные рассуждения к рассматриваемому примеру. Максимальную по модулю отрицательную оценку имеет клетка (1,3). Построим и разметим для этой клетки цикл:

Потр Пост
	9 --		1 +
30
	5 +		2 --

Согласно (4)

Θ⁰=min{30,0}=0

В данном случае проявилась специфика рассматриваемого примера: базисный план вырожден, т.е. содержит фиктивно заполненную клетку. Именно эта клетка вошла в цикл и оказалась помеченной знаком «-». Поэтому максимально допустимая циркуляция оказалась равной 0. Следует отметить, что подобная ситуация на практике встречается достаточно редко.

Построение нового базисного плана. Допустим, что в результате расчета максимально допустимой циркуляции оказалось, что

.

Здесь 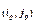- координаты клетки, которая «обусловила» величину максимально допустимой циркуляции. По аналогии с симплекс-методом будем называть эту клетку разрешающей.

Построение нового базисного плана перевозок включает

1) пересчет плана перевозок. Понятно, что изменения коснутся только тех клеток транспортной таблицы, которые составили вместе с ведущей клеткой цикл 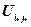: в клетках цикла, помеченных знаком «+», объемы перевозок нужно увеличить на величину ; в клетках цикла, помеченных знаком «-», объемы перевозок нужно уменьшить на величину . Формально это правило записывается так:

2) преобразование базиса. Так же как и в симлекс-методе, разрешающая клетка покидает базис, вместо нее вводится ведущая:

Применение этих правил к нашему примеру означает, что план перевозок фактически не изменится ( ). Клетка (2,3) выводится из базиса (освобождаем ее от фиктивного нуля), клетка (1,3) – вводится в базис (ее заполняем фиктивным нулем):

Потр Пост

Дальнейшее решение проводится по описанной выше схеме..

* Строго говоря, проведенные рассуждения не являются точным математическим доказательством. Они, скорее, иллюстрируют, объясняют утверждение, сформулированное в качестве теоремы.