Построение сокращенной ДНФ методом Блейка.

Минимизация булевых функций.

Совершенные нормальные формы записи логических функций дают однозначное представление логических функций, но иногда являются очень громоздкими. Поэтому для булевых функций, представленных в виде СДНФ или СКНФ, возникает задача минимизации.

Индексом простоты (или сложностью) булевой функции называется функция 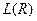, определенная на множестве всех ДНФ и удовлетворяющая следующим свойствам:

1) Свойство неотрицательности: ;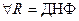

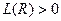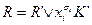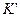2) Свойство монотонности: если , где -элементарная конъюнкция, .

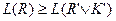3) Свойство выпуклости: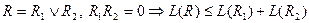

4) Свойство инвариантности: если ДНФ = 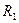получена из ДНФ = 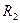путем переименования переменных без отождествления, то .

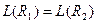Примеры. 1) 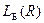- число букв переменных, встречающихся в записи 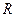. Под буквой понимают символ переменной или ее отрицание, если переменная 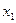входит в формулу m раз, то говорят, что формула содержит m букв 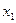. Например в выражении 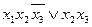число переменных равно 3, а число букв равно 5, т.е. число букв равно числу вхождений переменных.

2) 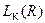- число элементарных конъюнкций, входящих в .

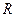3) 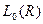- число символов отрицаний, встречающихся в записи 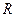. Каждый из указанных индексов удовлетворяет перечисленным свойствам.

Пример. Пусть 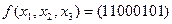задана вектором состояний. Тогда для нее может быть записана СДНФ в виде

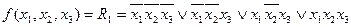
Эту функцию можно упростить

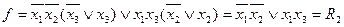
Вычислим индексы простоты для 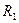и .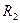

, ; , ;

, .

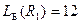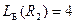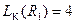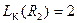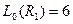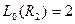Следовательно, 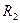проще 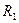для всех трех индексов простоты.

Задача минимизации заданной логической функции сводится к представлению ее дизъюнктивной (или конъюнктивной) нормальной формой, имеющей наименьший индекс простоты. В качестве индекса простоты наиболее часто используется индекс .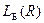

Пример.

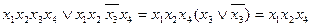
Построение сокращенной ДНФ методом Блейка.

Сокращенной д.н.ф.функции 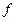называется функция, которая содержит меньшее число букв, чем СДНФ. Если над СДНФ произвести все возможные операции склеивания, а затем все возможные операции поглощения то полученная функция будет иметь вид сокращенной ДНФ.

В основе использования метода Блейка лежат операции склеивания и операции поглощения.

Законы поглощения

,

,

,

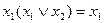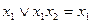
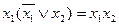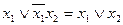
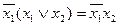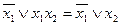
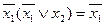
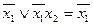
Отметим, что формулы во втором столбце получаются из формул первого столбца с помощью принципа двойственности.

Закон склеивания (объединения конъюнкций): .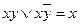

Закон обобщенного склеивания: .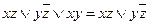

Пример. Получить сокращенную ДНФ методом Блейка

1) .

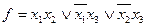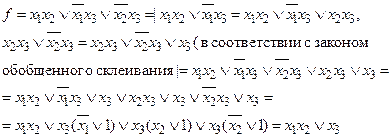
Минимизация булевых функций методом Квайна– Мак-Класки.

Импликантой 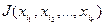функции 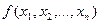называется конъюнкция некоторых аргументов из набора 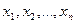и их отрицаний, обладающая следующими свойствами:

1) Если на некотором наборе 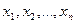импликанта 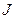принимает значение 1, то и 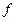принимает на этом наборе значение 1.

2 При исключении хотя бы одного множителя из 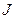свойство 1) не выполняется.

Пример.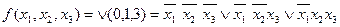

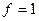на наборах (0,0,0), (0,0,1), (0,1,1).

Рассмотрим 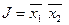. 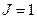на наборах (0,0,0), (0,0,1). На этих наборах 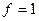, т.е. выполняется условие 1).

Если вычеркнуть один множитель из 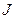и оставить, например, 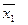, то. 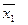принимает значение 1 на наборах (0 0 0), (0 0 1), (0 1 0), (0 11), причем на выделенном наборе 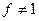. Аналогичным образом , 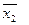принимает значение 1, причем на выделенных наборах 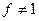. Следовательно, при вычеркивании одного множителя у 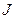свойство 1) не выполняется. Это означает, что 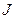является импликантой функции.

Пусть на некотором наборе 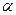функция 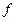обращается в 1. Если на этом наборе импликанта 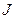функции обращается в 1, то говорят, что импликанта 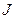накрывает эту единицу функции .

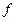Система импликант функции 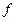называется полной, если любая единица из таблицы значений функции 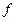накрывается хотя бы одной импликантой.

Сокращенной ДНФ функции 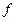называется дизъюнкция всех импликант из полной системы импликант.

Утверждение. Сокращенная ДНФ. функции 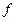совпадает с самой функцией.

Действительно, дизъюнкция всех импликант из полной системы импликант равна 1 на тех наборах, где равна 1 функция ( в соответствии с определением импликанты 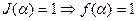) и равна нулю на тех наборах, где равна нулю функция, т.е. значения сокращенной д.н.ф.функции 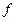и функции 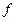совпадают.

Сокращенная д.н.ф.функции 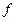содержит меньшее число букв, чем СДНФ Однако, во многих случаях допускается дальнейшее сокращение числа букв за счет того, что некоторые из импликант могут поглощаться дизъюнкциями других импликант.