Уравнение Михаэлиса-Ментен

Главной целью изучения кинетики ферментативных реакций является получение информации, которая может способствовать выяснению молекулярного механизма действия фермента.

Общие принципы кинетики химических реакций применимы и к ферментативным реакциям. Известно, что любая химическая реакция характеризуется константой термодинамического равновесия. Она выражает состояние химического равновесия, достигаемого системой, и обозначается К_р. Так, для реакции

k+1 , k-1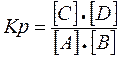

константа равновесия равна произведению концентраций образующихся веществ, деленному на произведение концентрации исходных веществ. Значение константы равновесия обычно находят из соотношения констант скоростей прямой (k₊₁) и обратной (k-₁) реакций, т.е. К_p = k₊₁/k-₁. В состоянии равновесия скорость прямой реакции: v₊₁ = k₊₁[А]·[B] равна скорости обратной реакции: v₁ = k_-1 [С]·[D], т. е. v₊₁ = v_-1 соответственно k₊₁[А]·[B] = k_-1[С]·[D], или

.

Отсюда,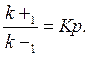

Таким образом, константа равновесия равна отношению констант скоростей прямой и обратной реакций. Величину, обратную константе равновесия, принято называть в случае ферментативной реакции константой диссоциации фермент–субстратного комплекса, и обозначать символом K_S. Так, в реакции

k+1 k-1

,

т.е. K_S равна отношению произведения концентрации фермента и субстрата к концентрации фермент-субстратного комплекса или отношению констант скоростей обратной и прямой реакций. Следует отметить, что константа K_S зависит от химической природы субстрата и фермента и определяет степень их сродства. Чем ниже значение K_S, тем выше сродство фермента к субстрату.

При изучении кинетики ферментативных реакций следует учитывать одну важную особенность этих реакций, не свойственную обычным химическим реакциям и связанную с явлением насыщения фермента субстратом. При низкой концентрации субстрата зависимость скорости реакции от концентрации субстрата (рис. 14.19) ляется почти линейной и подчиняется кинетике первого порядка.

Рис. 14.19. График зависимости скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента: а – реакция первого порядка; б – реакция смешанного порядка; в – реакция нулевого порядка

Это означает, что скорость реакции S→Р прямо пропорциональна концентрации субстрата S и в любой момент времени t определяется следующим кинетическим уравнением:

,

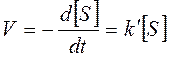где [S] – молярная концентрация субстрата; –d[S]/dt – скорость убыли субстрата; k' – константа скорости реакции, которая в данном случае имеет размерность, обратную единице времени (мин^–1 или с^–1).

При высокой концентрации субстрата скорость реакции максимальна, постоянна и не зависит от концентрации субстрата. В этом случае реакция подчиняется кинетике нулевого порядка v = k′′ (при полном насыщении фермента субстратом) и целиком определяется концентрацией фермента. Кроме того, различают реакции второго порядка, скорость которых пропорциональна произведению концентраций двух реагирующих веществ. В определенных условиях при нарушении пропорциональности иногда говорят о реакциях смешанного порядка (см. рис. 14.19).

Изучая явление насыщения, Л. Михаэлис и М. Ментен разработали общую теорию ферментативной кинетики. Они исходили из предположения о том, что ферментативный процесс протекает в виде следующей химической реакции:

k+1 k+2 , k-1

т.е. фермент Е вступает во взаимодействие с субстратом S с образованием промежуточного комплекса ES, который далее распадается на свободный фермент и продукт реакции Р. Принимая во внимание, что скорость ферментативной реакции определяется константой каталитического превращения фермент-субстратного комплекса (k₊₂) и его концетрации, Михаэлис и Ментен предложили уравнение, выражающее количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции:

где v – наблюдаемая скорость реакции при данной концентрации субстрата; K_S– константа диссоциации фермент-субстратного комплекса, моль/л; V_max– максимальная скорость реакции при полном насыщении фермента субстратом.

Из уравнения Михаэлиса–Ментен следует, что при высокой концентрации субстрата и низком значении K_S скорость реакции является максимальной, т.е. v = V_max (реакция нулевого порядка, см. рис. 14.19). При низкой концентрации субстрата, скорость реакции напротив, оказывается прямопропорциональной концентрации субстрата в каждый данный момент (реакция первого порядка).

Следует указать, что уравнение Михаэлиса-Ментен в его классическом виде не учитывает влияние на скорость ферментативного процесса продуктов реакции и носит несколько ограниченный характер.

k+1 k+2 k-1 k-2

В связи с этим были предприняты попытки усовершенствовать уравнение, что было сделано Бриггсом и Холдейном:

,

где К_m - константа Михаэлиса, являющаяся экспериментально определяемой величиной. Она может быть представлена следующим уравнением:

, или .

В числителе – константы скоростей распада комплекса ES в двух направлениях (в сторону исходных Е и S и в сторону конечных продуктов реакции Е и Р). Отношение k_–1/ k₊₁ представляет собой константу диссоциации фермент-субстратного комплекса K_S. Тогда

Отсюда вытекает важное следствие: константа Михаэлиса всегда больше константы диссоциации фермент-субстратного комплекса K_S на величину k₊₂/k₊₁.

Для определения численного значения К_m обычно находят ту концентрацию субстрата, при которой скорость ферментативной реакции v составляет половину от максимальной V_max, т.е. если v = ¹/₂ V_maх. Подставив значение v в уравнение Бриггса–Холдейна, получаем:

.

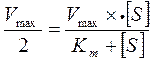Разделив обе части уравнения на V_mах, получим:

,

откуда Km = [S]

Таким образом, константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость данной ферментативной реакции составляет половину от максимальной.

Определение величины К_m имеет важное значение при выяснении механизма действия эффекторов на активность ферментов и т.д. Константу Михаэлиса можно вычислить по графику (рис. 14.20).

Рис. 14.20. Гиперболическая зависимость начальной скорости катализируемой ферментом реакции от концентрации субстрата (график уравнения Михаэлиса-Ментен)

Отрезок на абсциссе, соответствующий скорости, равной половине максимальной, будет представлять собой К_m.

Единицы ферментов

Определение количественного содержания ферментов в биологических объектах представляет известные трудности поскольку, за редким исключением ферменты в тканях присутствуют в ничтожно малых концентрациях. Поэтому о количестве ферментов судят по скорости катализируемой реакции в определенных, согласованных условиях измерения. При оптимальных условиях температуры, рН среды и полном насыщении фермента субстратом скорость катализируемой реакции пропорциональна концентрации фермента. О скорости ферментативной реакции судят или по скорости убыли субстрата, или по скорости образования продукта реакции. Для выражения концентрации фермента и количественной оценки его активности в условных единицах Комиссией по ферментам Международного биохимического союза была рекомендована стандартная международная единица (Е или U): за единицу активности любого фермента принимается то его количество, которое в оптимальных условиях катализирует превращение одного микромоля субстрата или образование одного микромоля продукта в минуту (мкмоль/мин). Единицы активности фермента выражают также в наномолях (10^-9моль) и пикомолях (10^-12 моль).

В связи с введением Международной системы единиц (СИ) предложено новое выражение активности фермента в каталах (кат, kat): 1 кат есть каталитическая активность, способная осуществлять реакцию со скоростью, равной 1 молю в 1 с (1 моль/с). Отношение международной единицы (U) к каталу можно выразить следующим образом: 1 кат = 1 моль·с^-1 = 60 моль·мин^-l = 60·10⁶ мкмоль·мин^-l = 6·10⁷U, или 1 U = 1 мкмоль·мин^-l = 1/60) мкмоль·с^-l = 1/60) мккат = 16,67 нкат. Таким образом, 1 U фермента соответствует 16,67 нкат.

Кроме того, рекомендовано измерять активность фермента при температуре 25°С, оптимуме рН и концентрации субстрата, превышающей концентрацию насыщения. В этих случаях скорость соответствует нулевому порядку реакции в отношении субстрата и зависит только от концентрации фермента.

В практике для выражения активности часто пользуются произвольными понятиями удельной и молярной активности. Удельную активность фермента принято выражать числом единиц ферментативной активности на 1 мг белка (или числом каталов на 1 кг активного белка). Количество молекул субстрата, подвергающихся превращению одной молекулой фермента в продукт в процессе реакции в единицу времени при полном насыщении фермента субстратом, принято называть числом оборотов фермента, или молярной активностью (молярная каталитическая активность выражается в каталах на 1 г/моль фермента). Так, одна молекула каталазы эритроцитов способна, например, расщепить в одну секунду 44000 молекул перекиси водорода. В то же время для того, чтобы 1 атом неорганического железа, также катализирующий распад H₂O₂, расщепил такое число молекул H₂O₂, которое расщепляет каталаза в одну секунду, потребовалось бы несколько лет. Этот пример является наглядным доказательством одного из главных свойств ферментов – их высокой каталитической активности.

ЛЕКЦИЯ 15