Типовые задачи детерминированного факторного анализа
В детерминированном факторном анализе можно выделить четыре типовые задачи:
1. Оценка влияния относительного изменения факторов на относительное изменение результативного показателя.
2. Оценка влияния абсолютного изменения i-го фактора на абсолютное изменение результативного показателя.
3. Определение отношения величины изменения результативного показателя, вызванного изменением i-го фактора, к базовой величине результативного показателя.
4. Определение доли абсолютного изменения результативного показателя, вызванного изменением i-го фактора, в общем изменении результативного показателя.
Охарактеризуем эти задачи и рассмотрим решение каждой из них на конкретном простом примере.
Пример.
Объем валовой продукции (ВП) зависит от двух основных факторов первого уровня: численности работников (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: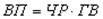 
. Рассмотрим ситуацию, когда и выработка, и численность рабочих в отчетном периоде отклонились от запланированных значений.
Данные для расчетов приведены в таблице 1.
Таблица 1. Данные для факторного анализа объема валовой продукции.
| Показатель | Условное обозначение | План | Факт | Отклонение |
| Валовая продукция, млн. руб. | ВП | 160 000 | 240 000 | 80 000 |
| Среднегодовая численность рабочих, чел. | ЧР | +200 | ||
| Среднегодовая выработка одного рабочего, млн. руб. | ГВ | +40 |
Задача 1.
Задача имеет смысл для мультипликативных и кратных моделей. Рассмотрим простейшую двухфакторную модель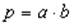 
. Очевидно, что при анализе динамики этих показателей будет выполняться следующее соотношение между индексами:
,
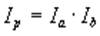где значение индекса находится отношением значения показателя в отчетном периоде к базисному.
Рассчитаем индексы валовой продукции, численности работников и среднегодовой выработки для нашего примера:
;
.
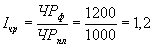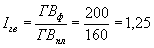Согласно вышеприведенному правилу, индекс валовой продукции равен произведению индексов численности работников и среднегодовой выработки, т. е.
.
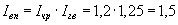Очевидно, что если мы рассчитаем непосредственно индекс валовой продукции, то получим то же самое значение:
.
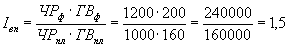Мы можем сделать вывод: в результате увеличения численности работников в 1,2 раза и увеличения среднегодовой выработки в 1,25 раза объем валовой продукции увеличился в 1,5 раза.
Таким образом, относительные изменения факторных и результативного показателей связаны той же зависимостью, что и показатели в исходной модели. Данная задача решается при ответе на вопросы типа: "Что будет, если i-й показатель изменится на n%, а j-й показатель изменится на k%?".
Задача 2.
Является основной задачей детерминированного факторного анализа; ее общая постановка имеет вид:
Пусть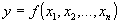 
- жестко детерминированная модель, характеризующая изменение результативного показателя y от n факторов; все показатели получили приращение 
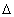(например, в динамике, по сравнению с планом, по сравнению с эталоном):
; 
.
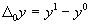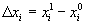Требуется определить, какой частью приращение результативного показателя y обязано приращению i-го фактора, т. е. расписать следующую зависимость:
,
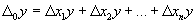где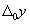 
- общее изменение результативного показателя, складывающееся под одновременным влиянием всех факторных признаков;
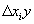- изменение результативного показателя под влиянием только фактора 
.
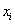В зависимости от того, какой метод анализа модели выбран, факторные разложения могут различаться. Поэтому рассмотрим в контексте данной задачи основные методы анализа факторных моделей.