Приведение процентной ставки к базовому периоду

Общепринято процентную ставку указывать за базовый период, равный одному году, а процентную ставку rTза фактический период Т вычислять по схеме простых или сложных процентов. При использовании схемы простых процентов составляется обычная пропорция

r – TБ

rT – T

где rТ – процентная ставка за период Т; r – процентная ставка за базовый период ТБ.

Откуда процентная ставка за период Т будет равна

rT = r × T / TБ = r × t,

где t – срок в годах.

Если длительность краткосрочного вложения измеряется в днях, то длительность базового периода ТБ измеряется также в днях, но используют либо точную длительность (365 или 366 дней), либо, более часто, приближенную (360 дней или 12 месяцев, имеющих условно равную длительность в 30 дней).

При расчетах процентных ставок за период, охватывающий несколько полных лет, используют схему сложных процентов

(1 + rT)= (1 + r)T.

Отсюда процентная ставка за период Т будет рассчитываться по формуле

rT = (1 + r)T – 1.

Если известна денежная сумма в начальный и конечный моменты времени, то подставляя в последнюю формулу вместо (1 + rT) отношение FV/ PV и разрешая полученное уравнение относительно r, получим формулу для расчета годовой процентной ставки по формуле сложных процентов

r = (FV / PV)1/T– 1.

С помощью процентной ставки может быть определена как будущая стоимость «сегодняшних» денег (например, если их собираются ссудить), так и настоящая (современная, текущая или приведенная) стоимость «завтрашних» денег – например, тех, которыми обещают расплатиться через год после поставки товаров или оказания услуг. В первом случае говорят об операции наращения, поэтому будущую стоимость денег часто называют наращенной. Во втором случае выполняется дисконтирование или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приведенная или текущая стоимость.

Будущая стоимость денег

Будущая стоимость денег представляет собой сумму инвестированных в настоящий момент средств, в которую они превратятся через определенный период времени с учетом определенной процентной ставки. Определение будущей стоимости денег характеризует процесс наращения их стоимости (компаундинг), который состоит в присоединении к их первоначальной сумме начисленной суммы процентов.

Наращенной суммой называется результат сложения первоначальной денежной суммы и начисленных процентов, а наращением – процесс вычисления наращенной суммы.

Метод наращения используется для вычисления денежной суммы, которая будет получена через определенное время, если на первоначальную сумму будут начисляться проценты по действующей процентной ставке.

FV = PV∙(1 + r),

где FV – будущая стоимость денег; PV – настоящая стоимость денег; r – процентная ставка (десятичная дробь).

Поскольку процентная ставка задается, как правило, в годовом исчислении, то используя формулу приведения к базовому периоду, получаем

FV = PV∙(1 + r · t / 365),

где r – годовая процентная ставка (десятичная дробь); t– срок в днях.

Если срок задается в годах, то формула расчета будущей стоимости денег имеет вид:

FV = PV∙(1 + r · t),

где r – годовая процентная ставка (десятичная дробь); t– срок в годах.

По методу начисления проценты можно разделить на простые и сложные. Критерием их разделения выступает база начисления. При простых процентах база начисления остается неизменной на всем протяжении срока начисления, то есть проценты начисляются на ту сумму капитала, которая была в начальный момент времени:

FV = PV∙(1 + r·n),

где r – процентная ставка за период начисления процентов (десятичная дробь); n – число периодов начисления процентов.

Начисление простого процента применяется, как правило, при краткосрочных финансовых операциях.

В случае начисления сложных процентов база начисления изменяется во времени и возрастает каждый раз, когда к основной сумме долга добавляются проценты, начисленные в предыдущем периоде. Такой процесс называется капитализацией процентов. В результате темп прироста конечной суммы при начислении по сложной ставке процентов оказывается значительно выше, чем при простой ставке. Формула расчета будущей стоимости денег по формуле сложных процентов имеет вид

FV = PV∙(1 + r)n,

где r – процентная ставка за период начисления процентов (десятичная дробь); n – число периодов начисления процентов.

Если период начисления процентов задается в годах, то формула наращения имеет вид:

FV = PV∙(1 + r)t,

где r – годовая процентная ставка (десятичная дробь); t– период в годах.

При начислении процентов несколько раз в году будущая стоимость денег рассчитывается по формуле:

FV = PV∙(1 + r / m)m·n,

где r – номинальная годовая процентная ставка (десятичная дробь); m – периодичность начисления процентов в году;n – количество лет начисления процентов.

В зависимости от количества выплат в год (m) внутригодовое начисление процентов может быть:

- полугодовым (m = 2);

- поквартальным (m = 4);

- ежемесячным (m = 12);

- ежедневным (m = 365);

- непрерывным (m -> ∞).

Начисление сложного процента применяется, как правило, при долгосрочных финансовых операциях (инвестировании, кредитовании и т.п.).

При начислении процентов нецелое число лет принято применять смешанный метод начисления, при котором сложные проценты начисляются на целое число периодов, а начисление дробной части ведется по простой ставке процента:

FV = PV∙(1 + r)n∙(1 + r∙k),

где r – процентная ставка за период начисления процентов (десятичная дробь); n – число периодов начисления процентов; k – дробная часть периода начисления процентов.

Эффективная процентная ставка при начислении процентов несколько раз в году измеряет тот реальный относительный доход, который будет получен за год. Иначе говоря, она отвечает на вопрос, какую годовую ставку сложных процентов нужно установить, чтобы получить такой же финансовый результат, как и при m-разовом начислении процентов в году по ставке r / m.

Из равенства наращенных сумм следует

(1 + rэ)n= (1 + r / m)m·n,

откуда эффективная процентнаяrэ рассчитывается по формуле

rэ = (1 + r / m)m– 1.

Настоящая стоимость денег

Настоящая стоимость денег представляет собой сумму будущих денежных средств, приведенной с учетом определенной ставки процента к настоящему периоду времени. Определение настоящей стоимости денег характеризует процесс дисконтирования их стоимости, который представляет операцию, обратную наращению, осуществляемую путем изъятия из будущей стоимости соответствующей суммы процентов (дисконтной суммы или «дисконта»).

Настоящей стоимостью денег называется текущая стоимость будущей денежной выплаты (серии выплат) с поправкой на определенную процентную ставку, а дисконтированием процесс вычисления настоящей стоимости, или процесс, обратный начислению процентов. Метод дисконтирования по своей сути противоположен методу наращения и используется для определения суммы, которую необходимо уплатить сейчас при заданном уровне процентной ставки, для того чтобы получить доход в будущем.

Формула дисконтирования по простой ставке следует из формулы наращения и имеет следующий вид:

PV = FV / (1 + r·t/365),

где PV – приведенная стоимость; FV – будущая стоимость; r – годовая процентная ставка (десятичная дробь); t – срок инвестиции.

Полученная сумма PV является приведенной стоимостью будущей суммы FV, которая образуется через tдней при действующей процентной ставке r.

Формула дисконтирования по ставке сложных процентов с начислением процентов за период

PV = FV / (1 + r)n,

где r – процентная ставка за период начисления процентов (десятичная дробь); n – число периодов начисления процентов.

Формула дисконтирования по ставке сложных процентов с начислением процентов m раз в году

PV = FV / (1 + r / m)n·m,

Банковское дисконтирование основано на использовании учетной ставки d, то есть проценты начисляются на сумму, подлежащую уплате в конце периода инвестиции.

При банковском дисконтировании по простой учетной ставке приведенная стоимость определяется по формуле

PV = FV·(1 – d·t),

где d – годовая учетная ставка (десятичная дробь); t – период дисконтирования в годах.

PV = FV·(1 – d · t / 365),

где d – годовая учетная ставка (десятичная дробь); t – период дисконтирования в днях.

Дисконтирование по сложной учетной ставке

PV = FV·(1 – d)n,

где d – учетная ставка за период дисконтирования; n – число периодов дисконтирования.

Формула дисконтирования по сложной учетной ставке с дисконтированием процентов несколько раз в году

PV = FV·(1 – d / m)n·m,

где d – годовая учетная ставка; m – число периодов дисконтирования в течение года;n – число лет.

Учет инфляции

В финансовом менеджменте постоянно приходится считаться с фактором инфляции, которая с течением времени обесценивает стоимость находящихся в обращении денежных средств.

Концепция учета фактора инфляции в управлении различными аспектами финансовой деятельности предприятия заключается в необходимости реального отражения стоимости его активов и денежных потоков, а также в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами.

Инфляция характеризуется такими показателями, как уровень (темп) и индекс инфляции.

Темп (уровень) инфляции (i) показывает, на сколько процентов повысились цены за определенный период времени:

i =ΔP / P · 100%,

где ΔP - прирост цен на товары потребительской корзины в отчетном периоде; Р - цены на товары, учитываемые при оценке инфляционного фактора (той же корзины) в базовом периоде.

Индекс инфляции показывает, во сколько раз повысились цены за рассматриваемый период:

I = (P+ΔP) / P · 100%.

Взаимосвязь темпа и индекса инфляции за один и тот же период времени такова:

I =i + 1.

Для определения индекса инфляции за длительный период (например, за один год) на основании значений уровня инфляции за более короткие периоды (например, месяцы), используют формулу

I = (1 +i1)(1 + i2) … (1 + in),

где n - количество периодов.

При равных периодах и равных уровнях инфляции за каждый период формула примет вид:

I = (1 +i)n.

В расчетах, связанных с корректировкой стоимости денег с учетом фактора инфляции принято использовать два понятия - номинальная и реальная сумма денежных средств.

Номинальная сумма денежных средств отражает оценку размеров денежных активов в соответствующих денежных единицах без учета изменения покупательной стоимости денег в рассматриваемом периоде.

Реальная сумма денежных средств отражает оценку размеров денежных активов с учетом изменения уровня покупательной стоимости денег в рассматриваемом периоде, вызванного инфляцией.

Для расчета этих сумм при наращении или дисконтировании стоимости денег во времени используют соответственно номинальную и реальную ставка процента.

Номинальная процентная ставка характеризует ставку процента, устанавливаемую без учета изменения покупательной способности денег в связи с инфляцией (или общую процентную ставку, в которой не исключена ее инфляционная составляющая).

Реальная процентная ставка характеризует ставку процента, устанавливаемую с учетом изменения покупательной стоимости денег в рассматриваемом периоде в связи с инфляцией.

Связь между номинальной (r) и реальной (rP) процентными ставками описывается формулой Фишера (названа именем американского ученого И. Фишера, который ее предложил):

rP = (r –i) / (r +i).

С учетом фактора инфляции будущая стоимость денежных средств (FV) рассчитывается по формуле

FV =PV·[(1 + r)·(1+i)]n,

где PV – настоящая стоимость денежных средств; r – реальная процентная ставка (десятичная дробь); i – уровень инфляции (десятичная дробь);n – количество периодов, по которым осуществляются процентные платежи.

С учетом фактора инфляции настоящая стоимость денежных средств (PV) рассчитывается по формуле

PV =FV / [(1 +r)·(1 + i)]n,

где FV – будущая стоимость денежных средств; r – реальная процентная ставка (десятичная дробь); i – уровень инфляции (десятичная дробь); n – количество периодов, по которым осуществляются процентные платежи.

Денежный поток

Денежный поток представляет собой совокупность ряда распределенных во времени поступлений и выплат денежных средств. Денежные потоки генерируются хозяйственной деятельностью предприятия, от реализации инвестиционного проекта или использования какого-либо актива, отдельными финансовыми операциями и инструментами и т.д.

Структурно денежный поток состоит из следующих элементов:

- притока или поступления денежных средств;

- оттока или выплат денежных средств.

1. По частоте платежей или количеству поступлений денежных средств различают:

- разовые потоки;

- срочные (конечные)потоки;

- бессрочные (бесконечные)потоки.

Разовый поток состоит из одной выплаты и последующего поступления либо разового поступления и последующей выплатой. Под срочным (конечным) потоком понимается поток с денежными поступлениями в течение ограниченного времени. Под бессрочным (бесконечным) потоком понимается поток с денежными поступлениями в течение длительного или неограниченного времени.

2. По величине интервалов между поступлениями денежных средств различают:

- денежные потоки с равными (постоянными) интервалами;

- денежные потоки с неравными (непостоянными) интервалами.

Денежный поток с равными интервалами между поступлениями называются рентой.

3. По равенству отдельных платежей различают:

- денежные потоки с равными поступлениями;

- денежные потоки с неравными поступлениями.

Денежный поток с равными интервалами и равными поступлениями (рента с равными поступлениями) называется аннуитетом.

4. По моменту поступления денежных средств в выбранном временном интервале различают потоки с поступлениями денежных средств:

- в начале интервала;

- в конце интервала;

- в любой момент интервала.

Денежный поток с поступлениями в начале периода называется потоком пренумерандо, с поступлениями в конце периода – постнумерандо.

Количественный анализ денежных потоков, генерируемых хозяйственной операцией за определенный период времени, в общем случае сводится к вычислению следующих основных характеристик:

FV – будущая стоимость денежного потока за n периодов;

PV – современная стоимость денежного потока за n периодов.

В дальнейшем при рассмотрении методов определения выделенных характеристик будем предполагать, что все денежные выплаты/поступления и начисление процентов осуществляются в конце соответствующего периода.

Денежный поток в виде платежей и выплат произвольной величины в произвольные моменты времени представляет собой наиболее распространенный случай хозяйственных операций. Типичными операциями, в результате которых возникают произвольные денежные потоки, являются вложения в долгосрочные активы производственного назначения, выплаты дивидендов по обыкновенным акциям и др.

Будущая стоимость денежного потока (FV) с произвольными величинами выплат или поступлений в любой момент времени рассчитывается по формуле:

где CFt – промежуточная выплата или поступление в момент времени t; r – годовая процентная ставка (десятичная дробь); t – срок до промежуточной выплаты или поступления; n – общее число промежуточных выплат и поступлений.

Настоящая (приведенная) стоимость денежного потока (PV) с произвольными величинами выплат или поступлений в любой момент времени рассчитывается по формуле:

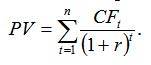
Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют аннуитетом (annuity). В финансовой практике часто встречаются так называемые простые, или обыкновенные, аннуитеты, которые предполагают получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце каждого периода (года, полугодия, квартала, месяца и т. д.). Выплаты по купонным облигациям, банковским кредитам, долгосрочной аренде, страховым полисам, формирование различных фондов – все это примеры обыкновенных аннуитетов.

Согласно определению простой аннуитет обладает двумя важными свойствами.

1. Все n элементов аннуитета равны между собой: CF1 = CF2 ...= CFn = CF;

2. Отрезки времени между выплатой/получением сумм CF одинаковы, то есть tn – tn-1, = ... = t2 – t1.

Будущая стоимость простого аннуитета представляет собой сумму всех составляющих его платежей с начисленными процентами на конец срока проведения операции:

Настоящая стоимость простого аннуитета представляет собой сумму всех составляющих его платежей, дисконтированных на момент начала операции:

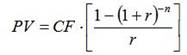
Выражение в квадратных скобках представляет собой множитель, равный современной стоимости аннуитета в 1 денежную единицу. Разделив настоящую стоимость PV денежного потока любого вида на этот множитель, можно получить величину периодического платежа CF эквивалентного ему аннуитета.

где CF – периодический платеж по аннуитету, эквивалентному произвольному денежному потоку по величине настоящей стоимости PV.

Эта математическая зависимость часто используется в финансовом и инвестиционном анализе для приведения потоков с неравномерными поступлениями к виду обыкновенного аннуитета.

Приведенная стоимость бессрочного аннуитета (при n -> ∞)

РV = C / r.

Риск и его оценка

Риск относится к возможности наступления какого-либо неблагоприятного события. Финансовый риск связан с неопределенностью эффективности операции в момент заключения сделки, обусловленной невозможностью точного определения цены или доходности в будущем. Поэтому финансовая операция считается рискованной, если ее эффективность не полностью известна в момент заключения сделки.

Риск предполагает вероятность потерь от непредвиденных убытков, недополучения ожидаемых доходов. В условиях рынка риск выступает как обратная сторона конкуренции, результат колебаний спроса и предложения на рынке капитала и товаров, изменений экономической ситуации в стране, регионе и на самом предприятии. В связи с этим успешное управление хозяйственной и финансовой деятельностью невозможно без учета риска.

Существуют различные виды рисков. Так, по видам деятельности риски можно подразделить на производственный, коммерческий и финансовый.

Производственный риск появляется в результате нарушения сроков поставок сырья, материалов, из-за неритмичности технологического и производственных процессов, роста издержек производства и других непредвиденных потерь.

Коммерческий риск присутствует в сфере обращения, сопутствует торговым сделкам, реализации товаров и услуг. Причиной его возникновения становятся существенные изменения рыночной конъюнктуры, колебания цен, неритмичность поставок продукции, изменение установленного ассортимента, увеличение потерь при транспортировке товаров и т.д.

Финансовый риск сопровождает всю сложную сферу финансовых взаимоотношений. Его причиной становятся имения в режиме кредитования, страхования, налогообложения, платежеспособности отдельных предприятии и других действий, связанных с финансовыми операциями и платежами.

Риски в зависимости от сферы управления подразделяются на хозяйственный, рыночный и инвестиционный.

Хозяйственный риск рассматривается как широкое понятие которое включает вероятность недополучения ожидаемых положительных конечных результатов. Его уровень выражается в снижении объема производимой и реализованной продукции, уменьшении денежных поступлений, превышении величины планируемых затрат и снижения прибыли.

Рыночный риск является постоянной величиной всех трансакций, возникает как следствие стихии рынка, конкуренции, соответствующих изменений между спросом и предложением. Он выражается в колебаниях цен, неплатежеспособности отдельных субъектов, резком изменении рыночной стоимости разных товарно-материальных ценностей и имущества предприятий. Учет последствии рыночного риска возможен при постоянном анализе конъюнктуры рынка, ее реальной оценке и обосновании прогнозов изменений на основе сложившейся главной тенденции и намечаемых на перспективу мероприятий, общей экономической ситуации в стране и регионе.

Инвестиционный риск вызван непредвиденными изменениями эффективности текущих вложений при реализации осуществляемого проекта. Его величина бывает особенно высокой, поскольку зависит от многих параметров. Ухудшение общей экономической ситуации в стране, на фондовом и денежных рынках, изменения в финансовом законодательстве могут значительно увеличить степень инвестиционного риска.

Инвестиционный риск включает в себя общие хозяйственный и рыночные риски, а также риск финансовой ликвидности и платежеспособности. Риск ликвидности определяется, прежде всего, появлением серьезных препятствий в реализации отдельных видов активов хозяйствующего субъекта. Риск платежеспособности особенно заметен в длительном инвестиционном процессе при невыполнении финансовых обязательств, увеличении задолженности по ссудам и другим взаимным расчетам.

Субъекты хозяйствования должны определять величину и возможные последствия всех видов рисков, формы их проявления, овладевать прогрессивными методами предвидения и способами снижения этого финансового инструмента.

Поскольку определенный риск неизбежен, то, прежде всего, необходимо установить его допустимый уровень, не угрожающий функционированию данного предприятия, а также принять меры, направленные на его предупреждение. Прогнозирование степени допустимого риска осуществляется различными методами.

Чаще всего для измерения риска используется среднеквадратичное отклонение

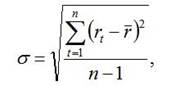
где rt – процентная ставка за период времени t; r - среднегодовая процентная ставка за n периодов, вычисляемая по формуле:

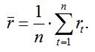
С точки зрения теории вероятностей среднеквадратичное отклонение служит мерой разброса значений случайной величины вокруг среднего значения. Поэтому для доходности ценной бумаги как случайной величины среднеквадратичное отклонение, оценивающее степень отклонения возможных конкретных значений доходности от средней или ожидаемой доходности, служит мерой риска, связанного с данной доходностью.

Таким образом, среднеквадратичное отклонение учитывает не только размер отклонений возможных значений доходности от среднего, но и вероятность такого отклонения. В этом смысле среднеквадратичное отклонение указывает меру неопределенности в ожиданиях инвестора, который оценивает будущую доходность как среднюю по всем возможным значениям. Это обстоятельство и позволяет считать среднеквадратичное отклонение мерой риска.

Помимо среднеквадратичного отклонения, для измерения степени риска можно использовать также коэффициент вариации, который представляет собой среднеквадратичное отклонение, деленное на ожидаемую доходность. Если доходность примерно одинаковая, то нет необходимости использовать коэффициент вариации, так как ценная бумага с большим стандартным отклонением будет иметь и более высокий коэффициент вариации. Если же доходность существенно отличается, то удобнее использовать коэффициент вариации, который будет показывать степень риска на единицу доходности. Поскольку доходность измеряется в процентах годовых, то коэффициент вариации будет показывать степень риска на 1 % годовых доходности. Коэффициент вариации вычисляется по формуле:

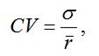
где CV – коэффициент вариации; σ – среднеквадратичное отклонение; r - ожидаемая доходность