Оценка риска инвестиционного портфеля
Принимая решение о целесообразности инвестирования денежных средств в финансовые активы, инвестор должен прежде всего оценить риск, присущий этим активам, затем - ожидаемую их доходность и далее определить, достаточна ли эта доходность для компенсации ожидаемого риска. Чаще всего инвестор работает не с отдельным активом, а с некоторым их набором, называемым портфелем ценных бумаг, или инвестиционным портфелем. Отсюда с очевидностью вытекает, что оценивая риск конкретного актива из инвестиционного портфеля, можно действовать двояко: либо рассматривать этот актив изолированно от других активов, либо считать его неотъемлемой частью портфеля. Оказывается, что оценка рисковости актива и целесообразности операции с ним при этом могут меняться. Более того, актив, имеющий высокий уровень риска при рассмотрении его изолированно, может оказаться практически безрисковым с позиции портфеля и при определенном сочетании входящих в этот портфель активов. Например, теоретически можно подобрать два финансовых актива, каждый из которых имеет высокий уровень риска, но которые, будучи объединенными вместе, составят абсолютно безрисковый портфель. Кроме того, увеличение числа включаемых в портфель активов, как правило, приводит к снижению риска данного портфеля. При оценке портфеля и целесообразности операций с входящими в него активами необходимо оперировать показателями доходности и риска портфеля в целом. Доходность портфеля (kp) представляет собой линейную функцию показателей доходности входящих в него активов и может быть рассчитана по формуле средней арифметической взвешенной (в данном случае речь может идти как об ожидаемой, так и о фактической доходности):

где kj - доходность j-го актива; dj - доля j-го актива в портфеле; n - число активов в портфеле.
Как и в случае с отдельными активами, мерой риска портфеля служит вариация его доходности.
В частности, если в качестве меры риска выбрано среднее квадратическое отклонение, то его значение для портфеля, содержащего k активов, может быть найдено по формуле:
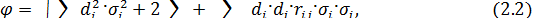
где di – доля i-го актива в портфеле; σi – вариация доходности i-го актива; Rij- коэффициент корреляции между ожидаемыми доходностями i-го и j-го активов.
Для портфеля из двух активов эта формула существенно упрощается и имеет вид:
φ = 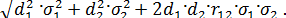 (2.3)
(2.3)
Безусловно, если инвестор владеет портфелем ценных бумаг, он будет заинтересован, прежде всего, в средней доходности портфеля в целом, однако задача оценки изолированного актива также имеет определенный интерес, в частности, для предельного случая, когда портфель инвестора состоит из одной ценной бумаги (имеется ввиду что инвестор владеет, например, n акциями одного эмитента).
