Расчет будущей стоимости проектов

Таблица 6

Годы	Проект А Чистый доход	Проект А Стоимость через 5 лет	Коэффициент сложных процентов r = 10%	Проект Б Чистый доход	Проект Б Стоимость через 5 лет
		219.62	(1+0.1)4=1.464	-110	-161.05
		199.65	(1+0.1)3=1.331		93.07
		181.50	(1+0.1)2=1.210		193.60
		165.00	(1+0.1)1=1.100		418.00
		150.00	1.000		300.00
Всего		915.77	6.105		843.72

Проект А с учетом использования получаемых доходов через 5 лед принесет в сумме 915.00 тыс. руб., что больше аналогичной стоимости проекта Б, которая равна 843.72 тыс. руб. Проект А более выгоден.

Решим эту же задачу с помощью программы Mathcad. Введем на рабочий лист процентную ставку, число лет от 1 до 5, векторы доходов и инвестиций обоих проектов и формулу для вычисления сложных процентов в обратной перспективе. Подставим в эту формулу оба вектора и получим таблички вычисленных доходов по правилу сложных процентов по годам.

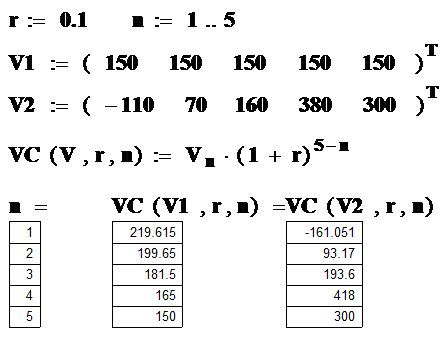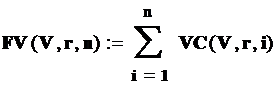Рассчитаем суммы доходов нарастающим итогом для обоих проектов по формуле

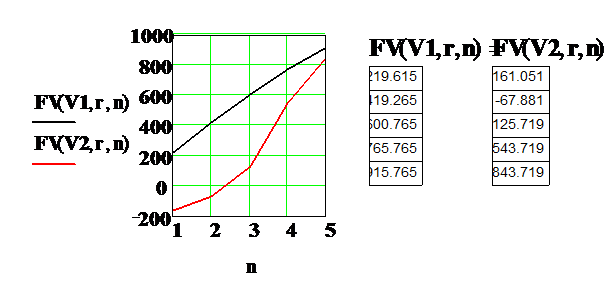
Приведем полученные результаты и построим графики для этих сумм.

Суммарный доход для каждого проекта можно вычислить с помощью финансовой функции fvc. Смысл аргументов и синтаксис функции понятен из приведенных формул. Наблюдаем полное совпадение результатов во всех трех вариантах вычислений.

МЕТОД ДИСКОНТИРОВАНИЯ

При оценке инвестиционного проекта в качестве альтернативной процентной ставки, то есть ставки, с которой сравнивают данный инвестиционный проект, принимается ставка банковского процента по депозитам или процент по государственным обязательствам плюс, как правило, надбавка за риск. Эта надбавка может учитывать как риски, связанные с самим проектом, так и риски, обусловленные, например, общей неблагоприятной экономической или политической обстановкой (значительной инфляцией, политической нестабильностью и т.п.).

Рассмотрим пример применения метода дисконтирования для оценки эффективности инвестиционного проекта. Пусть имеется начальный капитал 1000 тыс. руб. Инвестирование его в проект при сроке реализации 4 года дает ежегодный доход 300 тыс. руб. Рассчитаем чистую текущую стоимость доходов, используя коэффициенты дисконтирования (таблица 5).

РАСЧЕТ ЧИСТОЙ ТЕКУЩЕЙ СТОИМОСТИ ПРОЕКТА

Таблица 5

Годы	Доход	Коэффициенты дисконтирования	PV
при r1=10%	при r2=6%	10%	6%
	-	1.000	1.000	-	-
		0.9091	0.9434	272.37	283.02
		0.8264	0.8900	247.92	267.00
		0.7513	0.8396	225.40	251.88
		0.6830	0.7921	204.92	237.62
Всего		-	-	950.96	1039.48

Из таблицы следует, что при альтернативной процентной ставке 10% проект оказывается неэффективным, так как приведенная к настоящему времени сумма будущих доходов PV=950.96 тыс. руб. меньше требуемых инвестиций. Более выгодным проектом будет помещение капитала на депозит. Если же процентная ставка равна 6%, то приведение будущих доходов по проекту к настоящему времени дает PV=1039.48 тыс. руб., что несколько превышает инвестируемую сумму. Если не учитывать риски (инфляция и др.), то есть смысл инвестировать. Таким образом, оказывается, что выгодность или невыгодность одного и того же проекта зависит от внешних по отношению к проекту факторов.

Проанализируем предлагаемый инвестиционный проект с помощью программы Mathcad. Введем на рабочий лист объем инвестиций I, процентные ставки r1 и r2, число лет n от 1 до 4, величину ежегодного дохода P и формулу для вычисления ежегодного приведенного дохода PD(P,r,n) как функцию P, r и n. Подставим в эту формулу оба значения процентной ставки и получим таблички приведенных доходов по годам по

методу дисконтирования. Получим результаты, совпадающие с предыдущими вычислениями

Поставим задачу определения значений параметров задачи при которых проект становится выгодным. Для этого проекта изменим число лет n от 1 до 5 и вычислим сумму PV(P, r, n) приведенных доходов нарастающим итогом и вычислим эти суммы для обеих процентных ставок.

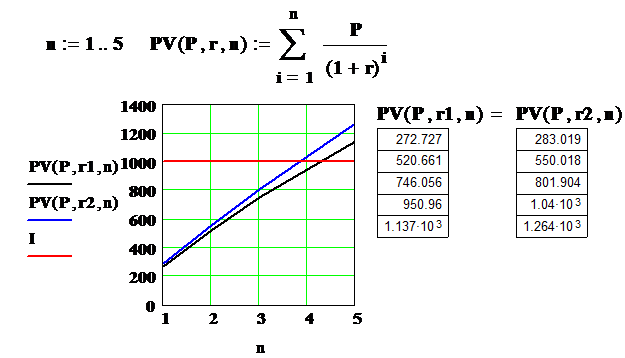
Из полученных данных, представленных в графической и табличной форме, следует, что при ставке r2 = 6% проект выгоден, а при ставке r1 = 10% сумма приведенных доходов меньше суммы инвестиций. При этой ставке приведенные доходы превысят инвестиции только за 5 лет.

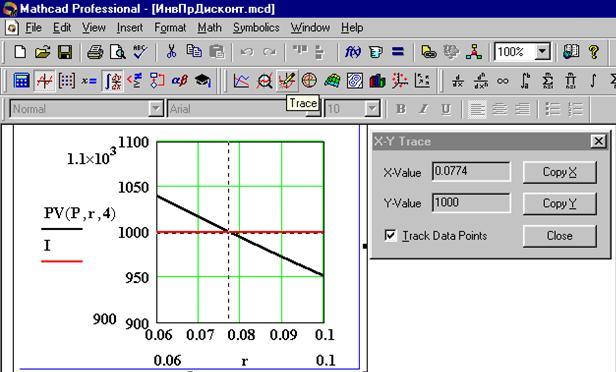
Определим графическим способом предельную процентную ставку, при которой инвестиции оправдают себя за 4 года. Для этого построим график PV(P, r, 4), как функции аргумента r. Подберем приемлемые интервалы изменения функции и масштабы графика по обеим осям. Затем воспользуемся дополнительной возможностью, имеющейся в программе Mathcad для графического анализа, – трассировкой графиков. Активизируем построенный график щелчком мыши и нажмем кнопку Trace в палитре Graph. На экране появится диалоговое окноX-Y Trace. Щелкнем снова на графике, после чего на нем появятся вертикальная и горизонтальная перекрещивающиеся пунктирные линии. Координаты пересечения этих линий отражены в окошках X-Value и Y-Value диалогового окнаX-Y Trace. Для того чтобы перекрестье автоматически отслеживало линию графика, поставим флажок в окошке Track Data Points. Переместим мышью перекрестье так, чтобы оно совпало с пересечением линий графика функции PV(P, r, 4) и горизонтальной линии I = 1000. Точность совпадения с последней контролируем по показанию окошка Y-Value (Y = 1000). В окошке читаем значение искомой предельной процентной ставки r = 0.0774 = 7.74%.

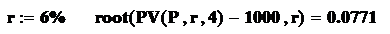Более точное значение предельной процентной ставки можно получить, решив уравнение PV(P, r, 4) – 1000 = 0 относительно неизвестной r с помощью функции root (корень).