Параметрическая модель рынка

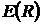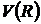Рассмотренная выше модель рынка основывалась на понятии пространства состояний рынка. Это идеализированное понятие, то есть состояние рынка – «ненаблюдаемая» величина. Однако значения доходностей активов являются величинами наблюдаемыми, то есть результаты наблюдений над доходностями за прошлые периоды позволяют получить статистические оценки для количественных оценок доходности – и или .

Это приводит к упрощенной модели рынка – параметрической или к модели рынка по Марковицу, описываемой тройкой:

, (6)

где - конечный набор активов рынка (портфеля), - вектор ожидаемых доходностей ( ), - ковариационная матрица.

Например, для № 1 параметрическая модель рынка имеет следующие компоненты

, ,

.

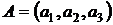Параметры такой модели статистически оцениваются соответствующими характеристиками. Так, если наблюдаемый временной ряд доходностей для последовательных периодов в прошлом имел вид: , то оценкой математического ожидания доходности является выборочное среднее:

;

дисперсия оценивается выборочной дисперсией:

;

стандартное отклонение – по корню квадратному из выборочной дисперсии:

.

Ковариация между активами и оценивается по выборочной ковариации:

,

и соответственно коэффициент корреляции оценивается по выборочному коэффициенту корреляции:

.

№ 4. Составить параметрическую модель рынка по результатам пяти наблюдений для пяти активов, приведенных в следующей таблице:

Таблица 3

Актив	Доходность за период (%)
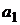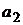				-2	-2

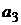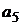Проанализировать характер зависимостей доходностей активов между собой, построив корреляционную матрицу.

Решение. Вычислим:

а) выборочные средние:

,

, , , ;

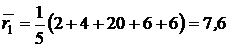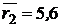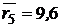б) выборочные коэффициенты ковариации:

, , ,

, , ,

, , ,

, , ,

, ;

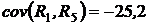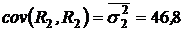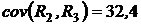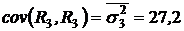в) выборочные парные коэффициенты корреляции:

,

,

, , ,

, , ,

, , .

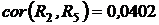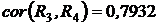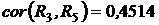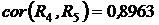Следовательно, ковариационная матрица примет вид:

,

а корреляционная матрица:

,

Анализ результатов построения корреляционной матрицы позволяет сделать следующие выводы:

1) Доходности активов №1, №4 и №1, №5 меняются в «разных направлениях».

2) Доходности остальных активов – в «одинаковых направлениях».

3) Наибольшая положительная корреляция наблюдается между активами №2, №3 и №4, №5.

4) Наибольшая отрицательная корреляция – между активами №1, №5.

5) Отсутствует значимая корреляционная зависимость между активами №2, №5 и №1, №4.

Рассмотренная выше вероятностная модель рынка 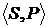является дискретной, так как число состояний рынка было выше принято считать конечным. Однако теоретически рынок может принимать бесконечное число состояний, то есть общая модель рынка должна включать в себя не только дискретный, но и непрерывный случай.

Тогда пространство состояний рынка, в общем виде, может быть записано как:

S ,

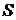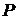где - множество состояний, - алгебра событий на S, - вероятностная мера на . И рынком будет называться тройка:

<S, A, R>,

где S - пространство состояний, 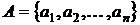- конечный класс активов, - конечное семейство случайных величин – доходностей активов за выбранный период времени .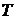

Из курса теории вероятностей известны следующие формулы для характеристик такого рынка:

,

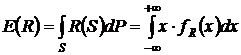где 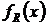- плотность распределения вероятностей случайной величины ,

,

и

.

Среди непрерывных случайных величин особо выделяется класс нормальных случайных величин, причем доходности активов считаются имеющими нормальное распределение.