Ожидаемая доходность и риск активов

Пусть имеется некоторый рынок активов (ценных бумаг)

,

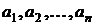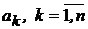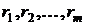где - отдельные активы. Каждому активу , поставим в соответствие случайную величину , которая представляет собой доходность данного актива в выбранном инвестиционном горизонте T. Эта величина в результате испытания (по истечении промежутка времени T) может принять следующие возможные значения (реализации)при соответствующих состояниях рынка . То есть 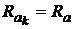, можно определить как дискретную случайную величину:

			…
			…

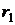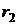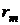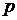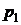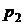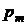где .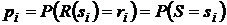

Тогда ожидаемая доходность актива a будет характеризоваться математическим ожиданием:

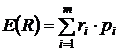, (1)

а мерой риска актива a является дисперсия (или вариация) случайной величины :

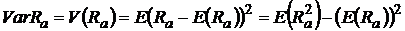, (2)

или

.

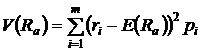Учитывая, что размерность дисперсии равна квадрату размерности доходности R, в качестве меры риска часто используют среднеквадратическое (или стандартное) отклонение:

.

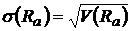Однако использование вариации в качестве меры риска не лишено недостатков. Дело в том, что вариация учитывает отклонения в обе стороны по отношению к среднему значению. То есть реализованная доходность может быть выше среднего значения, что вносит свой вклад в величину вариации, а следовательно и риска. Инвестор же не расценивает превышение реальной доходности над ожидаемой как неприятный результат. Напротив, он приветствует такой исход дела. Поэтому некоторые исследователи считают, что такие случаи не должны рассматриваться при измерении риска. Эту меру риска называют еще полувариацией. В настоящее время при измерении риска снижения стоимости ценной бумаги финансисты-практики пользуются обоими понятиями.

№ 1. Пусть рынок состоит из трех активов 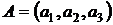и может находиться в одном из трех состояний , где 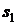- «хорошее» состояние (подъем), 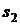- «среднее» состояние (равновесие) и 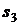- «плохое» состояние (спад). Данные по вероятностям и доходностям приведем в следующей таблице:

Таблица 1.

Состояние рынка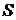	Вероятность	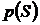Доходности активов (в %)
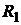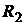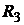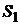	0,3			-10
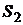	0,6
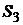	0,1		-20

Оцените доходности и риски данных активов.

Решение. Составим законы распределения случайных величин 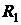, 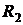и :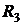

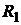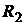							-20		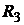	-10
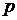	0,9	0,1		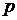	0,3	0,6	0,1			0,3	0,7

Тогда ожидаемые доходности равны:

,

,

.

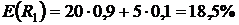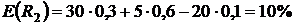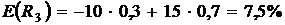Оценим риски этих активов:

, ;

, ;

, .

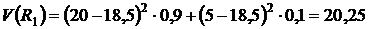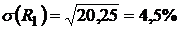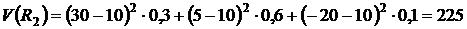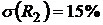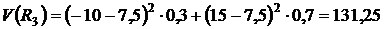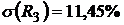Полученные результаты можно представить в виде следующей таблицы:

Таблица 2

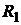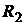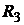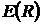	18,5		7,5
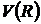	20,25		131,25
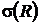	4,5		11,45

Из рассмотренного примера видно, что наибольшей доходностью 18,5% и наименьшим риском 4,5% обладает актив 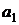, и если инвестор при принятии инвестиционных решений основывается лишь на рассмотренных выше характеристиках доходности и риска, то он должен инвестировать весь свой капитал в актив .

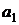Другими словами, если речь идет о выборе наилучшего актива, удовлетворяющего условиям:

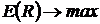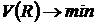, , (3)

то оптимальный портфель должен состоять только из актива 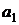.