Тема 5. Детерминированный факторный анализ.
Методика построения факторных моделей. Виды факторных моделей.
Приемы измерения влияния факторов в детерминированном факторном анализе.
После изучения темы 5. студент должен знать:
· виды связей между показателями;
· виды и методику построения детерминированных факторных моделей;
· приемы измерения влияния факторных показателей на результативный.
После изучения темы 5. студент должен уметь:
· построить структурно – логическую схему зависимости результативного показателя от факторных показателей;
· определить вид и тип детерминированной факторной модели;
· определить влияние факторов на результативный показатель.
Методика построения факторных моделей. Виды факторных
Моделей.
Количественное измерение влияния факторов в детерминированном анализе производится на основе факторной модели. Факторная модель представляет собой функциональную зависимость результативного показателя от факторных.
В анализе хозяйственной деятельности выделяются следующие виды моделей: аддитивная, мультипликативная, кратная и смешанная модели.
Аддитивная – это модель, в которой результативный показатель представляется в виде суммы факторных показателей.
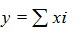 , (5.1)
, (5.1)
где:
y – результативный показатель;
хi – факторные показатели.
Примером аддитивной модели служат следующие зависимости.
(Прибыль отчетного года) = (прибыль по видам деятельности) + (сальдо операционных доходов и расходов) + (сальдо внереализационных операций).
(Капитал предприятия) = (капитал и резервы) + (обязательства)
Мультипликативная – это модель, в которой результативный показатель представлен в виде произведения факторных показателей.
( 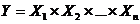 ), (5.2)
), (5.2)
где:
Y - результативный показатель;
X1, X2, X3, …, Xn.
Примером мультипликативной зависимости являются следующие модели.
(Выручка от реализации) = (количество реализованной продукции) х (цена)
(Среднегодовая выработка одного рабочего) = (среднечасовая выработка одного рабочего) х (среднечасовая продолжительность рабочего дня) х (среднее количество дней, отработанных, одним рабочим)
Кратной называется модель, в которой результативный показатель представлен в виде отношения факторных показателей.
 , (5.3)
, (5.3)
Примером кратной модели являются следующие.
(Издержкоемкость продукции) = (себестоимость продукции) / (стоимость продукции в ценах реализации без налогов и сборов, уплачиваемых из выручки)
(Фондоотдача основных средств)= (выработка одного рабочего) / (фондовооруженность)
Смешанной (комбинированной) моделью является модель, в которой результативный показатель представляется одновременно в виде суммы, отношения или произведения факторных показателей.
 , (5.4)
, (5.4)
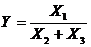 , (5.5)
, (5.5)
 , (5.6)
, (5.6)
Примером смешанной модели являются следующие.
(Рентабельность) =  , (5.7)
, (5.7)
где
МЗ - материальные затраты;
РОТ - расходы на оплату труда;
ОТЧ - отчисления на социальные нужды;
АМ – амортизация основных средств и нематериальных активов;
ПРЗ - прочие затраты.
Построить факторную модель – значит представить результативный показатель в виде алгебраической суммы, произведения или частного факторных показателей, оказывающих на результативный непосредственное влияние и находящихся с ним в функциональной связи.
Построение факторной модели включает следующие этапы:
1. Выделение структурно-логической модели и построение её в виде схемы. Установление факта детерминированной связи.
2. Запись исходной факторной модели с выделением факторов первого порядка.
Рассмотрим пример построения модели стоимости произведенной продукции от эффективности использования трудовых ресурсов.
(Стоимость произведенной продукции) = (среднесписочная численность рабочих) х (среднегодовая выработка одного рабочего)
ВП = Ч х W , (5.8)
где:
ВП - стоимость произведенной продукции;
Ч - среднесписочная численность рабочих;
W - среднегодовая выработка одного рабочего.
3. Представление факторной модели путём выделения факторов второго и третьего порядков
ВП = Ч х Тд х Wд, (5.9)
где:
Тд – среднее количество дней, отработанных одним рабочим;
Wд – среднедневная выработка одного рабочего.
ВП = Ч х Тд х Тч х Wч, (5.10)
где:
Тч – средняя продолжительность рабочего дня;
Wч – среднечасовая выработка одного рабочего.
4. Количественное змерение влияния факторов на результативный показатель.
5. Формулировка выводов по результатам проведенного факторного анализа о существенном (несущественном), положительном (негативном) влиянии факторов.
Требования к факторной функциональной модели:
ü Факторы должны носить реальный объективный характер
ü Факторные исследования должны носить познавательный характер и практическую ценность
ü Показатели должны иметь единицу измерения, количественное выражение
ü Модель должна обеспечивать равенство общего изменения результативного показателя и суммы его изменений под влиянием каждого фактора.
В теории анализа хозяйственной деятельности разработаны следующие приемы развития исходной факторной модели, которая имеет вид кратной:
1. Удлинение. Суть его состоит в представлении числителя в виде суммы новых факторов, при этом конечная факторная модель имеет вид смешанной или аддитивной
 , (5.11)
, (5.11)
Рассмотрим методику развития модели издержкоемкости продукции.
(Издержкоемкость продуции) = 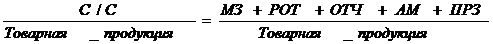 =
=
=МЕ + ЗплЕ + Уотч + АМЕ + Упрз, (5.12)
где: 
МЕ – материалоёмкость;
ЗплЕ – зарплатоёмкость;
Уотч - удельный вес отчислений на социальные нужды в стоимости продукции;
АМЕ - амортизациёмкость
Упрз - удельный вес прочих затрат в стоимости продукции.
2. Разложение. Состоит в представлении факторного показателя, стоящего в знаменателе, в виде суммы или произведения факторов.
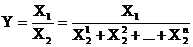 , (5.13)
, (5.13)
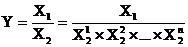 , (5.14)
, (5.14)
Рассмотри рентабельность оборота (рентабельность продаж, реализации).
Рпр= 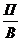 =
=  , (5.15)
, (5.15)
Рреал= 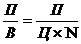 , (5.16)
, (5.16)
Где:
Рпр - рентабельность оборота;
Реал - рентабельность оборота;
Вi - выручка от реализации i- ого вида продукции;
Ц – цена продукции;
N – объем реализации продукции в натуральном выражении.
3.Расширение. Суть состоит в умножении числителя и знаменателя на одинаковые показатели.
 =
=  , (5.17)
, (5.17)

 , (5.18)
, (5.18)
где:
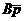 -среднегодовая выработка одного станка;
-среднегодовая выработка одного станка;
ВП - выпуск продукции;
 - среднее количество единиц оборудования;
- среднее количество единиц оборудования;
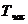 - отработано времени всем оборудованием;
- отработано времени всем оборудованием;
 - среднечасовая выработка
- среднечасовая выработка
 - среднее количество часов, отработанных единицей оборудования за год.
- среднее количество часов, отработанных единицей оборудования за год.
3. Сокращение. Суть состоит в делении числителя и знаменателя на одинаковые факторные показатели. Конечная факторная модель имеет вид кратной.
 , (5.19)
, (5.19)
Рассмотрим построение факторной модели рентабельности продукции. Рпрод= 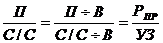 , (5.20)
, (5.20)
где:
Рпрод - рентабельность продукции;
С/С – себестоимость реализованной продукции;
П – прибыль от реализации продукции;
РПР – рентабельность оборота (продаж);
УЗ - уровень затрат на рубль выручки.
