Методы верификации прогнозных моделей

Метод верификации	Технология верификации
Прямая верификация	Разработка модели того же объекта с использованием иного метода прогнозирования
Косвенная верификация	Сопоставление результатов, полученных с использованием данной модели, с данными, полученными из других источников
Консеквентная верификация	Верификация результатов моделирования путем аналитического или логического выведения прогноза из ранее полученных прогнозов
Верификация оппонентом	Верификация путем опровержения критических замечаний оппонента по прогнозу
Верификация экспертом	Сравнение результатов прогноза с мнением эксперта
Инверсная верификация	Проверка адекватности прогнозной модели и объекта в ретроспективном периоде
Частичная целевая верификация	Построение условных подмоделей, эквивалентных полной модели, в типовых для проектируемой системы ситуациях
Структурная верификация	Сопоставление структур без экспериментальной проверки сопоставления в целом

Верификация модели – оценка ее функциональной полноты, точности и достоверности с использованием всей доступной информации в тех случаях, когда проверка адекватности по тем или иным причинам невозможна.

В прогнозировании чаще используют верификацию, так как в большинстве случаев реальный объект отсутствует или разрабатываются новые (еще не существующие) функции объекта прогнозирования. В табл.4.1 представлены наиболее часто используемые методы верификации.

В прогнозировании случай совершенного прогноза достигается крайне редко, поэтому проблема верификации прогнозной модели является одной из важнейших в прогностике. Степень совершенства прогнозов выражают через различные измерители точности прогнозирования. Точность точечного прогноза в момент t_i определяется разностью между прогнозом P_i и фактическим значением F_i прогнозируемого показателя в этот момент времени. Отдельный точечный прогноз не определяет точность конкретной процедуры прогнозирования в целом, то есть потребуется некоторая выборка {(P_i, F_i)},на основе которой рассчитывается значение некоторого измерителя точности прогнозирования.

Важность проблемы точности прогнозирования определяет важность анализа различных ее измерителей. В настоящее время нет достаточно полного исследования всевозможных критериев точности, что затрудняет оценивание возможностей различных моделей и опытаих применения в прикладных работах по прогнозированию конкретных процессов [40].

Для измерения точности прогнозирования можно использовать любой коэффициент парной корреляции между последовательностями прогнозных и фактических значений. Классический критерий точности прогнозирования – коэффициент корреляции Пирсона.

(4.1)

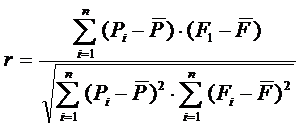
Максимальное значение r=1 достигается при наличии линейной связи между Р и F, т.е. когда существуют такие a₀ и a₁>0, что P=a₀ + a₁F.

Однако при a₀ ≠ 0 и a₁ = lпрогноз не будет совершенным, хотя корреляция полная и положительная; только при P = F коэффициент корреляции может характеризовать совершенный прогноз.

Коэффициент ранговой корреляции Спирмэна также может быть использован в качестве измерителя точности прогнозирования. Для этого вычисляются ранги {x_i} и {у_i} элементов соответствующих последовательностей {P_i} и {F_i}. Очевидно, что

(4.2)

.

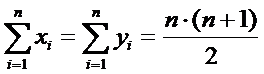Если несколько элементов из Pi или Fi имеют одинаковые ранги, то им определяется ранг, равный среднему арифметическому значений мест элементов в данной ранжировке. В этом случае последнее соотношение останется верным. Вычисляются корректирующие множители для связей соответственно для последовательностей{x_i} и {у_i}:

(4.3)

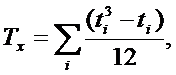
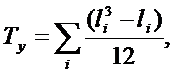
где t_i и l_i равно числу повторений i-го ранга в соответствующих последовательностях. Вычисляют сумму квадратов разностей рангов

(4.4)

.

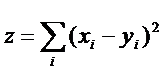Если T_x или T_y равно нулю, то коэффициент ранговой корреляции Спирмэна равен:

(4.5)

.

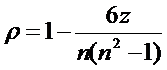Коэффициент ранговой корреляции r позволяет характеризовать качественную сторону последовательности прогнозов{P_i}, а именно способность предсказывать точки поворота. Коэффициент ранговой корреляции можно рассматривать как дополнительный измеритель точности прогнозирования при P_i=F_i и r, близким к 1, так как критерий ρ инвариантен относительно линейной вариации, причем при ρ = 1 прогноз может быть далеко не совершенным, так как для этого достаточно лишь совпадения рангов.

В качестве измерителей точности прогнозирования могут быть использованы и другие коэффициенты парной корреляции, например коэффициент ранговой корреляции Кендэлла. Однако для характеристики коэффициентов парной корреляции как некоторого класса измерителей точности прогнозирования достаточно провести анализ этих двух наиболее часто используемых коэффициентов, чтобы выделить общие для этого класса свойства. Во-первых, инвариантность относительно линейной вариации, а во-вторых, полная корреляция еще не определяют совершенный прогноз. Еще одним важным свойством коэффициентов парной корреляции является возможность проверки их на значимость, так как определены соответствующие законы распределения этих статистик. Например, для коэффициента ранговой корреляции Спирмэна значимость проверяется с п-2 степенями свободы по следующей t-статистике:

(4.6)

.

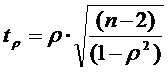Наиболее распространенными оценками точности прогнозирования также являются средняя ошибка аппроксимации

(4.7)

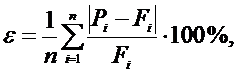
и средняя квадратическая ошибка прогнозов

(4.8)

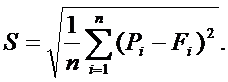
Точность прогнозирования тем выше, чем меньше значения e или S соответственно. Совершенный прогноз достигается при e=S=0.

Одним из исследователей проблем экономического прогнозирования, Г. Тейлом [40], предложен в качестве меры качества прогнозов коэффициент расхождения V (или коэффициент несоответствия), числителем которого является среднеквадратическая ошибка прогноза, а знаменатель равен квадратному корню из среднего квадрата реализации

(4.9)

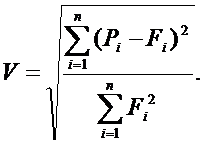
Если V=0, то прогноз абсолютно точен (случай «идеального» прогнозирования). Если V=1, то это означает, что прогноз близок к простой (и наивной) экстраполяции. Если V>1, то прогноз дает худший результат, чем предположение о неизменности тенденций исследуемого явления.

Коэффициент расхождения может быть использован при сопоставлении качества прогнозов, получаемых на основе различных методов и моделей. В этом его несомненное достоинство. Величина V поддается разложению на составляющие (частные коэффициенты расхождения), характеризующие влияние ряда факторов (это достигается разложением числителя, представляющего собой средний квадрат ошибки прогноза).

В некоторых случаях более важное значение имеют распознающие способности моделей прогнозирования, особенно при краткосрочном прогнозировании. Например, при прогнозировании выполнения месячных планов предприятий отрасли по особо учитываемой номенклатуре в начале месяца в первую очередь интерес представляет более точная оценка возможности выполнения плана, чем прогнозная информация о величине отклонения от плана. В данном случае целесообразно использовать следующую меру точности прогнозирования:

	(4.10)

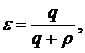
где q – число подтвержденных прогнозов;

r – число неподтвержденных прогнозов.

Если e =1, то имеет место случай «идеального» прогнозирования.

Таким образом, измерители точности прогнозирования по отношению к инвариантности относительно линейной вариации делятся на инвариантные и неинвариантные. Инвариантные измерители (S и коэффициенты парной корреляции), хотя и не позволяют сравнивать точность прогнозирования различных процессов, могут использоваться для определения точности прогнозирования различных последовательностей прогнозных значений {Рi} при фиксированной последовательности {Fi}. Например, подобная ситуация возникает при моделировании, когда необходимо выбирать между несколькими моделями прогнозирования, генерирующими соответствующие последовательности {Fi}. Инвариантные измерители могут быть проверены на статистическую значимость, то есть с определенной доверительной вероятностью конкретное значение измерителя является обоснованным. Однако особый интерес при построении моделей прогнозирования имеет критерий Г. Тейла, так как позволяет определить, в чем состоит расхождение: имеет место дрейф среднего или дрейф дисперсии. С другой стороны, критерий V не является инвариантным, и есть возможность оценивать применимость модели для совокупности различных прогнозируемых процессов в целом. Например, для прогнозирования по одной модели поведения отдельных предприятий или отрасли в целом.

Средняя ошибка аппроксимации e является наиболее наглядным измерителем точности прогнозирования, что вместе с неинвариантностью приводит к тому, что требование к точности задач прогнозирования формулируется по этому критерию.

Определить точность точечного прогноза по данным формулам можно при ретроспективности прогнозирования, когда апробируется модель, а также для прогнозов с ма­лым периодом упреждения (краткосрочные прогнозы).

Точность и надежность прогнозов – широко распространенные в прогностической литературе термины, смысл которых, как это представляется на первый взгляд, вполне очевиден. Однако содержание этих терминов часто толкуется достаточно субъективно. Нередки случаи, когда одно понятие подменяется другим ввиду отсутствия строгого определения данных категорий [48].

О точности прогноза принято судить по величине погрешности (ошибки) прогноза – разности между прогнозируемым и фактическим значением (реализацией) исследуемой переменной. Однако такой подход к оценке точности возможен только в двух случаях. Во-первых, когда период упреждения уже окончился и исследователь имеет фактические значения переменной. При краткосрочном прогнозировании это вполне реально. Во-вторых, когда прогноз разрабатывается ретроспективно, то есть прогнозирование осуществляется для некоторого момента времени в прошлом, для которого уже имеются фактические данные. Так поступают в тех случаях, когда проверяется разработанная методика прогноза.

При этом имеющаяся информация делится на две части. Одна из них, охватывающая более ранние данные, служит для оценивания параметров прогностической модели, а более поздние данные рассматриваются как реализации соответствующих прогностических оценок. Полученные ретроспективно ошибки прогноза в какой-то мере характеризуют точность примененной методики прогнозирования и могут оказаться полезными при сопоставлении нескольких методов. В то же время величину ошибки ретроспективного прогноза нельзя рассматривать как окончательное доказательство пригодности или, наоборот, непригодности применяемого метода прогнозирования. К ней следует относиться с известной осторожностью, и при ее применении в качестве меры точности необходимо учитывать, что она получена при использовании лишь части имеющихся данных. Однако эта мера точности обладает большей наглядностью и уж во всяком случае более надежна, чем погрешность прогноза, исчисленная для периода, характеристики которого уже были использованы при оценивании параметров модели. В последнем случае погрешности, как правило, будут незначительны и мало зависимы от теоретической обоснованности примененной для прогнозирования модели. Точность же прогнозов будет преувеличенной и в известном смысле иллюзорной.

Если для ретроспективного прогнозирования применяется модель, содержащая одну или несколько экзогенных переменных, то точность прогноза будет в значительной мере зависеть от того, насколько точно опреде­лены значения этих переменных на период упреждения. При этом возможны два пути: воспользоваться фактическими значениями экзогенных переменных (так называемый прогноз ex post) и ожидаемыми их значениями (так называемый прогноз ex ante). Естественно, что точность прогноза ex post будет выше, чем прогноза ex ante, так как в первом случае будет исключено искажающее влияние погрешности в значении экзогенных переменных. О степени погрешности прогноза можно судить по относительной ошибке – отношению абсолютной погрешности прогноза к ожидаемому (или фактическому) значению признака. Проверка точности единичного прогноза, как правило, мало что может сказать исследователю. В самом деле, на формирование исследуемого явления влияет множество разнообразных факторов, поэтому полное совпадение или значительное расхождение прогноза и его реализации может быть следствием просто особо благоприятных (или неблагоприятных) стечений обстоятельств. Единичный хороший прогноз может быть получен и по плохой модели, и наоборот. Отсюда следует, что о качестве прогнозов применяемых методик и моделей можно судить лишь по совокупности сопоставлений прогнозов и их реализации.

Измерители качества прогнозов (их точности) рассматривались выше при условии, что исследователь располагает информацией об истинных значениях величин, которые он оценивал в ходе разработки прогнозов. Такие меры качества, несомненно, представляют ценность при изучении различных методик прогнозирования. Однако в практической работе проблему точности прогноза надо решать тогда, когда период упреждения еще не прошел и истинное значение прогнозируемой переменной неизвестно. В этом случае проблема точности может рассматриваться в плане сопоставления априорных качеств, свойств, присущих альтернативным прогностическим моделям. Так, если прогнозирование осуществляется статистическими методами, то, вероятно, понятие точности прогноза можно сделать более узким, а именно связав априорную точность прогноза с размером доверительного интервала. Модель, дающая более узкий доверительный интервал при одной и той же доверительной вероятности, и является более точной (при этом теоретическая обоснованность сравниваемых моделей является примерно равной).

Очевидно, что надежность прогноза определяется вероятностью наступления прогнозируемого события, т.е. реализации соответствующей прогностической оценки. Чем она выше, тем выше и надежность. Вероятность реализации может быть оценена субъективно (экспертное прогнозирование) или может быть связана с доверительными интервалами прогноза, если последний основывается на статистической модели.

Рассмотренные понятия априорной точности и надежности прогнозов, связанные с доверительными интервалами, являются в значительной мере условными показателями. Они могут использоваться в практической работе лишь при условии, что принятая для получения прогнозов модель имеет серьезное теоретическое обоснование и спецификация модели корректна. В противном случае полученные доверительные интервалы лишь создают иллюзию точности. Практика разработки экономических прогнозов опирается на целую систему методов, среди которых статистические методы прогнозирования занимают важное место. Решающую роль при статистическом подходе к прогнозированию играет выбор соответствующей модели, которая, будучи наполненной числовыми параметрами, становится непосредственным инструментом прогнозирования – так называемым предиктором. Располагая предиктором, можно получить варианты прогноза, отвечающие определенным условиям и гипотезам, учтенным при его построении. Вместе с тем необходимо помнить, что механическое использование предиктора может стать причиной серьезных погрешностей.

Экономическое прогнозирование слишком ответственное дело, для того чтобы можно было ограничиться одними формальными построениями и расчетами. Цель модели – не заменить суждения и опыт специалиста, а дать ему в руки инструмент, позволяющий более глубоко проникнуть в существо исследуемых явлений, инструмент, в котором специфическим образом обобщена и приведена в систему разнообразная статистическая информация. Получаемые на основе предикторов прогнозы имеют смысл только в рамках тех условий, гипотез и предположений, которые были учтены при разработке соответствующих статистических моделей и при их применении для прогнозирования. Таким образом, разработка и применение моделей в прогностических целях предполагают углубленный экономический и экономико-статистический анализ.