От кратности выплаты купонного дохода

На рис. 5.5 приведены графики зависимости среднего срока поступлении дохода в зависимости от размера годовой купонной ставки, рассчитанные по формуле (5.13) при значениях 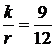и И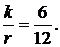з графиков видно, что увеличение годовой купонной ставки приводит к уменьшению среднего срока поступления дохода.

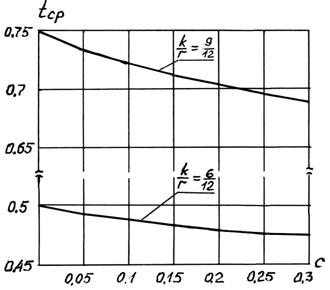
Рис. 5.5. Графики зависимости среднего срока поступления дохода

От размера годовой купонной ставки

Дюрация облигации

Рассмотрим вначале произвольный поток платежей:

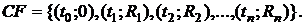
Для текущей стоимости потока (в момент времени t₀) относительно некоторой ставки доходности "у" можно записать:

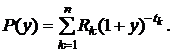
Продифференцируем данную функцию по "у":

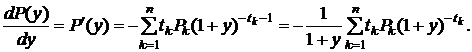(5.14)

Разделим обе части равенства (5.14) на Р(у) и получим:

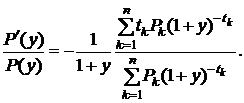(5.15)

Если ввести понятие весовых коэффициентов:

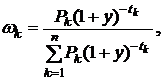(5.16)

то формулу (5.15) можно записать в виде:

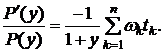(5.17)

Сомножитель 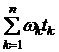аналогичен формуле (5.8) для среднего срока поступления дохода. Отличие состоит в том, что в данном случае весовые коэффициенты определяются по размерам платежей, дисконтированным к моменту времени t₀.

Этот сомножитель называется дюрацией потока платежей D:

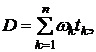(5.18)

где 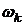определяется формулой (5.16).

Дюрация определяет средний срок поступления дохода с учетом временнόй стоимости денег, так как платежи дисконтируются к моменту времени t₀. В этом состоит преимущество данной характеристики финансового потока перед средним сроком поступления дохода.

Пример 5.1. Найти средний срок поступления дохода t_ср и дюрацию финансового потока:

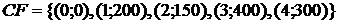при ставке доходности y = 12 %.

Решение: Для среднего времени поступления дохода по формуле (5.8) получим:

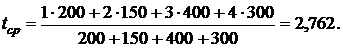
Для определения дюрации вычислим вначале дисконтированные размеры платежей:

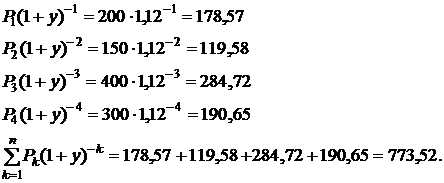
По формуле (5.16) вычислим весовые коэффициенты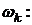

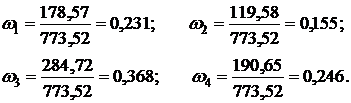
Сумма весовых коэффициентов должна быть равна единице:

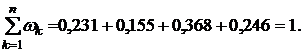
Теперь по формуле (5.18) можем вычислить значение дюрации финансового потока:

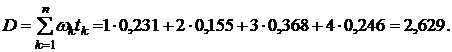
Из сравнения полученных результатов видно, что дюрация финансового потока меньше, чем средний срок поступления дохода.

Из формул (5.17) и (5.18) можно получить соотношение:

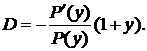(5.19)

Эта формула позволяет определить дюрацию облигаций.

Для облигации с выплатой купонного дохода по купонной ставке "с" номинальной стоимостью P_N при доходности облигации к погашению ρ ее текущая рыночная стоимость V определяется формулой (5.6).

Определим производную рыночной стоимости облигации по доходности к погашению:

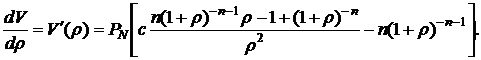
Вынесем общий множитель 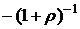за квадратные скобки и получим:

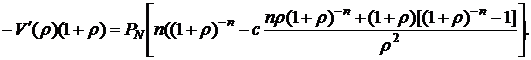
По аналогии с формулой (5.19) дюрацию облигации можно определить отношением:

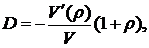(5.20)

где рыночная стоимость облигации V определяется формулой (5.6):

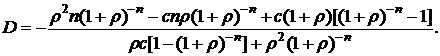
После несложных, но громоздких преобразований для дюрации облигаций получим:

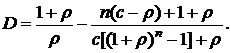(5.21)

1) Из формулы (5.21) видно, что для бескупонной облигации (с = 0) ее дюрация равна сроку до погашения облигации D = n.

2) Из формулы (5.20) видно, что относительные изменения рыночной цены облигации можно определить по приближенной формуле:

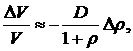(5.22)

где 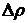- изменения доходности облигации к погашению.

3) Если облигация продается по номинальной стоимости 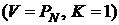, доходность к погашению равна купонной ставке и дюрация облигации определяется формулой:

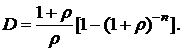
Определим зависимость дюрации облигации от ее параметров. На рис. 5.6 приведены графики зависимости дюрации облигаций от величины купонной ставки "с", рассчитанные по формуле (5.21) для двух значений срока до погашения облигации n = 4, n = 6 и для двух значений доходности к погашению 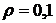и .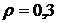

Из приведенных графиков видно, что увеличение купонной ставки и увеличение доходности облигации к погашению приводит к уменьшению дюрации.

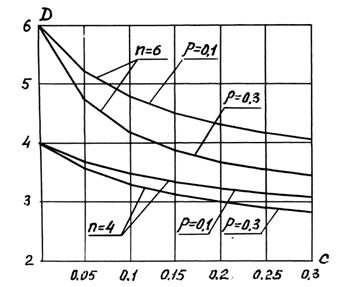
Рис. 5.6. Графики зависимости дюрации облигаций

от величины купонной ставки "с"

На рис. 5.7 приведены графики зависимости дюрации облигаций от срока до их погашения "n" при различных значениях доходности к погашению "ρ" и купонной ставки доходности "с". Кривая 1 рассчитана для значений 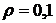и с = 0,2. Кривая 2 рассчитана для значений 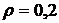и с = 0,1. Из формулы (5.21) и проведенных расчетов видно, что при увеличении срока до погашения облигации 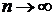второе слагаемое в формуле (5.21) стремится к нулю, и дюрация облигации приближается к значению .

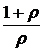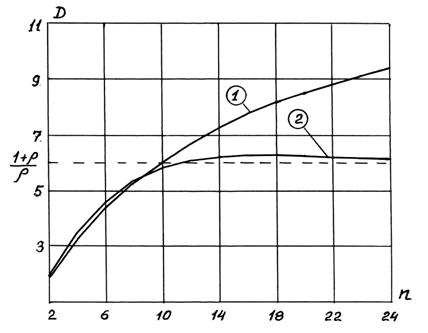
Рис. 5.7. Графики зависимости дюрации облигаций от срока до их погашения "n"

При 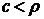график зависимости дюрации при увеличении "n" вначале пересекает асимптоту, а затем асимптотически сверху приближается к ее значению. График зависимости дюрации 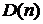пересекает асимптоту в точке, когда второе слагаемое в формуле (5.21) равно нулю, т. е. при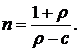

Таким образом, график зависимост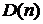и при 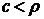имеет максимум, который может быть найден из условия равенства нулю производной 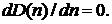Приближенное значение "n_о", при котором дюрация имеет максимальное значение при условии:

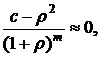
может быть записано в виде:

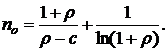
При и 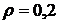дюрация имеет максимальное значение при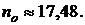

Выпуклость облигации

Понятие выпуклости облигаций вводят в соответствии с понятием выпуклости графика зависимости рыночной стоимости облигации V от ее доходности к погашению ρ – формула (5.6) и рис. 5.1

График функции V(ρ) является выпуклым вниз на некотором интервале, если вторая производная 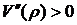положительна.

Выпуклость облигации определяют по формуле:

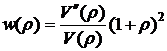. (5.23)

При вычислении второй производной удобнее воспользоваться формулой для V(ρ), аналогичной формуле (5.1):

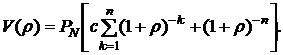(5.24)

После вычисления второй производной с учетом формулы (5.3) получим:

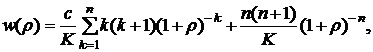(5.25)

где с – купонная ставка облигации;

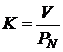- курс облигации.

Проведем определение выпуклости облигаций на примере двух облигаций: бескупонной облигации номинальной стоимостью 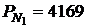руб. и сроком до погашения 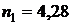лет и облигации номинальной стоимостью 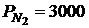руб. с купонной ставкой 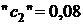и сроком до погашения 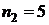лет.

В табл. 5.1 приведены результаты расчетов рыночной стоимости облигаций по формуле (5.24) для бескупонной облигаци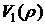и при 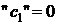и для второй облигации 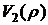при различных значениях доходности к погашению.

Таблица 5.1