Критерий Лапласа (равновозможностей).

1. Решающая функция: среднее значение выплаты по i-ой строке таблицы выплат:

.

2. Решающее правило: .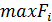

Критерий Лапласа выбирает решение, которому соответствует максимальное среднее значение выплаты (т.е. выбор наибольшего значения из ожидаемых выплат).

При использовании этого критерия все исходы для выбранной альтернативы (решения) принимаются равновероятными (отметим, что это субъективное суждение ЛПР). Далее мы можем оперировать этими равными вероятностями, как будто они на самом деле равны. Если так, то математическое ожидание результата выбранной альтернативы определяется как средняя арифметическая простая результатов (выплат). Довольно часто такой упрощенный подход оказывается привлекательным в практических ситуациях принятия решений.

4. Критерий Гурвица (взвешенный критерий оптимизма - пессимизма).

1. Решающая функция: сумма произведений некоторого параметра 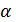и на величину максимальной и минимальной выплаты по i-ой строке соответственно:

.

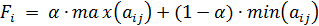2. Решающее правило: .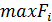

Параметр 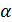- параметр оптимизма, выбор значения которого осуществляют эксперты на основе анализа текущего финансового состояния ЛПР или некоторых экономических показателей.

Значения параметра находятся в пределах 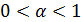: чем ближе 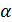к 1 или 100%, тем более оптимистично настроен и готов рисковать ЛПР, а его финансовое положение благополучно; чем ближе 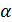к 0, тем более пессимистичен и не склонен к риску ЛПР, его финансовое состояние неудовлетворительное.

При 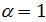критерий Гурвица превращается в критерий максимакс, т.е. ЛПР выбирает максимальную выплату из максимально возможных. Этот критерий также называют критерием азартного игрока или крайнего оптимизма. При a=0 он превращается в максимин, или критерий Вальда, т.е. критерий пессимиста.

Следует отметить, что при определении параметра 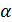речь идет не об объективных вероятностях того, или иного исхода, а именно о средней степени оптимистичности или, напротив, пессимистичности оценок, даваемых самим ЛПР. При этом на выбор влияют только самый лучший и самый худший исходы по каждой альтернативе.

Пример 4.1.

Фирма решает вопрос о сроках перехода к массовому выпуску нового вида продукции. Эта продукция является довольно дорогой, и потому на первых порах может не найти массового покупателя, поэтому излишняя торопливость может привести к тому, что выпущенная продукция не будет продана, а «осядет» на складах. Под ее остатки придется брать кредит в банке и платить за него проценты, что в конечном итоге может привести к убыткам. Но медлить тоже нежелательно, т.к. инициативу могут перехватить конкуренты, и тогда часть ожидаемой прибыли будет упущена.

Возможные последствия (прибыль/ убыток, тыс. у.е.) перехода к массовому выпуску новой продукции при разной реакции на нее рынка приведены ниже в таблице выплат. Найти оптимальный срок перехода к массовому производству нового вида продукции.

Переход к массовому производству	Срок наступления массового спроса
немедленно	через 1 год	через 2 года
немедленно			-6
через 1 год
через 2 года

Решение.

Выбор оптимального решения здесь затруднен отсутствием сведений о вероятностях той или иной реакции рынка. Поэтому используем критерии принятия решений в ситуации неопределенности.

1. Рассмотрим критерий Вальда. Для этого по каждому варианту решения определим наихудший результат :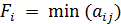

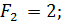
Согласно решающему правилу наилучший (максимальный) из худших результатов 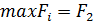, т.е. оптимальным является выбор перехода к массовому производству через один год.

2. Применим критерий Сэвиджа. Для этого на первом этапе находим наилучшие (максимальные) выплаты по каждому столбцу .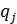

Переход к массовому производству	Срок наступления массового спроса
немедленно	через 1 год	через 2 года
Наилучшая выплата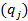

Это те максимальные выплаты, которые можно было бы получить, если бы удалось точно угадать возможную реакцию рынка.

Далее находим недополученные выгоды для каждого варианта решения и состояния среды . Полученные значения отклонений представим в виде матрицы рисков или сожалений.

Переход к массовому производству	Срок наступления массового спроса
немедленно	через 1 год	через 2 года
немедленно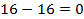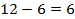
через 1 год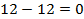
через 2 года		12-2=10

Элементы матрицы рисков – это недополученная прибыль от неудачно принятых решений из-за ошибочной оценки возможной реакции рынка.

На следующем этапе определим максимальное значение риска (недополученной прибыли) по каждому варианту решения :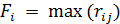

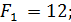
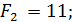
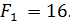
Согласно решающему правилу минимальное значение максимальных недополученных выплат 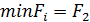, т.е. оптимальным является выбор перехода к массовому производству через один год.

3. Используем критерий Лапласа. Для этого по каждому варианту решения определим среднее значение выплаты :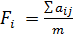

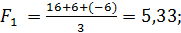
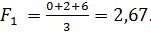
Согласно решающему правилу максимальное среднее значение выплаты 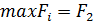, т.е. оптимальным является выбор перехода к массовому производству через один год.

4. Рассмотрим критерий Гурвица. Предположим, что по экспертным оценкам параметр оптимизма 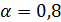, т.е. возможен выбор более рискованного решения. По каждому варианту решения определим взвешенную сумму максимальной и минимальной выплат :

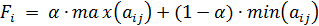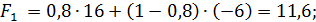
Согласно решающему правилу максимальное значение , т.е. оптимальным является выбор перехода к массовому производству немедленно.

Следует обратить внимание на то, что выбор рискованного варианта немедленного перехода к массовому производству обусловлен заданным параметром 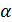, его снижение может привести к изменению стратегии на менее рискованную (например, переход к производству через год или два года).

Рассмотренные критерии применимы только для идеализированных практических решений (все состояния среды равновероятны, отсутствует конкуренция на рынке и т.п.).

В таком случае можно применять поочередно различные критерии, после чего среди нескольких вариантов, на которые указали критерии, ЛПР волевым методом выбирает окончательное решение. Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора.

Отдельно рассмотрим критерий произведений и взвешенный критерий произведений, условия использования которых отличаются от рассмотренных ранее учетом фактора времени.

Критерий произведений.

Отдельно рассмотрим ситуацию, когда выплаты для каждого варианта решения вычисляются не для различных состояний среды, а для различных моментов времени (табл.4.3).

Таблица 4.3

Общий вид таблицы выплат

Вариант решения	Моменты времени
T1	T2	…..	Tm
А1	a11	a12		a1m
А2	a21
…..
Аn	an1			anm

Здесь 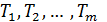– моменты времени, где – начальный и конечный моменты времени соответственно.

Для ситуаций, в которых важную роль играет фактор времени, используют критерий произведений. Критерий произведений применим только для случаев, когда все выплаты строго положительны. Он позволяет выбрать такой инвестиционный проект, который бы был наиболее доходным и в то же время наименее рискованным.

1. Решающая функция: произведение выплат по i-ой строке таблицы выплат:

.

2. Решающее правило: .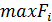

Критерий произведений выбирает решение, которому соответствует максимальное произведение выплат. Критерий произведений, в отличие от всех предыдущих, может использоваться в ситуациях, когда выплаты для каждого варианта решения вычисляются для различных состояний среды, и для различных моментов времени.

Отметим, что критерий произведений не совсем точно переводит показатели колеблемости в показатели надежности и обычно несколько завышает оценку риска потерь, т.е. он ориентирует инвестора на излишне осторожное поведение. Такое поведение может привести к упущенной прибыли, однако с точки зрения предупреждения возможных убытков оно является оправданным.