Постановка стохастической задачи

Разработать планы оптимальной системы финансовых портфелей банка не просто. Необходима слаженная работа целой группы квалифицированных специалистов: топ-менеджера, отвечающего за стратегию и управление финансовыми ресурсами банка, плановика или портфельного менеджера, задающего и корректирующего варианты планов портфелей, аналитика инструментов фондового рынка, аналитика-математика, обеспечивающего алгоритмическое решение оптимизационной задачи, и программиста, реализующего финансовые и математические идеи в виде программного обеспечения. Но даже при выполнении этих условий, т. е. наличия квалифицированных специалистов, при внедрении задач в банковскую деятельность встает вопрос: а будет ли вообще план полезен, если все время случайным образом меняется большинство параметров модели? Ответом на этот вопрос является постановка и решение задачи стохастического программирования, к рассмотрению которой мы переходим.

Рассмотрим, как следует составлять математическую модель задачи оптимизации для стохастической задачи. За основу возьмем модель линейного программирования:

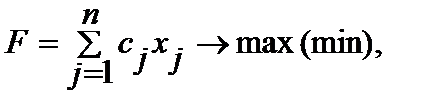(2.4.1)

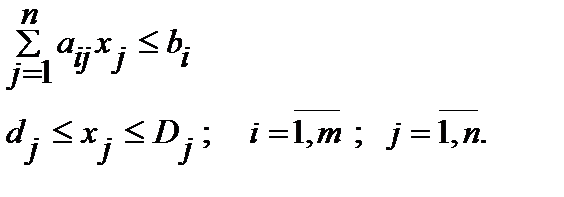(2.4.2)

Если коэффициенты 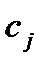в целевой функции – случайные величины, то возможны две постановки задачи оптимизации:

- максимизация (минимизация) среднего значения целевой функции, которая называется М-постановкой;

- максимизация вероятности получения максимального (минимального) значения, которая называется Р-постановкой:

Если случайными окажутся величины 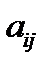и 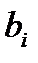, входящие в ограничения, то 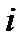-тое ограничение записывается так:

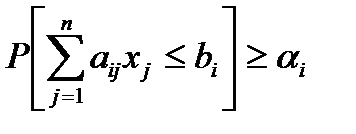, (2.4.3)

где 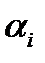– заданная вероятность, с которой должно быть выполнено ограничение.

Задача стохастического программирования в М-постановке

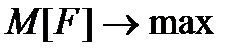(2.4.4)

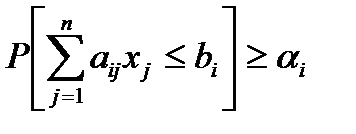(2.4.5)

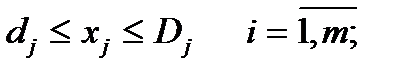
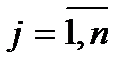
Для решения задачи следует перейти к ее детерминированному эквиваленту. В этом случае целевая функция записывается

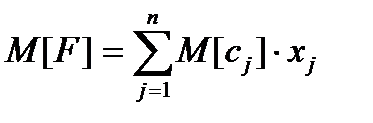. (2.4.6)

Детерминированный эквивалент ограничений имеет следующий вид:

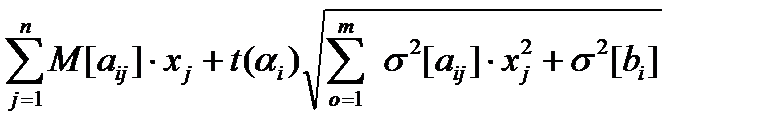
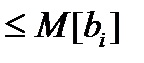, (2.4.7)

где 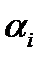– задаваемый уровень вероятности, с которой должно выполняться ограничение; 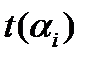– вычисляется с помощью функции от .

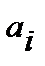Введем обозначение

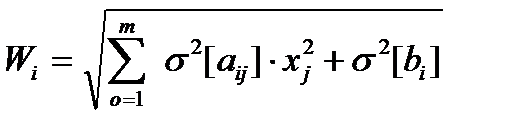. (2.4.8)

Тогда детерминированный эквивалент задачи выглядит следующим образом:

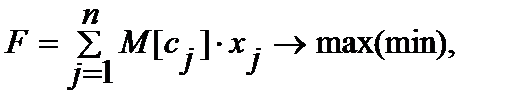(2.4.9)

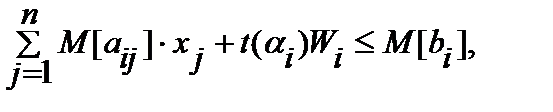(2.4.10)

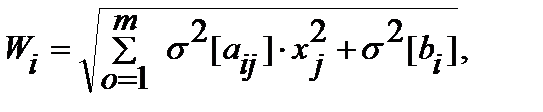(2.4.11)

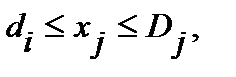(2.4.12)

.

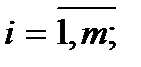
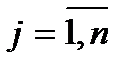Будем рассматривать ставшую уже классической стохастическую задачу оптимизации портфеля банка следующего вида:

Пр = П_ЦБ ЦБ + П_КР КР – И_ДВ ДВ – И_СД СД 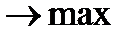; (2.4.13)

ЦБ + КР = ДВ + СД + К ; (2.4.14)

ЦБ + КР < 100 ; (2.4.15)

–0,7 ЦБ + 0,3 КР < 0 ; (2.4.16)

КР > 35 , (2.4.17)

где Пр – прибыль; ЦБ – ценные бумаги; КР – кредиты; ДВ – депозиты до востребования; СД – срочные депозиты; К – собственный капитал; П_ЦБ и П_КР – прибыль на ценные бумаги и кредиты соответственно; И_ДВ и И_СД – издержки по привлечению депозитов.

Алгоритм решения задачи стохастического программирования легко получить, используя приведенные выше соотношения, а также символику и методику решения задачи линейного программирования. При вводе исходных данных достаточно часто значения 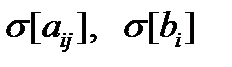бывают неизвестны. В этом случае можно задать коэффициент вариабельности 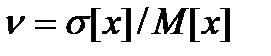и, зная который, определить

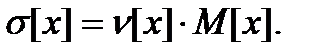(2.4.18)