Операции со сложной учетной ставкой

Здесь, как и в случае простых процентов, рассмотрим два вида учета: математический и банковский.

Математический учет. В этом случае решается задача, обратная наращению по сложным процентам, т.е. задача определения P по значению S при заданной ставке процента. На основе формулы (2.1) получим:

,

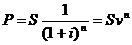где vⁿ=(1+i)^-n – учетный или дисконтный множитель.

Для случаев, когда проценты начисляются m раз в году, получим:

,

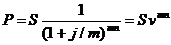где v^mn=(1+j/m)^-mn – дисконтный множитель.

Величину P называют современной или текущей стоимостью или приведенной величиной S. Современная стоимость может быть рассчитана на любой момент до выплаты суммы S. Суммы P и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Разность D=S-P, когда P определено дисконтированием, называют дисконтом, т.е. D=S-P=S(1-vⁿ)

Пример 16. Сумма в 5 тыс. ден. ед. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов, равная 15% годовых.

Решение. Дисконтный множитель для данных условий составит v⁵=1/(1+0,15)⁵= =0,49718, т.е. первоначальная сумма сократилась почти на 50%. Современная величина равна P=5000·0,49718=2485,90 ден. ед.

Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

P=S(1-d_сл)ⁿ, (2.3)

где d_сл – сложная годовая учетная ставка. Дисконт в этом случае равен D=S-P= =S(1-(1-d_сл)ⁿ).

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Пример 17. Долговое обязательство на сумму 5 тыс. ден. ед., срок оплаты которого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15% годовых. Каков размер полученной за долг суммы и величина дисконта?

Решение. Полученная за долг сумма (современная величина) равна

P=5000·(1-0,15)⁵=5000·0,4437=2218,53 ден. ед.

Дисконт составил D=S-P=5000-2218,53=2781,47 ден. ед.

Если же применить простую учетную ставку того же размера, то

P=5000·(1-5·0,15)=1250 ден. ед.; дисконт составит 5000-1250=3750 ден. ед.

Номинальная и эффективная учетные ставки процентов. В тех случаях, когда дисконтирование применяют m раз в году, используют номинальную учетную ставку f. Тогда в каждом периоде, равном 1/m части года, дисконтирование осуществляется по сложной учетной ставке f/m. Процесс дисконтирования по этой сложной учетной ставке m раз в году описывается формулой

P=S(1-f/m)^N, (2.4)

где N – общее число периодов дисконтирования (N=mn).

Дисконтирование не один, а m раз в году быстрее снижает величину дисконта.

Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m. Найдем связь эффективной процентной ставки с номинальной из равенства дисконтных множителей:

(1-f/m)^mn=(1-d_сл)ⁿ,

из которого следует, что

d_сл=1-(1-f/m)^m.

В свою очередь,

f=m(1-(1-d_сл)^1/m)

Эффективная учетная ставка во всех случаях, когда m>1, меньше номинальной ставки (для одинаковых периодов).

Пример 18. Долговое обязательство на сумму 5 тыс. ден. ед., срок оплаты которого наступает через 5 лет, продано с дисконтом. Определить сумму, полученную при поквартальном учете по номинальной учетной ставке 15%, и эффективную учетную ставку.

Решение. f=0,15; m=4; mn=20;

Полученная за долг сумма составит P=5000·(1-0,15/4)²⁰=5000·0,4656=2328 ден. ед.

Эффективная учетная ставка составит d_сл=1-(1-0,15/4)⁴=0,14177, или 14,177%

Наращение по сложной учетной ставке. Наращение является обратной задачей для учетных ставок. Формулы наращения можно получить, разрешая соответствующие формулы для дисконтирования (2.3 и 2.4) относительно S:

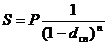или .

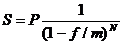Пример 19. Какую сумму следует проставить в векселе, если реально выданная сумма равна 20 тыс. ден. ед., срок погашения – 2 года. Вексель рассчитывается, исходя из сложной годовой учетной ставки 10%, и наращение осуществляется: (1) один раз в год; (2) 4 раза в год.

Решение. (1) S=20000/(1-0,1)²=20000/0,81=24691,36 ден. ед.

(2) S=20000/(1-0,1/4)⁸=20000/0,816652=24490,24 ден. ед.

Непрерывные проценты

В практических финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при обосновании и выборе инвестиционных решений.

Наращенная сумма при дискретных процентах определяется по формуле

S=P(1+j/m)^mn,

где j – номинальная ставка процентов, а m – число периодов начисления процентов в году.

Чем больше m, тем меньше промежутки времени между моментами начисления процентов. Увеличение частоты начисления процентов (m) при фиксированном значении номинальной процентной ставки j приводит к росту множителя наращения, который при непрерывном начислении процентов (m®¥) достигает своего предельного значения

(2.5)

Известно, что

,

где е – основание натуральных логарифмов.

Используя этот предел в выражении (2.5), окончательно получаем, что наращенная сумма по ставке j равна

S=Pe^jn.

Непрерывную ставку процентов называют силой роста и обозначают символом d. Тогда

S=Pe^dn. (2.6)

Сила роста d представляет собой номинальную ставку процентов при m®¥.

Закон наращения при непрерывном начислении процентов (2.6) совпадает по форме с (2.2) с той разницей, что в (2.2) время изменяется дискретно с шагом 1/m, а в (2.6) – непрерывно.

Легко показать, что дискретные и непрерывные ставки наращения находятся в функциональной зависимости. Из равенства множителей наращения можно получить формулу эквивалентного перехода от одних ставок к другим:

(1+i)ⁿ=e^dn,

откуда следует:

d=ln(1+i), i=e^d-1.

Пример 20. Сумма, на которую начисляются непрерывные проценты в течение 5 лет, равна 2000 ден. ед., сила роста 10%. Наращенная сумма составит S=2000·e^0,1·5=2000·1,6487=3297,44 ден. ед.

Непрерывное наращение по ставке 10% равнозначно наращению за тот же срок сложных дискретных процентов по годовой ставке i. Находим:

i=e^0,1-1=1,10517-1=0,10517.

В итоге получим S=2000·(1+0,10517)⁵=3297,44 ден. ед.

Дисконтирование на основе силы роста осуществляется по формуле

P=Se^-dn

Пример 21. Определим современную стоимость платежа из примера 17 при условии, что дисконтирование производится по силе роста 15%.

Решение. Полученная за долг сумма (современная величина) равна

P=5000·е^-0,15·5=5000·0,472366=2361,83 ден. ед.

При применении дискретной сложной учетной ставки такого же размера получили величину (см. пример 17) P=2218,53 ден. ед.