Приведенная стоимость аннуитета при начислении процента один раз в год

Приведенная стоимость аннуитета представляет собой будущую стоимость аннуитета, дисконтированную к моменту времени его учреждения, т. е. на величину

Приведенная стоимость аннуитета равна:

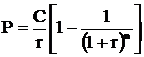
где Р– приведенная стоимость аннуитета.

Формулу приведенной стоимости аннуитета также можно использовать в случае, когда заемщик берет кредит на условиях его погашения в будущем равными платежами ежегодно. Для этого найдем С:

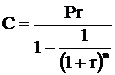
где: Р– сумма кредита;

r – процент по кредиту;

С– платеж по кредиту;

n – число лет, на которые берется кредит.

Приведенная стоимость аннуитета при осуществлении выплат т раз в год.

Для рассматриваемого случая приведенную стоимость аннуитета находят дисконтированием будущей стоимости аннуитета на

Тогда:

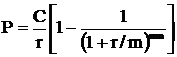
5.2.3. Приведенная стоимость аннуитета при начислении процента т раз в год:

Вечная рента

Вечная рента предполагает, что платежи будут осуществляться всегда. Будущую стоимость такого аннуитета определить невозможно, так как она не являет конечной величиной. Однако можно рассчитать приведенную стоимость вечной ренты. Поскольку для такого аннуитета п→∞, то она принимает вид:

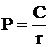
Примером вечного аннуитета может служить английская бессрочная государственная облигация, которая называется консоль. Она выпущена в 18 веке и по ней выплачивается доход каждые полгода.

Немедленный аннуитет

На рынке ценных бумаг главным образом используется понятие отложенного аннуитета. Поэтому приведем формулы будущей и приведенной стоимости немедленного аннуитета только для случая начисления сложного процента один раз в год.

где:F_n – будущая стоимость немедленного аннуитета;

n– количество лет, в течение которых выплачивается аннуитет.

Приведенную стоимость немедленного аннуитета найдем дисконтированием правой части формулы на (1+r)ⁿ.

Тогда

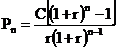
где: Р_n – приведена стоимость немедленного аннуитета.

Приведенная стоимость немедленной вечной ренты:

ДОХОДНОСТЬ

На финансовом рынке инвестора интересует результативность его операций.

Например, лицо А инвестировало 2 млн. руб. на три года и получило сумму в 6 млн. руб. Лицо В инвестировало 3 млн. руб. на пять лет, и его результат составил 10 млн. руб. Какой из вариантов инвестирования оказался более предпочтительным. Ответить на данный вопрос с помощью абсолютных величин довольно трудно, так как в примере отличаются как суммы, так и сроки инвестирования. Результативность инвестиций сравнивают с помощью такого показателя как доходность. Доходность – это относительный показатель, который говорит о том, какой процент приносит рубль инвестированных средств за определенный период. Например, доходность инвестиций составляет 10%. Это означает, что инвестированный рубль приносит 10 коп. прибыли. Более высокий уровень доходности означает лучшие результаты для инвестора.

В самом общем виде показатель доходности можно определить как отношение полученного результата к затратам, которые принесли данный результат. Доходность выражают в процентах. Когда мы рассматривали вопросы начисления процентов, то оперировали определенными процентными ставками. Данные процентные ставки есть не что иное как показатели доходности для операций инвесторов. В финансовой практике принято, что показатель доходности или процент на инвестиции обычно задают или определяют в расчета на год, если специально не сказано о другом временном периоде. Поэтому, если говорится, что некоторая ценная бумага приносит 20%, то это следует понимать, как 20% годовых. В то же время реально бумага может обращаться на рынке в течение времени больше или меньше года. Такая практика существует потому, что возникает необходимость сравнивать доходность инвестиций, отличающихся по срокам продолжительности. Рассмотрим некоторые разновидности показателя доходности.

Доходность за период

Доходность за период – это доходность, которую инвестор получит за определенный период времени. Она определяется по формуле:

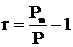
где: r– доходность за период;

Р– первоначально инвестированные средства;

P_n– сумма, полученная через п лет.

Доходность в расчете на год

На финансовом рынке возникает необходимость сравнивать доходности различных финансовых инструментов. Поэтому наиболее часто встречающийся показатель доходности – это доходность в расчета на год. Он определяется как средняя геометрическая, а именно:

где: r – доходность в расчете на год;

n – число лет.

Если сложный процент начисляется т раз в год, то доходность за год определяется на формуле:

Если процент начисляется непрерывно, то доходность в расчете на год можно определить по формуле:

где: r_n – доходность, представленная как непрерывно начисляемый процент.

Для краткосрочных операций доходность определяется как:

Для краткосрочных ценных бумаг также можно рассчитать эффективную доходность, т.е. эффективный процент. Для этого можно воспользоваться следующей формулой:

или

где: r_эф – эффективная доходность в расчете на год;

t – период финансовой операции (время с момента покупки до продажи или погашения ценной бумаги);

r – простой процент в расчете на год;

r_t– доходность за период t.