Обобщающие параметры потоков платежей
Тема 2. Потоки платежей
Краткое содержание раздела:
Понятие финансового потока. Приведенная и наращенная величины финансового потока. Средний срок финансового потока. Непрерывные потоки платежей.
Регулярные потоки платежей. Обыкновенные ренты. Ренты постнумерандо и пренумерандо. Коэффициенты приведения и наращения рент. Связь между приведенной величиной и наращенной суммой аннуитета. Связь между коэффициентами приведения и наращения рент пренумерандо и постнумерандо.
Расчет параметров ренты.
Вечные, кратные, срочные ренты. р – срочная рента (случаи k = 1, 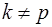 , k = p ). Связь между приведенной и наращенной величинами p – срочной ренты (случаи k = 1,
, k = p ). Связь между приведенной и наращенной величинами p – срочной ренты (случаи k = 1, 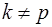 , k = p ). Непрерывные ренты. Связь между приведенной и наращенной величинами произвольных рент.
, k = p ). Непрерывные ренты. Связь между приведенной и наращенной величинами произвольных рент.
Сравнение финансовых потоков и рент. Общий принцип сравнения финансовых потоков и рент. Сравнение годовых и срочных рент. Конверсия рент. Замена одной ренты другой. Изменение параметров ренты. Замена обычной ренты срочной. Консолидация рент. Выкуп ренты. Рассрочка платежа.
2.1. Потоки платежей
Современные финансово-банковские операции часто предполагают не разовые платежи, а некоторую их последовательность во времени. Примеры: погашение задолженности в рассрочку, выплата пенсии, взносы на расчетный счет и др. Такого рода последовательности называют потоками платежей.
Поток платежей, все члены которого положительны, а временные интервалы между платежами одинаковы, называют финансовой рентой или аннуитетом.
Виды рент:
1) обычная годовая – платежи поступают один раз в год,
2) р-срочная – платежи поступают р раз в году,
3) верные и условные (например, кредит – верная рента, пенсия – условная),
4) немедленные, отложенные, отсроченные – отличаются по началу выплат,
5) пренумерандо (выплаты в начале периода) и постнумерандо (выплаты в конце периода).
Основные характеристики рент;
- член ренты R – размер отдельного (годового) платежа,
- период ренты – временной интервал между последовательными платежами (число платежей в году – p, количество начислений процентов в году – m),
- срок ренты n – время от начала первого периода ренты до конца последнего,
- процентная ставка i (j).
Решение.
| A=200 млн.руб. |  |
| n=4 | 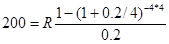 |
| j=20 % | 200=R*2.71 |
| m=p=4 | R=200/2.71=73.8 (млн.руб. в год) |
| R/4 | R/4=73.8/4=18.45 (млн.руб. в квартал) |
Пример (билет № 18).В течение 5 лет в конце каждого полугодия на расчетный счет поступают равными долями платежи из расчета 8 млн.руб. в год, на которые ежеквартально начисляются проценты из расчета 20 % годовых. Требуется определить сумму на расчетном счете к концу указанного срока. Найти размер платежей, при которых эта же сумма на расчетном счете образуется за 4 года.
Решение.
| n=5 | 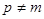 |
| p=2 | 1) 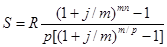 |
| R=8 млн.руб. | 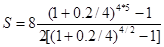 =64.5 (млн.руб.) =64.5 (млн.руб.) |
| m=4 | 2)  |
| j=20 % | 64,5=  *5,77 *5,77 |
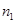 =4 =4 |  =64,5/5,77=11,1785 (млн.руб. в год) =64,5/5,77=11,1785 (млн.руб. в год) |
| 1) S | |
2)  |
Пример (билет № 9)*.Фирма в качестве компенсации работникам за причиненный им ущерб должна выплатить 100 млн. руб. в течение 25 лет. Платежи должны производиться равномерно в течение этого периода – в конце каждого квартала. Найти реальную (современную) стоимость данной компенсации для фирмы, если принять годовую ставку сложных процентов на уровне 10 %.
Решение.
| S=100 млн.руб. | 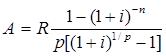 , , |
| n=25 | R=S/n=100/25=4 (млн.руб. в год) |
| p=4 |  =37,6427 (млн.руб) =37,6427 (млн.руб) |
| i=10 % | |
| A-? | Вывод: капитал в сумме 37,6 млн.р. при начислении 10 % годовых достаточен для выплаты компенсации. |
2.2. Практические приложения
Актуарный метод
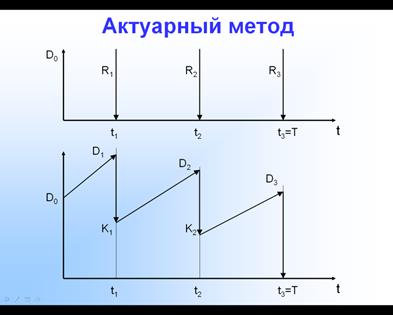
Ссуда 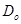 выдана на период Т, в течение которого предполагаются 2 промежуточных платежа:
выдана на период Т, в течение которого предполагаются 2 промежуточных платежа:
1) за период [0, 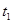 ] сумма выросла до
] сумма выросла до 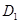 ; в момент времени
; в момент времени 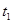 вносится первый платеж
вносится первый платеж  , который включает проценты и часть основного долга; остаток долга –
, который включает проценты и часть основного долга; остаток долга – 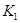 =
= 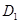 -
-  ;
;
2) за период [ 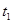 ,
,  ] сумма выросла до
] сумма выросла до 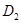 ; в момент времени
; в момент времени  вносится второй платеж
вносится второй платеж 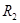 , который включает проценты и часть основного долга; остаток долга –
, который включает проценты и часть основного долга; остаток долга –  =
= 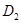 -
- 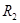 ;
;
3) за период [  ,
, 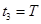 ] сумма выросла до
] сумма выросла до 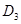 ; в момент времени
; в момент времени 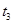 вносится последний платеж
вносится последний платеж 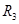 =
= 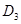 , который погашает весь долг.
, который погашает весь долг.
Если долга обнуляется, то операция называется сбалансированной,а ее контур является замкнутым.
Правило торговца
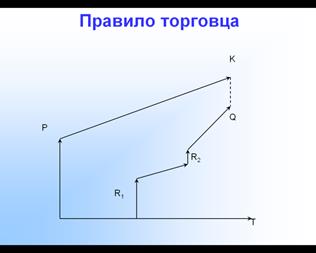
Решение.
| Р=100 тыс. руб. | 1) актуарный метод: |
| i=15 % (простая) | а) долг с % до 1 платежа: |
| n=6 мес. | 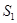 =100*(1+2,5/12*0,15)=103,125 (т.р.); I=103.125-100=3.125<60 =100*(1+2,5/12*0,15)=103,125 (т.р.); I=103.125-100=3.125<60 |
[0, 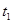 ]=2.5 мес. ]=2.5 мес. | б) остаток долга после 1 платежа: |
 =60 тыс.руб. =60 тыс.руб. |  = = 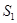 -60=103,125-60=43,125 (т.р.) -60=103,125-60=43,125 (т.р.) |
[ 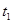 , ,  ]=2 мес. ]=2 мес. | в) долг с % до 2 платежа: |
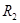 =1 тыс.руб. =1 тыс.руб. | 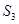 =43,125*(1+2/12*0,15)=44,2031 (т.р.); I=44.203-43.125=1.078>1 =43,125*(1+2/12*0,15)=44,2031 (т.р.); I=44.203-43.125=1.078>1 |
[  ,n]=1.5 мес. ,n]=1.5 мес. | г) 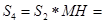 43.125*(1+(2+1,5)/12*0.15)=45.012 43.125*(1+(2+1,5)/12*0.15)=45.012 |
д) 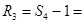 45,012-1=44,012 (т.р.) 45,012-1=44,012 (т.р.) | |
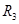 | |
| 2) правило торговца: | |
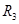 = 100*(1+6/12*0,15) - 60*(1+3,5/12*0,15) - % на всю сумму 1 платеж с начисл. % до к. ср. за весь период = 100*(1+6/12*0,15) - 60*(1+3,5/12*0,15) - % на всю сумму 1 платеж с начисл. % до к. ср. за весь период | |
| 1*(1+1,5/12*0,15) = 43,8563 (т.р.) | |
| 2 платеж с начисл. до конца срока % |
* Работа кредитного калькулятора
Решение.
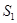 =2000 р. =2000 р. | Уравнение эквивалентности |
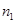 =2 =2 | 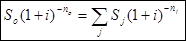 |
 =4000 р. =4000 р. | 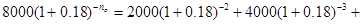 |
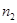 =3 =3 | 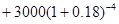 |
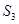 =3000 р. =3000 р. |  |
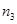 =4 =4 |  |
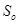 =8000 р. =8000 р. | 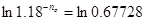 |
| i=18% | 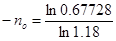 |
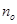 | 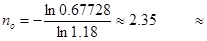 2 г. 4 мес. 2 г. 4 мес. |
Тема 2. Потоки платежей
Краткое содержание раздела:
Понятие финансового потока. Приведенная и наращенная величины финансового потока. Средний срок финансового потока. Непрерывные потоки платежей.
Регулярные потоки платежей. Обыкновенные ренты. Ренты постнумерандо и пренумерандо. Коэффициенты приведения и наращения рент. Связь между приведенной величиной и наращенной суммой аннуитета. Связь между коэффициентами приведения и наращения рент пренумерандо и постнумерандо.
Расчет параметров ренты.
Вечные, кратные, срочные ренты. р – срочная рента (случаи k = 1, 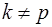 , k = p ). Связь между приведенной и наращенной величинами p – срочной ренты (случаи k = 1,
, k = p ). Связь между приведенной и наращенной величинами p – срочной ренты (случаи k = 1, 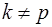 , k = p ). Непрерывные ренты. Связь между приведенной и наращенной величинами произвольных рент.
, k = p ). Непрерывные ренты. Связь между приведенной и наращенной величинами произвольных рент.
Сравнение финансовых потоков и рент. Общий принцип сравнения финансовых потоков и рент. Сравнение годовых и срочных рент. Конверсия рент. Замена одной ренты другой. Изменение параметров ренты. Замена обычной ренты срочной. Консолидация рент. Выкуп ренты. Рассрочка платежа.
2.1. Потоки платежей
Современные финансово-банковские операции часто предполагают не разовые платежи, а некоторую их последовательность во времени. Примеры: погашение задолженности в рассрочку, выплата пенсии, взносы на расчетный счет и др. Такого рода последовательности называют потоками платежей.
Поток платежей, все члены которого положительны, а временные интервалы между платежами одинаковы, называют финансовой рентой или аннуитетом.
Виды рент:
1) обычная годовая – платежи поступают один раз в год,
2) р-срочная – платежи поступают р раз в году,
3) верные и условные (например, кредит – верная рента, пенсия – условная),
4) немедленные, отложенные, отсроченные – отличаются по началу выплат,
5) пренумерандо (выплаты в начале периода) и постнумерандо (выплаты в конце периода).
Основные характеристики рент;
- член ренты R – размер отдельного (годового) платежа,
- период ренты – временной интервал между последовательными платежами (число платежей в году – p, количество начислений процентов в году – m),
- срок ренты n – время от начала первого периода ренты до конца последнего,
- процентная ставка i (j).
Обобщающие параметры потоков платежей
В подавляющем числе практических случаев анализ потока платежей предполагает расчет одной из двух обобщающих характеристик:
- наращенной суммы;
- современной стоимости потока.
Наращенная сумма S (будущая стоимость потока)– это сумма всех членов потока платежей с начисленными на них к концу срока процентами.
Под современной стоимостью потока платежей A (текущая стоимость потока)понимают сумму всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.
Сама по себе процедура дисконтирования является нетривиальной. Еще сложнее вопрос с операцией дисконтирования или нахождения текущей стоимости потока платежей. Смысл современной величины потока: это та начальная сумма, вложив которую под те же проценты и на то же количество лет, можно выплатить из нее все рентные платежи. Иными словами – это сегодняшний эквивалент всех будущих платежей потока.
Приведем теперь рядформулдля расчета будущей и текущей стоимостей потока при различных условиях контрактов:

Приведенные в таблице формулы соответствуют ренте постнумерандо. Формулы для ренты пренумерандо имеют отличия, связанные с начислениями за первый период:
1) для обычной годовой ренты получим:
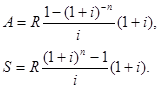
2) для обычной годовой ренты c начислением процентов m раз в году:
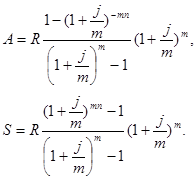
3) для р-срочной ренты с начислением процентов m раз в году:
| m=1 | m=p | 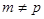 |
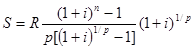 | 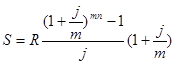 |  |
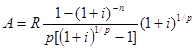 | 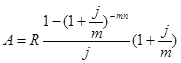 | 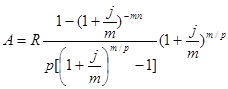 |
Вывод формул см. в П.Н. Брусов и др., пп. 2.5.2.3, 2.5.6.1 и др.
