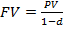Понятие процента, процентных денег и процентных ставок

Процентные деньги (или кратко проценты) - абсолютная величина дохода от предоставления денег в долг в любой его форме: выдача ссуды, продажа товара в кредит, помещение денег на депозитный счет, учет векселя, покупка сберегательного сертификата или облигации и т.д.

Относительным показателем характеризующим интенсивность начисления процентов за ед. времени является процентная ставка.

Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени – отношение дохода (процентных денег) к сумме долга (величине ссуды). Выражается либо в долях единицы, либо в процентах. Т.о. процентная ставка показывает, сколько денежных единиц должен заплатить заемщик за пользование в течение определенного периода времени 100 единицами первоначальной суммы долга.

Начисление процентов, как правило производится дискретно, т.е. за фиксированные одинаковые интервалы времени, которые называются период начисления.

Период начисления - это отрезок времени между двумя следующими друг за другом процедурами взимания процентов (или временной интервал, к которому приурочена процентная ставка).

Обычные или декурсивные проценты (postnumerando) начисляются в конце периода начисления.

В качестве периода времени (начисления) в финансовых расчетах как правило принимается год, однако это не исключает использование периода менее года (полугодие, квартал, месяц, день, час).

Увеличение суммы долга в связи с присоединением к ней процентных денег называется наращением, а увеличенная сумма – наращенной суммой.

Коэффициент наращения (или множитель наращения) – отношение наращенной суммы к первоначальной сумме долга.

Определение настоящей стоимости будущей суммы денег называется дисконтированием. В этом случае сумма денег, относящаяся к будущему, уменьшается на величину соответствующего дисконта (скидки).

В финансовом анализе процентная ставка применяется не только как инструмент наращения суммы долга, но и в более широком смысле – как измеритель степени доходности (эффективности) любой финансовой, кредитной, инвестиционной деятельности.

Виды процентных ставок:

Простая процентная ставка - применяется к одной и той же первоначальной сумме долга на протяжении всего срока ссуды, т.е. исходная база (денежная сумма) всегда одна и та же.

Сложная процентная ставка - применяется к наращенной сумме долга, т.е. к сумме увеличенной на величину начисленных за предыдущий период процентов. Т.о. исходная база начисления процентов постоянно увеличивается (процент начисляется на полученную на предыдущем этапе наращения или дисконтирования сумму – проценты начисляются на проценты).

При расчете процентных денег от настоящего к будущему применяются ставки наращения.

При расчете процентных денег от будущего к настоящему применяются ставки дисконтирования или учетные ставки.

Проценты, полученные по ставке наращения, называются декурсивными.

Проценты, полученные по учетной ставке, называются антисипативными.

Постоянная процентная ставка – неизменная на протяжении всего периода ссуды.

Переменная процентная ставка – дискретно изменяющаяся во времени, но имеющая конкретную числовую характеристику (указывается базовая ставка и размер надбавки к ней – маржи).

Важное место в системе процентных ставок занимает ставка рефинансировния Центрального банка РФ – ставка, по которой ЦБ выдает кредиты коммерческим банкам.

Простые проценты

Формула простых процентов

Процесс наращения – это процесс определения денежной суммы в будущем, исходя из заданной суммы сейчас.

Экономический смысл операции наращения – определении величины той суммы, которой будет располагать или желает располагать инвестор по окончании операции наращения.

При предоставлении денег в долг их владелец получает доход в виде процентов. При этом выделяется некоторый основной интервал времени, который называется базовым. На практике в качестве базового интервала часто берется год (стандартный временной интервал в финансовых вычислениях) и процентная ставка устанавливается в виде годовой ставки. Подразумевающей однократное начисление процентов по истечение года после получения ссуды.

PV – сегодняшняя стоимость денег;

FV - будущая стоимость сегодняшней суммы денег (PV);

r – ставка процентов (в десятичных дробях);

n – число лет на которое выдана ссуда.

PV

FV

n

t (время)

Сумма начисленных процентов (абсолютный прирост денег) (I) за 1 год:

I=FV-PV

Сумма начисленных процентов за ряд лет n (произведение абсолютных приростов на количество лет ссуды)

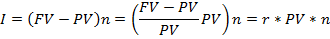
где 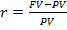– ставка процентов.

Т.о. размер ожидаемого дохода зависит от трех факторов:

- величина инвестированной суммы (PV),

-уровень процентной ставки (r),

- срок финансовой операции (n).

Определение наращенной суммы по схеме простых процентов (формула простых процентов)

FV=PV+I=PV+PV*r*n=PV(1+r*n)=PV*k_n,

где k_n = 1+r*n – множитель (коэффициент) наращения простых процентов.

К простым процентам прибегают в случаях:

- выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году, либо меньше его, с однократным начислением процентов;

- когда проценты не присоединяются к сумме долга, а периодически выплачиваются.

Формула простых процентов для случая, если срок ссуды (n) выражается в месяцах (М):

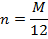
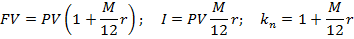
Формула простых процентов для случая, если срок ссуды (n) выражается в днях (t)

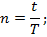
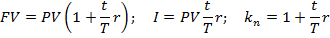
где t – число дней ссуды, т.е. продолжительность срока, на который выдана ссуда;

Т – расчетное число дней в году (временная база).

Временную базу (Т) можно представить по разному:

- как условно состоящую из 360 дней. В этом случае речь идет об обыкновенном или коммерческом проценте;

- как состоящую из действительного числа дней в году (365 или 366). В этом случае получают точный процент.

Определение числа дней ссуды (t):

- приближенное число дней ссуды получают тогда, когда исходят из того, что продолжительность любого месяца составляет 30 дней;

- точное число дней ссуды получают тогда, когда рассчитывают фактическое число дней между датой выдачи ссуды и датой возврата ссуды с использованием прямого счета или специальных таблиц порядковых номеров дней года.

Т.о. если время финансовой операции выражено в днях, то расчет простых процентов может быть произведен одним из трех способов:

1. Германская практика расчета (Германия, Дания, Швеция) – обыкновенные проценты (продолжительность года принимается равной 360 дням) с приближенным числом дней ссуды (продолжительность целого месяца принимается равной 30 дням( (360/360)

2. Французская практика расчета (Франция, Бельгия, Испания, Швейцария) - обыкновенные проценты (--//-- 360 дней) с точным числом дней ссуды (продолжительность ссуды рассчитывается точно по календарю) (360/365)

3. Английская практика расчета (Англия, США. Португалия) – продолжительность года и продолжительность ссуды берутся точно по календарю (365/365)

В зависимости от использоваия конкретной практики начисления простых процентов их сумма будет различаться по абсолютной величине. Результат финансовой операции зависит т выбора способа начисления простых процентов. Проценты с точным числом дней ссуды обычно получаются выше процентов с приближенным числом дней ссуды.

Учетная ставка процента определяется по формуле:

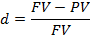
Ставка процента и учетная ставка взаимосвязаны, т.е. зная один показатель можно рассчитать другой.

Вывод формул:

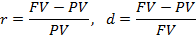
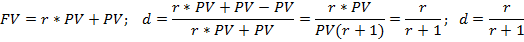
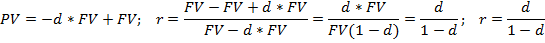
Дисконт фактор показывает какую часть сумма PV составляет в сумме FV.

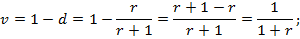
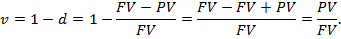
Индекс роста В суммы PV за время t

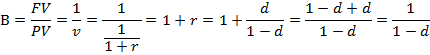
Индекс роста показывает во сколько раз увеличилась первоначальная сумма за время t.

Индекс роста за время t = t₁ + t₂ + t₃ +…+t_n равен:

В=В₁*В₂*В₃*…В_n.

При n=1 FV=PV(1+r),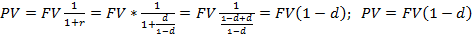

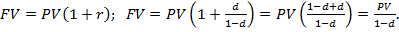
Т.о. FV=PV(1+r), PV=FV(1-d),