Модель доходности финансовых активов (САМР)

Модель САМР описывает зависимость между рыночным риском и требуемой доходностью при определенных условиях (инвесторы ведут себя рационально, измеряют время в одних единицах, мыслят сходным образом, заимствуют и предоставляют средства в долг под безрисковую ставку и др.). При соблюдении указанных допущений инвестиционный портфель, повторяющий пропорции рынка, должен быть оптимальным инвестиционным решением для всех инвесторов. Логика данной модели построена на том, что решение о вложении инвестиций принимается с учетом двух факторов - ожидаемой доходности 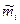и риска, мерой которого является дисперсия или стандартное отклонение доходности. Итоговое уравнение данной модели имеет следующий вид:

, (5.11)

где 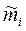- ожидаемый доход на ценную бумагу i при равновесии рынка;

m_f- ставка дохода на безрисковую ценную бумагу (например, гаранти­рованные ценные бумаги с фиксированным доходом в виде государственных облигаций).

b _i - коэффициент акции i – является мерой рыночного риска акции (измеряет изменчивость доходности акции по отношению к доходности среднерыночного портфеля). Он определяет угол наклона характеристической линии акции, построенной по статистическим данным о доходности i-й акции и среднерыночной доходности.

– рыночная премия за риск.

Выражение (5.11) описывает линейную связь между доходом ценной бумаги и ее бета-коэффициентом и его называют уравнением линии рынка ценных бумаг (SML). Графическое изображение линии SML приведено на рис. 5.5.

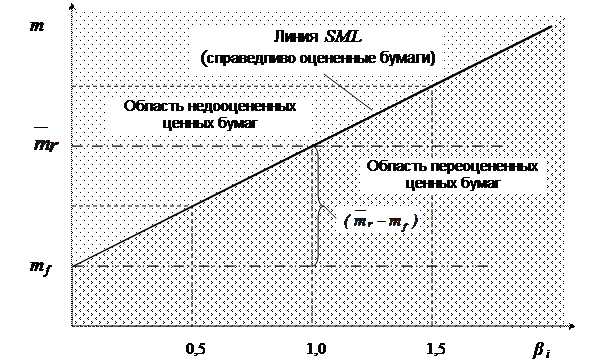
Рис.5.5. Общий вид графика линии рынка ценных бумаг SML

Линия SML отражает идеальную зависимость между β и эффективностью бумаг и портфелей. Все точки, лежащие на прямой SML, соответствуют «справедливо» оцененным бумагам (портфе­лям). Над линией находится область недооцененных ценных бумаг, а под линией – область переоцененных.

Линия рынка ценных (SML) бумаг отражает зависимость риск – доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме m_f, сложенной с произведением премии за рыночный риск 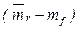и b - коэффициента акции:

Отсутствие риска по безрисковым ценным бумагам влечет за собой и мини­мальный уровень прибыли. В силу этого безрисковые бумаги являются главным регулятором прибылей и рисков.

По данным Э. Димсона (полученным на основе анализа фондовых рынков за 50 лет), в экономически развитых странах мира рыночная премия ( 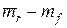) составляет 8% годовых. Например, при ставке безрискового вложения (в долларах) равной 5% годовых и коэффициенте b для некоторой компании равном 0,65, инвестор в условиях устойчивой экономики должен потребовать от акций данной компании долгосрочную доходность в размере:

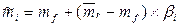= 5% + 8% x 0,65 = 10,2% годовых, долл.

Но на развивающихся рынках (в том числе и фондовый рынок России) подобные оценки могут оказаться неправомерными.

Величины коэффициентов «бета» в модели САРМив рыночной модели сходны по смыслу, но рыночная модель в отличие от САРМ не является моделью равновесия финансового рынка. Кроме того, рыночная модель использует рыночный индекс, который в общем случае не охватывает рыночный портфель, используемый в САРМ.

Существует ряд причин, по которым требуемая и ожидаемая доходности не совпадают: 1) изменение безрисковой ставки ввиду пересмотра ожидаемого темпа инфляции, 2) изменение b, 3) переоценка отношения инвеcтo-pa к риску.

Модель САРМ хорошо обоснована с позиции теории, но она не может быть подтверждена эмпирически, еепараметры с трудом поддаются оценке и поэтому ее применение на практике ограничено.

Для преодоления недостатков САРМ разработаны альтернативные модели риск – доходность. Наиболее перспективной из новых моделей построена на теории арбитражного ценообразования (Arbitrage Pricing Theory, АРТ). основы которой были сформулированы американским экономистом Жераром Дэбре, получившего Нобелевскую премию по экономике за новые подходы к общей теории экономического равновесия.

5.6. Теория арбитражного ценообразования

Известно, что модель САРМ является однофакторной – в ней риск являет­ся функцией одного фактора - b – коэффициента, выражающего зави­симость между доходностью ценной бумаги и доходностью рынка. Арбитражная теория ценообразования учитывает множество факторов, оказывающих влияние на ожидаемую доходность, как по каждому виду ценных бумаг, так и по фондовому рынку в целом. Уравнения арбитражной теории ценообразования строятся на основе следующих предположений:

- финансовые рынки являются совершенными;

- в условиях рыночного равновесия невозможен арбитраж, т.е. такая инвестиционная стратегия, которая обеспечивает положительный доход при нулевых или даже отрицательных чистых инвестициях;

- в условиях равновесия на финансовых рынках доходность отдельных ценных бумаг и фондового рынка в целом описывается линейным многофакторным уравнением, сами эти факторы оконча­тельно определяются в процессе экспериментальных расчетов.

Предпосылка о совершенных финансовых рынках означает, что каждый инвестор может формировать портфель любой структуры из рисковых и безрисковых вложений вследствие делимости финансовых инструментов, их абсолютной ликвидности и возможности реализации «коротких продаж».

Согласно последней предпосылке (наиболее важной) проводить анализ и получать надежные прогнозы доходности рынка и отдельных рисковых финансовых инструментов с помощью моделей арбитражного ценообразования можно только в условиях рыночного равновесия. При отклонении от состояния равновесия на финансовых рынках более важную роль играют спекулятивные факторы, определяющие возможность арбитража.

Арбитражна финансовых рынках означает возможность извлечения дохода за счет разницы цен, т.е. чисто спекулятивных операций.

С учетом этого выделение и анализ многофакторных моделей доходности фондового рынка и отдельных рисковых активов имеют смысл только в состоянии рыночного равновесия при отсутствии возможностей арбитража.

Основное уравнение арбитражной теории ценообразования.Доходность отдельных видов ценных бумаг, как и фондового рынка в целом, описывается следующим уравнением регрессии:

q _j = a _j + b_1j F₁ + b_2j F₂ + ... + b_{m j} F_m + e _j , (5.12)

где q _j – доходность j-й ценной бумаги, j = 1,2,...,п;

F_k - значение k-то фактора, k =1, 2,...,m;

b_kj - коэффициент чувствительности ценной бумаги j к фактору k;

a_j - свободный член уравнения;

e _j - случайная переменная с нулевым математическим ожиданием и отличной от нуля дисперсией, независимая от рассматриваемых факторов, j=1, 2,...,n.

Если из присутствующих на рынке ценных бумаг можно составить портфель, не требующий дополнительных инвестиций, то компоненты его структуры удовлетворяют следующему соотношению

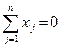, (5.13)

где x_j - доля стоимости j-й ценной бумаги в портфеле инвестора, если x_j > 0, то это означает покупку j-й ценной бумаги, если x_j < 0 - ее продажу.

Считается, что с увеличением числа ценных бумаг в таком портфеле влияние случайных факторов на доходность портфеля стремится к нулю:

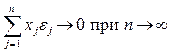(5.14)

т.е. нефакторный риск по портфелю стремится к нулю при увеличении числа ценных бумаг в портфеле.

Предполагается также, что рассматриваемый портфель нечувствителен ни к одному из факторов:

, (5.15)

и имеет нулевой факторный риск. Учитывая, что ожидаемое значение случайной переменной в каждом уравнении (5.12) рав­но нулю и соблюдается условие (5.14), можно показать, что ожидаемая доходность по данному портфелю

.

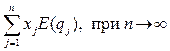Если полученное выражение больше нуля, то это означает, что рассматриваемый портфель является арбитражным, т.е. при нулевых инвестициях имеет место положительная ожидаемая доходность. В условиях рыночного равновесия арбитражные стратегии невозможны и данный портфель будет иметь нулевую ожидаемую доходность:

(5.16)

Если выполняются условия (5.14)–(5.16), то ожидаемая доходность по каждому виду рисковых ценных бумаг может быть представлена в видеосновного уравнения арбитражной теории ценообразования:

E(q _j )= l₀ + l_j b_1j + l_j b_2j + ... + l_{n j} b_{n j} , j = 1,2,...,m. (5.17)

которое должно выполняться для каждой рисковой ценной бумаги, фондового рынка в целом и безрискового актива. Поскольку безрисковая ставка процента не зави­сит от рассматриваемых факторов, то из условия (5.17) следует, что

l₀ = i . (5.18)

Если рассматривать портфели, каждый из которых чувствителен только к одному из выделенных факторов k = 1, 2,...,n, и не чувствителен ко всем остальным, то для каждого такого портфеля уравнение (5.17) превращается в однофакторное, и тогда соответствующий коэффициент l_k можно представить так

l_k = E(q_{p k )} – i , (5.19)

где E(q_pk) - ожидаемая доходность портфеля, чувствительного к k-му фактору и не чувствительного ко всем остальным.

С учетом условий (5.18) и (5.19) уравнение (5.17) можно записать в следующем виде

E(q _j )= i + b_1j (E(q_p1) – i) + b_2j (E(q_p2) – i) + ... + b_{n j} (E(q_pn) – i). (5.20)

Из последнего уравнения следует, что премия за риск по каждой ценной бумаге в форме превышения ожидаемой доходности по бумаге над безрисковой ставкой процента, источником которого является каждый рассматриваемый фактор в отдельно­сти, определяется премией за риск по портфелю, чувствительному только к данному фактору.

Соотношение коэффициентов чувствительности в модели APT и коэффициентов бэта в модели САРМ.У. Шарп отмечал, что между этими коэффициентами существует следующее линейное соотношение для каждого вида рискового актива:

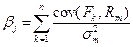(5.21)

где cov(F_k ,R_m) - ковариация между k-м фактором и доходностью рыночного портфеля. При фиксированных значениях первого сомножителя под знаком суммы коэффициент бэта по данному рисковому активу является линейной комбинацией коэффициентов чувствительности по факторам в модели APT.

Учитывая соотношения (5.19), (5.20) и (5.21), коэффициенты в уравнении (5.17) можно представить так

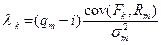(5.22)

причем этот коэффициент может быть положительным или отрицательным в зависимости от знака ковариации доходности рыночного портфеля и соответствующего фактора. Каждый отдельный фактор, учитываемый в модели APT, может содействовать как увеличению, так и уменьшению ожидаемой доходности рассматриваемого актива или портфеля.

Из условий (5.17) и (5.21) следует, что уравнение линии рынка ценных бумаг в модели САРМ и представимо в виде

E(R _j ) = i + ((E(R_m) − i) b _j ,

где E(R_m)- ожидаемая доходность рыночного портфеля, является частным случаем уравнения (5.20) с единственным фактором - доходностью рыночного портфеля и коэффициентом чувствительности b _j = b _{j .}

Основные факторы в моделях арбитражного ценообразования.Главной проблемой модели APT является то, что перечень и экономический смысл факторов, которые учитываются при построении уравнения (5.12), заранее не определяются и должны быть установлены в процессе расчетов. К значимым обычно относятся три – пять факторов:

- основные макроэкономические показатели: валовой внутренний продукт, темп роста объема промышленного производства, темпы роста доходов населения, уровень инфляции и т.п.;

- показатели рынка капитала: темпы роста доходности на биржевой индекс, разница между процентными ставками - краткосрочной и долгосрочной, разность между ставками процента по государственным и корпоративным облигациям (процентный спрэд), по долгосрочным и краткосрочным обязатель­ствам (временной спрэд) и др.;

- прочие экономические показатели, например изменение цен на нефть и другие энергоносители, темпы роста тех или иных государственных расходов и т.п.

Для оценки качества модели APT и устойчивости выделенной группы факторов после окончательного обоснования факторов оцениваются параметры уравнения регрессии второго порядка, где зави­симая переменная - доходность актива или фондового рынка, а независимые - коэффициенты чувствительности и, соответственно, бэта для однофакторной модели, оцененные по различным временным промежуткам. Анализ полученного уравнения и его статистических характеристик позволяет оценить устойчивость полученных соотношений.

Особенности формирования арбитражных портфелей.Арбитраж является одной из возможных стратегий поведения инвестора на рынке, которая включает два направления:

первое, приобретение товаров или ценных бумаг по относительно низкой цене, и продажа их же (в данный период или одновременно) по относительно более дорогой цене позволяет извлекать дополнительный доход за счет разницы на различных рынках;

второе, при обращении на фондовом рынке простых акций с одним и тем же курсом, но разной ожидаемой доходностью, продавая акции с относительно более низкой ожидаемой доходностью и приобретая акции с относительно более высокой ожидаемой доходностью, можно получать дополнительный арбитражный доход в следующем периоде.

Основная особенность арбитража как инвестиционной стратегии состоит в том, что реализация этой стратегии позволяет извлекать доход при нулевых чистых инвестициях, если соответствующий товар или ценная бумага уже находятся в собственности инвестора.

Наличие арбитража на рынке позволяет судить о равновесии рынка и о том, насколько быстро рынок может в это состояние вернуться. Факторные модели используются для прогнозирования доходности фондового рынка и отдельных финансовых инструментов в условиях рыночного равновесия, когда ценные бумаги или портфели с одинаковой чувствительностью к рассматриваемым факторам, имеют одинаковые ожидаемые доходности.

Пример 5.2. Предположим, что в результате оценки параметров некоторого однофакторного уравнения в форме q _i = a _i + b_i F + e _i были установлены следующие данные по трем видам акций (см. табл. 5.3).

Таблица 5.3

Данные по акциям

Акция	Ожидаемая доходность (qi)	Коэффициент чувствительности ( bi )
Акция 1-го вида		0,6
Акция 2-го вида		2,5
Акция 3-го вида		3,4

Необходимо показать возможность формирования арбитражного портфеля из этих акций, который обеспечивал бы положительную ожидаемую доходность при нулевых чистых инвестициях.

Решение

1. Обозначим структуру искомого портфеля через x = (x₁, x ₂, x ₃), где x ₁, x ₂, x ₃ - доли стоимости акций в портфеле первого, второго и третьего вида соответственно, которые могут принимать положительные и отрицательные значения. При положительном значении x _i акции данного вида нужно покупать, при отрицательном - продавать. Причем доход от продажи одних акций должен совпадать с расходами по приобретению других акций, т.е. портфель не требует никаких дополнительных инвестиций. Такой портфель будет арбитражным в том случае, когда он будет иметь положительную ожидаемую доходность.

2. Составим систему уравнений относительно неизвестных компонент структуры арбитражного портфеля в общем виде:

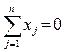- условие того, что портфель составлен из ценных бумаг присутствующих на рынке и не требует дополнительных инвестиций,

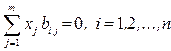- условие нечувствительности портфеля ни к одному фактору (нулевого факторного риска),

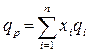- ожидаемая доходность портфеля.

3. Запишем данную систему с учетом исходных условий:

x ₁ + x ₂ + x ₃ = 0;

0,6 x ₁+ 2,5 x ₂ + 3,4 x ₃ = 0;

12 x ₁ + 25 x ₂ + 8 x ₃ = q_p.

4. Решая эту систему в матричном виде в среде Excel, (см. рис. 5.6) для раз-

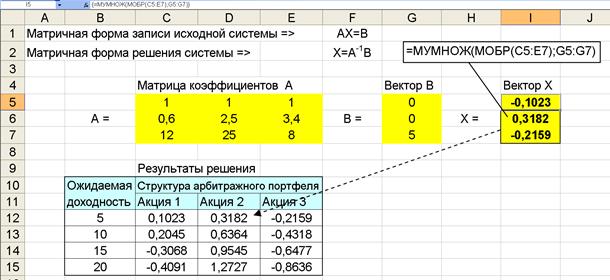
Рис. 5.6. Результаты расчета структуры арбитражного портфеля

личных значений ожидаемой доходности портфеля q_p, получим соответствующие результаты по составу арбитражного портфеля (см. рис. 5.6 или табл. 5.4)

Таблица 5.4

Арбитражный портфель из акций трех видов

Ожидаемая доходность арбитражного портфеля qp, (%)	Структура арбитражного портфеля
Доля акций 1-го вида, x1	Доля акций 2-го вида, x2	Доля акций 3-го вида, x3
	-0,1023	0,3182	-0,2159
	-0,2045	0,6364	-0,4318
	-0,3068	0,9545	-0,6477
	-0.4091	1,2727	-0,8636

Для ожидаемой доходности 5% арбитражная стратегия состоит в том, чтобы продавать акции 1-го и 3-го видов и приобретать на эту же сумму акции 2-го вида. Аналогичные выводы можно сделать и по другим вариантам доходности (10, 15 и 20%).

5. Используя последнее уравнение исходной системы, оценим возможность получения дополнительной доходности в полученном портфеле:

q_p = 12×(- 0,1023) + 25×0,3182 8×(- 0,2159) = 5%.

Если инвестор имел бы портфель из акций указанного вида стоимостью 200 тыс. руб., то он должен продать акции 1-го и 3-го вида на сумму

200 × (0,1023 + 0,2159) = 200 × 0,3182 = 63,64 тыс.руб.

и купить акции 2-го вида на ту же сумму, что позволит увеличить ожидаемую доходность его портфеля на 5%. При этом риск нового портфеля инвестора не изменится, поскольку по условиям формирования арбитражного портфеля его риск относительно мал и близок к нулю.

6. Предположим, что исходный портфель инвестора имел следующую структуру: x = (0,4;0,2;0,4), тогда ожидаемая доходность такого портфеля составит:

q_p = 12 × 0,4 + 25 × 0,2 + 8 × 0,4 = 13%.

Коэффициент чувствительности портфеля к рассматриваемому фактору риска можно определить по второму уравнению исходной системы:

b_р = 0,6 ×0,4 + 2,5 × 0,2 + 3,4 × 0,4 = 2,1.

7. Используя арбитражный портфель, имеющий ожидаемую доходность, равную 5%, можно сформировать новый портфель, который при том же самом уровне чувствительности и риска имеет более высокую ожидаемую доходность 18% (см. табл. 5.5).

Таблица 5.5

Использование арбитражного портфеля

Акция	Исходный портфель	Арбитражный портфель	Cформированный портфель
Акция 1-го вида	0,4000	-0,1023	0,2977
Акция 2го вида	0,2000	0,3182	0,5182
Акция 3о вида	0,4000	-0,2159	0,1841
Коэффициент чувствительности	2,1000	0,0000	2,1000
Ожидаемая доходность, %
Риск, %		близок к нулю	примерно 25

Кроме того, стоимость сформированного портфеля будет равна стоимости исходного. Изменилась только структура портфеля и повысилась его ожидаемая доходность. Таким образом, арбитражные портфели позволяют повышать ожидаемую доходность портфеля инвестора.

Используемая и рекомендуемая литература

Основная

1. Беннинга, Шимон. Финансовое моделирование с использованием Excel.: 2-е издание.: Пер. с англ. – М.: ООО «И.Д. Вильямс», 2007. – 207. – 592 с. : ил.

2. Воронцовский А.В. Управление рисками: Учеб. пособие. 2-е изд., испр. и доп. – СПб.: Изд-во С.Петерб. ун-та, 2000; ОЦЭиМ, 2004. – 458 с.

3. Ступаков В.С., Токаренко Г.С. Риск-менеджмент: Учеб. пособие. – М.: Финансы и статистика, 2007. – 228 с.

4. Уткин Э.А., Фролов Д.А. Управление рисками предприятия: Учеб.-практ. пособие. – М.: ТЕИС , 2003 - 247 с.

5. Финансовая математика: Математическое моделирование финансо­вых операций: Учеб. пособие / Под ред. В.А. Половникова и А.И. Пилипенко. М.: Вузовский учебник, 2004.

6. Чернова Г.В., Кудрявцева А.А. Управление рисками: Учеб. пособие. – М. : Проспект, 2008. – 160 с.

7. Шапкин А.С., Шапкин В.А. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. 7-е изд. – М.: Издательско-торговая корпорация «Дашков и К^о», 2009. – 544 с.

8. Энциклопедия финансового риск-менеджмента / Под ред. канд. экон. наук А.А. Лобанова и А.В.Чугунова. – 4-е изд., испр. и доп. – М.: Альпина Бизнес Букс, 2009. – 932 с.

Дополнительная

1. Бартон Т.Л., Шенкир У.Г., Уокер П.Л. Комплексный подход к риск-менеджменту: стоит ли этим заниматься, издательский дом «Вильямс», 2003.

2. Бригхэм Ю., Эрхардт М. Финансовый менеджмент. 10-е изд. / Пер. с англ. под ред. к.э.н. Е.А. Дорофеева. – СПб.: Питер, 2007. -960с.

3. Воробьев С. Н., Балдин К. В. Управление рисками в предпринимательстве – М.: Издательско-торговая корпорация «Дашков и Ко», 2007. – 772 с.
4. Долматов, А.С. Математические методы риск-менеджмента: учебное пособие / А.С. Долматов. – М.: Издательство «Экзамен», 2007. – 319 с.

5. Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений: Учеб. посбие для вузов. - М: Финансы, ЮНИТИ, 1998. – 400 с.

6. Моделирование рисковых ситуаций в экономике и бизнесе: Учеб. пособие / А.М. Дубров, Б.А. Лагоша, Е.Ю. Хрусталев, Т.П. Барановская; Под ред. Б.А. Лагоши. 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 224 с.

7. Орлова И.В. Экономико-математическое моделирование. Практическое пособие по решению задач. – М.: Вузовский учебник, 2004.

8. Островская Э. Риск инвестиционных проектов / Эльжбета Островская. Пер. с польского. – М: ЗАО «Издательство экономика», 2004. – 269 с.

9. Первозванский А.А., Первозванская Т.Н. Финансовый рынок: расчет и риск. – Инфра-М, 1994. -192 с.

10. Риск-анализ инвестиционного проекта: Учебник для вузов / Под ред. М.В. Грачевой. – М.: ЮНИТИ-ДАНА, 2001. 231 с.

11. Риск-менеджмент инвестиционного проекта: учебник для студентов вузов, обучающихся по экономическим специальностям / Под ред. М.В. Грачевой, А.Б. Секерина. – М.: ЮНИТИ-ДАНА, 2009. – 544с.

12. Тэпман Л.Н. Риски в экономике: Учеб. пособие для вузов / Под ред. проф. В.А. Швандера. – М.: ЮНИТИ-ДАНА, 2002. – 380 с.

13. Шапкин А.С., Шапкин В.А. Теория риска и моделирование рисковых ситуаций. Учебник – М.: Издательско-торговая корпорация «Дашков и К^о», 2009. – 880 с.

14. Хохлов Н.В. Управление риском: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 1999. – 239 с.

Периодические издания

1. Журнал «Управление финансовыми рисками»

2. Журнал «Финансовый менеджмент»

3. Журнал «Менеджмент в России и за рубежом»

4. Журнал «Менеджмент сегодня»