Определение уровня процентной ставки

Понятие «процентные деньги»

Под процентными деньгами или процентами понимают абсолютную величину дохода от предоставления денег в долг в любой из форм:

– Выдача денежной ссуды

– Продажа в кредит

– Помещение денег на сберегательный счет

– Учет векселя

– Покупка сберегательного сертификата, облигаций и т.д.

Какой бы вид не имели проценты, это всегда конкретное проявление экономической категории ссудный процент

Для определения его величины используют договорную процентную ставку, т.е. отношение суммы процентных денег, выплачиваемых за фиксированный отрезок времени, к величине ссуды.

Если ставка измеряется в виде десятичной дроби, то в контракте ее фиксируют с точностью до 1/16 и точнее. В формулах вычисления делают подстановку в долях.

В финансовом количественном анализе процентные ставки применяются не только как инструмент приращения суммы долга, но и в более широком смысле – как измерители степени доходности (эффективности) финансовых операций вне зависимости от того, имел или нет место процесс передачи денежных средств и нарастания суммы долга.

В зависимости от формы осуществления финансовой операции или от условий контракта, используют различные концепции начисления процента – на базе простой и сложной ставок процента, КОТОРЫЕ ОТЛИЧАЮТСЯ ДРУГ ОТ ДРУГА БАЗОЙ ДЛЯ НАЧИСЛЕНИЯ ПРОЦЕНТА.

Простая ставка процента

Если ставка процента применяется к постоянной исходной базе на протяжении всего периода договора, то говорят об использовании простой процентной ставки.

Под наращенной суммой ссуды (долга, депозита и т.д.) понимается ее первоначальная сумма вместе с начисленными на нее процентами к концу срока.

Наращенная сумма определятся умножением первоначальной суммы на множитель наращения, который показывает во сколько раз наращенная сумма больше первоначальной суммы.

Для записи формул используют следующие общепринятые обозначения:

I – проценты за весь срок

P – первоначальная сумма

S – наращенная сумма, т.е. P + I

i – ставка процента

Начисление процентов за один период:

За n периодов: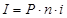

Процесс изменения суммы долга с начисление простых процентов описывается арифметической прогрессией, члены которой:

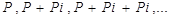
Формула для расчета наращенной суммы по простой процентной ставке имеет вид:

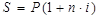
- множитель наращения

*Примечание: выделяют три варианта расчета процентов:

1. точные проценты с точным числом дней ссуды (год – 365 дней, полугодие – 182 дня)
2. обыкновенные проценты с точным числом дней ссуды (банковский способ). Дает несколько больший результат, чем применение точных процентов (год – 360 дней)
3. обыкновенные проценты с приближенным числом дней ссуды. Используют, как правило, для промежуточных вычислений, не требующих абсолютной точности (месяц – 30 дней всегда).

Дифференцирование по простой ставке процента

Финансовый менеджер может столкнуться с задачей, обратной определению наращенной суммы – по заданной сумме S, которую следует уплатить через время n нужно определить сумму полученной ссуды, т.е. P.

Ситуация для такого рода расчетов – разработка условий контракта, удержание процентов сразу при выдаче ссуды и др.

В таких случаях говорят, что сумма S, дисконтируется, а сам процесс начисления и удержания процентов вперед наз. учетом.

Проценты в виде разницы S – P = D, наз. дисконтом

Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины на некоторый момент времени при условии, что в будущем она составим величину S, вне зависимости от того, имела ли место финансовая операция, предусматривающая начисление процента или нет.

Величину P, найденную дисконтированием S, наз.приведенной (P’)

С помощью дисконтирования учитывается фактор времени. Формулу расчета величины P получаем из базовой ф. расчета наращенной суммы:

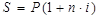, отсюда:

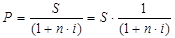(формула математического дисконтирования)

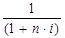- множитель дисконтирования. Показывает, какую долю составляет P в S.

*Примечание: если n ≠ целому числу лет, тогда:

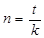
где t – число дней сделки

k – временная база, т.е. число дней в году

Определение продолжительности ссуды:

в годах:

1)

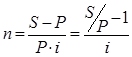
2)

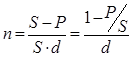
в днях:

3)

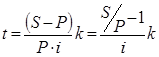
4)

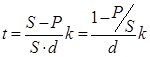
где d – учетная ставка

Сложная процентная ставка

Если проценты не выплачиваются сразу после их начисления, а присоединяются к основной сумме долга, то говорят об использовании концепции сложного процента (когда база для наращения увеличивается с каждым шагом во времени). Начисление и присоединение процента представляет собой наращение.

Присоединение процента к сумме, которая служила базой для их расчета наз. капитализацией процента.

Она может иметь место 1 раз в год, 2, 4, 12/365 и чаще.

Формула для расчета наращенной суммы по сложным процентам имеет вид:

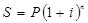
где i – годовая ставка процента

P – первоначальная величина (база)

n – число периодов (лет)

(Проценты капитализируются один раз в год)

Получили данную ф., описывая геометрическую прогрессию:

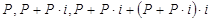или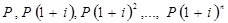

*Примечание:

1. В данной формуле множителем наращения является 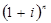- сложный дискурсивный коэффициент
2. Существуют готовые таблицы значений множителя наращения для целых чисел n
3. Если начисляют годовые проценты при дробном числе лет, т.е. n = a + b, где a - целая часть года, b – дробная, то ф. для расчета наращенной суммы кроме возведения сложного дикурсивного коэффициента в дробную степень может иметь вид:

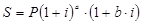
Рассчитанные по разным ф. величины наращенной суммы будут несколько отличаться друг от друга

Финансовая рента и аннуитет

Последовательность денежных поступлений, производимых через равные промежутки времени наз. финансовой рентойили аннуитетом.

Используют следующую классическую формулировку: серия равновеликих платежей с равными интервалами между последовательными платежами в течение определенного времени наз. аннуитетом.

Использование последовательных платежей очень многосторонне. Это может быть оплата по заключенным контрактам, получение или погашение кредита (среднесрочного или долгосрочного), инвестирование денежных средств, создание фондов целевого назначения или финансирование частных пенсионных накопительных программ, безвозвратные и возвратные аннуитеты страховых компаний и т.д.

Параметры, являющиеся характеристиками финансовой ренты:

1. Член ренты – величина каждого отдельно взятого платежа

2. Период ренты – временной интервал между двумя платежами

3. Срок ренты – время от начала реализации ренты до последнего платежа

4. Процентная ставка – ставка, используемая для расчета наращенной суммы ренты или для дисконтирования платежей, составляющих ренту

5. Момент осуществления платежа (в начале, в середине или в конце года)

6. Частота начисления процента – количество периодов в году начисления процентов

7. Наращенная сумма – сумма всех членов потока платежей вместе с начисленными на них процентами на конец срока, т.е. на дату последней выплаты.

Т.о. наращенная сумма аннуитета показывает в какую сумму превратится капитал, вносимый через равные промежутки времени в течение всего срока ренты вместе с начисленными процентами

8. Современная (приведенная) величина или современная величина потока платежей – сумма всех его членов, уменьшенная (дисконтированная) на величину процентной ставки на определенный момент времени, совпадающий с началом потока платежей или предшествующий ему. Т.е. современная величина показывает, какую сумму следовало бы иметь первоначально, чтобы разбив ее на равные взносы, на которые начислялись бы установленные проценты в течение срока ренты, можно было бы обеспечить получение наращенной суммы

9. Коэффициент наращения ренты (коэффициент аккумуляции вкладов) – показывает, во сколько раз наращенная сумма ренты больше первого члена ренты

10. Коэффициент приведения ренты показывает, сколько рентных платежей содержится в современной величине ренты.

11. Вид ренты отличается определенным набором характеристик.

Выделяют следующие виды рент:

Дополнительный классификационный признак	Вид ренты	Примечание
1. Дискретные ренты	Годовые Р-срочные*   Сверхгодичные	Платежи производятся 1 раз в год Платежи производятся несколько раз в год Платежи производятся реже, чем 1 раз в год
2. Непрерывные ренты		Частота платежей очень высока, стремится к непрерывной
3. В зависимости от частоты начисления процентов		С начислением процентов 1 раз в год С начислением процентов несколько раз в год* С непрерывным начислением процентов
4. По условию выплаты	Верная   Условная	Выплата, которая не ограничена какими-либо условиями Выплата, которая обусловлена наступлением какого-либо события
5. В зависимости от стабильности размера платежа	Постоянные   Переменные	Когда платежи, члены ренты равновелики между собой Платежи, члены ренты не равны между собой
6. По количеству членов ренты	Ограниченные   Вечные	Когда ренты имеют фиксированное число членов Когда ренты не имеют конечного числа членов
7. По моменту, с которого начитается реализация рентных платежей	Немедленные   Отложенные (отсроченные)	Платежи производятся сразу же после заключения контракта Указывается определенный период отсрочки
8. По моменту выплат членов ренты	Обычные (постнумеранда) Пренумеранда   Средние	Платежи производятся в конце соответствующих периодов Платежи производятся в начале периода Платежи производятся в середине периода
9. По способу начисления процентов	Сложные Простые
* *	Общая рента	Когда рентные платежи вносятся несколько раз в год, начисление процентов несколько раз в год, но число платежей не совпадает с числом начислений процентов

Понятие «процентные деньги»

Под процентными деньгами или процентами понимают абсолютную величину дохода от предоставления денег в долг в любой из форм:

– Выдача денежной ссуды

– Продажа в кредит

– Помещение денег на сберегательный счет

– Учет векселя

– Покупка сберегательного сертификата, облигаций и т.д.

Какой бы вид не имели проценты, это всегда конкретное проявление экономической категории ссудный процент

Для определения его величины используют договорную процентную ставку, т.е. отношение суммы процентных денег, выплачиваемых за фиксированный отрезок времени, к величине ссуды.

Если ставка измеряется в виде десятичной дроби, то в контракте ее фиксируют с точностью до 1/16 и точнее. В формулах вычисления делают подстановку в долях.

В финансовом количественном анализе процентные ставки применяются не только как инструмент приращения суммы долга, но и в более широком смысле – как измерители степени доходности (эффективности) финансовых операций вне зависимости от того, имел или нет место процесс передачи денежных средств и нарастания суммы долга.

В зависимости от формы осуществления финансовой операции или от условий контракта, используют различные концепции начисления процента – на базе простой и сложной ставок процента, КОТОРЫЕ ОТЛИЧАЮТСЯ ДРУГ ОТ ДРУГА БАЗОЙ ДЛЯ НАЧИСЛЕНИЯ ПРОЦЕНТА.

Простая ставка процента

Если ставка процента применяется к постоянной исходной базе на протяжении всего периода договора, то говорят об использовании простой процентной ставки.

Под наращенной суммой ссуды (долга, депозита и т.д.) понимается ее первоначальная сумма вместе с начисленными на нее процентами к концу срока.

Наращенная сумма определятся умножением первоначальной суммы на множитель наращения, который показывает во сколько раз наращенная сумма больше первоначальной суммы.

Для записи формул используют следующие общепринятые обозначения:

I – проценты за весь срок

P – первоначальная сумма

S – наращенная сумма, т.е. P + I

i – ставка процента

Начисление процентов за один период:

За n периодов: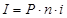

Процесс изменения суммы долга с начисление простых процентов описывается арифметической прогрессией, члены которой:

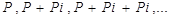
Формула для расчета наращенной суммы по простой процентной ставке имеет вид:

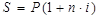
- множитель наращения

*Примечание: выделяют три варианта расчета процентов:

1. точные проценты с точным числом дней ссуды (год – 365 дней, полугодие – 182 дня)
2. обыкновенные проценты с точным числом дней ссуды (банковский способ). Дает несколько больший результат, чем применение точных процентов (год – 360 дней)
3. обыкновенные проценты с приближенным числом дней ссуды. Используют, как правило, для промежуточных вычислений, не требующих абсолютной точности (месяц – 30 дней всегда).

Дифференцирование по простой ставке процента

Финансовый менеджер может столкнуться с задачей, обратной определению наращенной суммы – по заданной сумме S, которую следует уплатить через время n нужно определить сумму полученной ссуды, т.е. P.

Ситуация для такого рода расчетов – разработка условий контракта, удержание процентов сразу при выдаче ссуды и др.

В таких случаях говорят, что сумма S, дисконтируется, а сам процесс начисления и удержания процентов вперед наз. учетом.

Проценты в виде разницы S – P = D, наз. дисконтом

Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины на некоторый момент времени при условии, что в будущем она составим величину S, вне зависимости от того, имела ли место финансовая операция, предусматривающая начисление процента или нет.

Величину P, найденную дисконтированием S, наз.приведенной (P’)

С помощью дисконтирования учитывается фактор времени. Формулу расчета величины P получаем из базовой ф. расчета наращенной суммы:

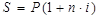, отсюда:

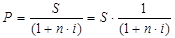(формула математического дисконтирования)

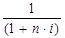- множитель дисконтирования. Показывает, какую долю составляет P в S.

*Примечание: если n ≠ целому числу лет, тогда:

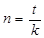
где t – число дней сделки

k – временная база, т.е. число дней в году

Определение продолжительности ссуды:

в годах:

1)

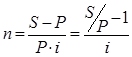
2)

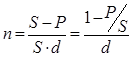
в днях:

3)

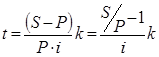
4)

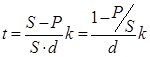
где d – учетная ставка

Определение уровня процентной ставки

Это бывает необходимо при сравнении контрактов по степени доходности в случае, когда проценты в явном виде не указаны. Решив уравнения наращения относительно i и d, получим:

Процентная ставка: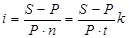

Учетная ставка: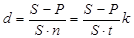

где k – временная база

Формула для расчета наращенной суммы для учетной ставки:

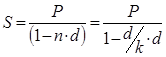
В мировой практике выделяют и такие 2 концепции начисления процентов: