Определение ускорения при координатном способе задания движения
Вектор ускорения точки 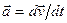 в проекции на оси получаем:
в проекции на оси получаем:
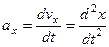 ,
, 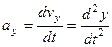 ,
, 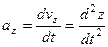
или
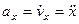 ,
, 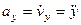 ,
, 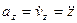 ,
,
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
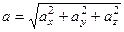 ;
;
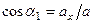 ,
, 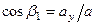 ,
, 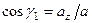 ,
,
где 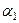 ,
, 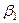 ,
, 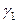 - углы, образуемые вектором ускорения с координатными осями.
- углы, образуемые вектором ускорения с координатными осями.
Пример 3. Движение точки задано уравнениями 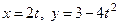 .
.
Из первого уравнения t=x/2. Подставив во второе, получим уравнение траектории: 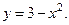
Это уравнение параболы. В начале движения, при t=0, точка находилась на самом верху, в положении M0 ( 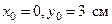 ).
).
А, например, при t =0,5 c она будет в положении M с координатами 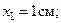
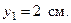
Проекции скорости на оси 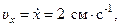
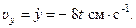
При 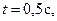
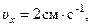
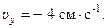
И модуль скорости 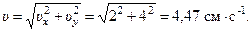
Составляющие скорости по осям и вектор её показаны в масштабе на рис. 7.
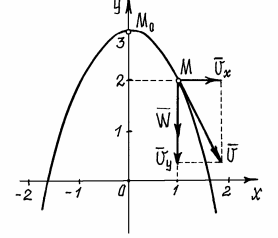
Рис.10
Проекции ускорения ax= 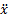 =0, ay=
=0, ay= 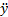 =-8 см∙с-2. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
=-8 см∙с-2. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки
При естественном способе задания движения вектор 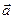 определяют по его проекциям на оси
определяют по его проекциям на оси 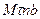 , имеющие начало в точке М и движущиеся вместе с нею (рис.11). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось
, имеющие начало в точке М и движущиеся вместе с нею (рис.11). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось 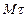 - вдоль касательной к траектории в сторону положительного отсчета расстояния s; ось Mn - по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось
- вдоль касательной к траектории в сторону положительного отсчета расстояния s; ось Mn - по нормали, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось 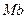 - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль Mn, лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль
- перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль Mn, лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль 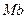 - бинормалью.
- бинормалью.
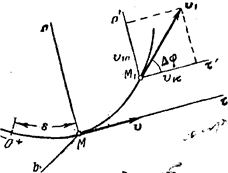
Рис.11
Было показано, что ускорение точки 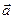 лежит в соприкасающейся плоскости, т.е. в плоскости
лежит в соприкасающейся плоскости, т.е. в плоскости 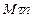 ; следовательно, проекция вектора
; следовательно, проекция вектора 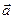 на бинормаль равна нулю (
на бинормаль равна нулю ( 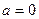 ).
).
Вычислим проекции 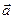 , на две другие оси.
, на две другие оси.
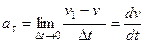 .
.
будем иметь
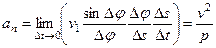 ,
,
Окончательно
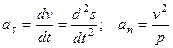 .
.
Итак, проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) s no времени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю (ab=0). Эти результаты выражают собою одну из важных теорем кинематики точки.
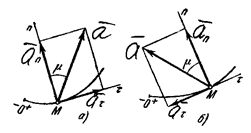
Рис.12
Отложим вдоль касательной 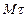 и главной нормали Mn векторы
и главной нормали Mn векторы  и
и 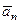 , численно равные
, численно равные 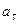 и
и 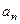 (рис. 12). Эти векторы изображают касательную и нормальную составляющие ускорения точки.При этом составляющая
(рис. 12). Эти векторы изображают касательную и нормальную составляющие ускорения точки.При этом составляющая 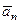 будет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая
будет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая  может быть направлена или в положительном, или в отрицательном направлении оси
может быть направлена или в положительном, или в отрицательном направлении оси 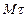 в зависимости от знака проекции
в зависимости от знака проекции 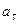 (см. рис.12, а и б).
(см. рис.12, а и б).
Вектор ускорения точки 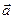 изображается диагональю параллелограмма, построенного на составляющих
изображается диагональю параллелограмма, построенного на составляющих  и
и 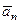 . Так как эти составляющие взаимно перпендикулярны, то по модулю:
. Так как эти составляющие взаимно перпендикулярны, то по модулю:
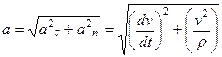 .
.
