Работа в поле тяготения. Потенциал поля тяготения

Рассмотрим, чему равна работа, соверша­емая силами поля тяготения при переме­щении в нем материальной точки мас­сой т. Вычислим, например, какую надо затратить работу для удаления тела мас­сой т от Земли. На расстоя­нии R (рис. 39) на данное тело действует сила

F=GmM/R².

При перемещении этого тела на расстоя­ние dR затрачивается работа

Знак минус появляется потому, что сила и перемещение в данном случае противо­положны по направлению (рис.39).

Если тело перемещать с расстояния R₁

до R₂, то затрачивается работа

Из формулы (25.2) вытекает, что за­траченная работа в поле тяготения не зависит от траектории перемещения, а оп­ределяется лишь начальным и конечным положениями тела, т. е. силы тяготения действительно консервативны, а поле тя­готения является потенциальным (см. § 12).

Согласно формуле (12.2), работа, со­вершаемая консервативными силами, рав­на изменению потенциальной энергии системы, взятому со знаком минус, т. е.

А = -DП = -(П₂-П₁)= П₁-П₂.

Из формулы (25.2) получаем

П₁-П₂= - m(GM/R₁ - GM/R₂).

(25.3)

Так как в формулы входит только раз­ность потенциальных энергий в двух со­стояниях, то для удобства принимают по­тенциальную энергию при R₂®¥ равной нулю ( lim П₂=0 _{при R2®¥}). Тогда (25.3) запишется в виде П₁= - GmM/R₁. Так как пер­вая точка была выбрана произвольно, то

П=-GmM/R.

Величину

j = П/m,

являющуюся энергетической характери­стикой поля тяготения, называют потенци­алом. Потенциал поля тяготения j —ска­лярная величина, определяемая потенци­альной энергией тела единичной массы в данной точке поля или работой по пере­мещению единичной массы, из данной точ­ки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой M, равен

j=-GM/R, (25.4)

где R — расстояние от этого тела до рас­сматриваемой точки.

Из формулы (25.4) вытекает, что гео­метрическое место точек с одинаковым потенциалом образует сферическую повер­хность (R = const). Такие поверхности, для которых потенциал постоянен, назы­ваются эквипотенциальными.

Рассмотрим взаимосвязь между потен­циалом поля тяготения (j) и его напря­женностью (g). Из выражений (25.1) и (25.4) следует, что элементарная работа dA, совершаемая силами поля при малом перемещении тела массой т, равна

dA=-тdj.

С другой стороны, dA=Fdl (dl—эле­ментарное перемещение). Учитывая (24.1), получим, что

dA=mgdl,

т. е.

mgdl=-mdj,

или

g=-dj/dl.

Величина dj/dl характеризует изменение потенциала на единицу длины в направле­нии перемещения в поле тяготения. Можно показать, что

g=-.gradj, (25.5)

где gradj=(dj/дx)i+(дj/dy)j+(дj/dz)k—

градиент скаляра j (см. (12.5)). Знак минус в формуле (25.5) указывает, что вектор напряженности g направлен в сто­рону убывания потенциала.

В качестве частного примера, исходя из представлений теории тяготения, рас­смотрим потенциальную энергию тела, на­ходящегося на высоте h относительно Земли:

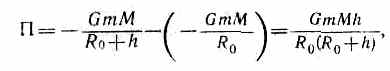
где R₀— радиус Земли.

Так как

P=GmM/R²₀и g=P/m=GM/R²₀,

(25.6) то, учитывая условие h<<R₀, получим

П=mGMh/R²₀= mgh.

Таким образом, мы вывели формулу, со­впадающую с (12.7), которая постулиро­валась раньше.

Космические скорости

Для запуска ракет в космическое про­странство надо в зависимости от постав­ленных целей сообщать им определенные начальные скорости, называемые космиче­скими.

Первой космической(или круговой) скоростьюv₁называют такую минималь­ную скорость, которую надо сообщить те­лу, чтобы оно могло двигаться вокруг Зем­ли по круговой орбите, т. е. превратиться в искусственный спутник Земли. На спут­ник, движущийся по круговой орбите ра­диусом r, действует сила тяготения Зем­ли, сообщающая ему нормальное ускоре­ние v²₁/r. По второму закону Ньютона,

GmM/r²=mv²₁/r.

Если спутник движется недалеко от поверхности Земли, тогда r»R₀ (радиус Земли) и g=GM/R²₀(cм. (25.6)), поэтому у поверхности Земли

Первой космической скорости недоста­точно для того, чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость называется второй кос­мической. Второй космической(или пара­болической) скоростьюv₂ называют ту наименьшую скорость, которую надо со­общить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спут­ник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической. Для того чтобы тело (при отсутствии со­противления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кине­тическая энергия была равна работе, совершаемой против сил тяготения:

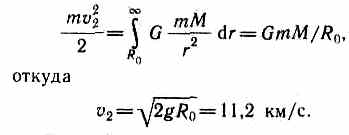
Третьей космической скоростьюv₃на­зывают скорость, которую необходимо со­общить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца. Третья космическая скорость v₃=16,7 км/с. Сообщение телам таких больших начальных скоростей явля­ется сложной технической задачей. Ее первое теоретическое осуществление на­чато К. Э. Циолковским, им была выведе­на уже рассмотренная нами формула (10.3), позволяющая рассчитывать ско­рость ракет.

Впервые космические скорости были достигнуты в СССР: первая — при за­пуске первого искусственного спутника Земли в 1957 г., вторая — при запуске ра­кеты в 1959 г. После исторического полета Ю. А. Гагарина в 1961 г. начинается бур­ное развитие как советской, так и зару­бежной космонавтики.