Вирівнювання теодолітних ходів

Результати вимірювання кутів та ліній обтяжені похибками. Вирівнювання ходів полягає в визначені допустимих нев’язок кутових та лінійних вимірювань, введення поправок в результати вимірів та обчислення координат точок теодолітних ходів.

При вирівнюванні замкнених та розімкнених теодолітних ходів (рис. 8.11, а,б) обчислюють:

1. Практичну суму виміряних кутів по ходу або полігону

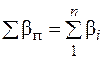, (8.1)

де b_і – виміряні кути на точках, ліві – 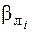, або праві – .

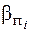2. Теоретичну суму:

- внутрішніх кутів замкнених полігонів

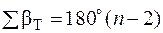; (8.2)

- лівих кутів розімкнених ходів

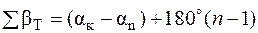, (8.3)

- правих кутів розімкнених полігонів

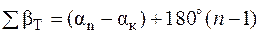, (8.4)

де п – кількість вершин хода (полігона);

a_п, a_к – дирекційний кут початкової та кінцевої вихідної сторони (рис. 8.11, а,б для замкненого полігона a_к = a_п);

b_л, b_п – ліві або праві по ходу виміряні кути.

3. Обчислюють кутову нев’язку f_b та допустиму кутову нев’язку за формулами

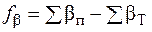; (8.5)

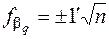. (8.6)

Коли 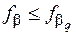, то вирівнювання продовжують. Якщо ця вимога не дотримується, то перевіряють попередні обчислення і при необхідності виконують повторне вимірювання горизонтальних кутів.

4. Обчислюють поправки в кути 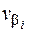та виправлені значення кутів 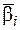за формулами:

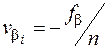; (8.7)

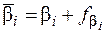. (8.8)

Контроль 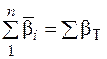. (8.9)

5. Обчислюють дирекційні кути сторін ходу за формулами:

a_і+1 = a_і +b_л ± 180^о, (8.10)

або a_і+1 = a_і - b_п ± 180^о. (8.11)

Контроль: Обчислене a_к повинно дорівнювати дирекційному куту вихідної кінцевої лінії a_к.

6. Обчислюють прирости координат за формулами

Dх_і = d_i × cosa_і, або Dх_і = d_i × cosr_і ; (8.12)

Dу_і = d_i × sina_і або Dу_і = d_i × sinr_і , (8.13)

де r_i – румб лінії (розділ 2 §8)

d_і – горизонтальні прокладання ліній.

7. Обчислюють нев’язки приростів координат за формулами:

- для замкнених полігонів

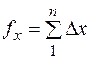; (8.14)

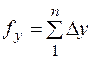, (8.15)

- для розімкнених полігонів

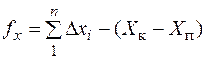; (8.16)

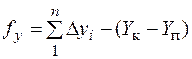, (8.17)

де Х_п, Х_к; Y_п, Y_к – координати початкового та кінцевого вихідних пунктів опорної геодезичної мережі.

8. Виконують контроль лінійних вимірювань:

- обчислюють абсолютну величину лінійної нев’язки

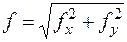, (8.18)

- обчислюють відносну лінійну похибку

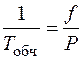, (8.19)

де Р – довжина (периметр) ходу або полігону

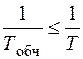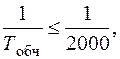Контроль: якщо , або (8.20)

де 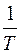– задана відносна точність лінійних вимірів, то обчислення продовжують. В противному разі перевіряють попередні обчислення або повторно вимірюють лінії теодолітного ходу.

9. Обчислюють поправки до приростів координат u_Dx, u_Dy та їх виправлені значення 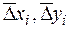за формулами:

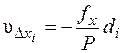; (8.21)

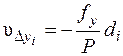, (8.22)

та 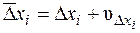; (8.23)

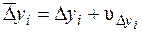. (8.24)

Контроль: 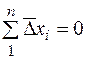та 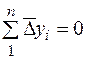– для замкненого полігону,

та 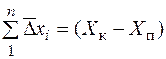; 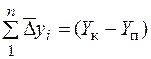– для розімкненого полігону.

10. Обчислюють координати точок полігону за формулами

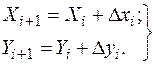. (8.25)

Приклад математичної обробки теодолітного ходу наведено в таблиці 8.1.

Таблиця 8.1

Відомість розрахунку координат

Точка полігона	Виміря- ний кут bлів	Виправ лений кут bвипр	Дирек- ційний кут, a	Румб, r	Горизонтальна проекція ліній, d, м	Розрахований приріст	Виправлений приріст	Координата точки
Dх	Dу	Dх	Dу	х, м	у, м
	25²		246о18¢00²
	97о12¢30²	97о12¢55²				+9	+4			+659,98	+1067,82
	25²		163о30¢55²	16о29¢05²	198,23	-190,09	56,21	-199,00	+56,25
	89о15¢30²	89о15¢55²				+7	+3			+469,98	+1124,07
	25²		72о46¢50²	72о46¢50²	162,34	+48,03	+155,06	+48,10	+155,09
	198о57¢30²	198о57¢55²				+9	+5			+518,08	+1279,16
	25²		91о44¢45²	88о15¢15²	203,021	-6,10	+202,93	-6,01	+202,98
	179о58¢30²	179о58¢55²				+9	+4			+512,07	+1482,14
	25²		91о43¢40²	88о16¢20²	199,97	-6,04	+199,88	-5,95	+99,92
	164о59¢00²	164о59¢25²				+11	+6			+506,12	+1682,06
	25²		76о43¢05²	76о43¢05²	235,01	+54,00	+228,76	+54,11	+228,82
	199о17¢30²	199о17¢55²								+560,23	+1910,88
			96о01¢00²
Sb =	929о40¢30²				Р = 998,77	-100,20	+842,84	-99,77	+843,26

f_b = Sb_лів – (a_к - a_п) – n × 180^o;

f_b = 929^о40¢30² - (96^о01¢ - 246^о18¢ + 1080^о) = - 2¢30²;

;

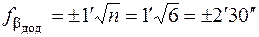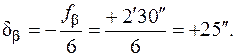
f_x = SDx – (x_n – x₀) = - 100,20 – (560,23 – 659,98) = - 0,45 м;

f_у = SDу – (у_n – у₀) = +842,84 – (1910,88 – 1067,82) = - 0,22 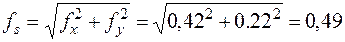м;

м;

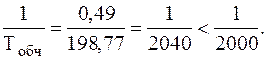
При використанні електронних тахеометрів вирівнювання ходів виконується автоматично за допомогою їх програмного забезпечення.