Теорема о трех перпендикулярах
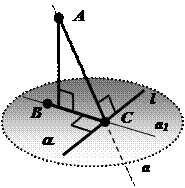Теорема: Для того чтобы прямая, принадлежащая плоскости, была перпендикулярна наклонной к этой плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной.
Необходимое условие:
Дано: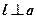 
Доказать: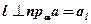 
Доказательство:
; 
; 
;
; 
; 
;
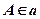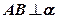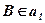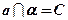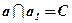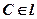Через точки А, В, С проходит единственная плоскость АВС. По признаку перпендикулярности прямой и плоскости прямая l перпендикулярна плоскости АВС:
1) 
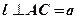по условию теоремы;
2) 
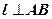, так как 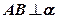, а значит, она перпендикулярна любой прямой, принадлежащей плоскости 
.
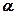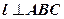, значит, прямая l перпендикулярна любой прямой, принадлежащей плоскости 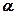. Следовательно, 
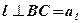, т. е. .
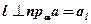Достаточное условие:
Дано: 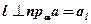Доказать: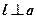
Доказательство:
По признаку перпендикулярности прямой и плоскости прямая l перпендикулярна плоскости АВС:
1. 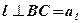по условию теоремы;
2. 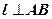, так как 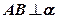, а значит, перпендикулярна любой прямой, принадлежащей плоскости .
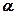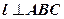, значит, прямая l перпендикулярна любой прямой, принадлежащей плоскости 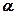. Следовательно, 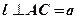, т. е. .
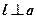Вывод: Чтобы доказать, что наклонная перпендикулярна прямой, лежащей в плоскости, надо показать, что её проекция перпендикулярна этой прямой.
Упражнения:
Из точки О, удаленной от плоскости a на 12 см, проведена к этой плоскости наклонная АВ, равная 37 см. Найти проекцию наклонной АВ на плоскость a .
2. Из точки вне плоскости проведена к этой плоскости наклонная, равная 20 см, образующая с этой плоскостью угол 45°. Найти расстояние от данной точки до плоскости.
Из центра круга радиуса 18 см восстановлен перпендикуляр к его плоскости. Найти расстояния от конца этого перпендикуляра до точек окружности, если длина перпендикуляра 80 см.
Из центра О круга радиуса 3 дм восстановлен перпендикуляр ОВ к его плоскости. К окружности проведена касательная в точке А и на этой касательной отложен от точки касания отрезок АС, равный 2 дм. Найти длину наклонной ВС, если длина перпендикуляра ОВ равна 6 дм.
5. Из вершины D прямоугольника АВСD, стороны которого АВ = 9 см и ВС = 8 см, восстановлен к плоскости прямоугольника перпендикуляр DF = 12 см. Найти расстояния от точки F до вершин прямоугольника.
8. ДВУГРАННЫЙ УГОЛ. ЛИНЕЙНЫЙ УГОЛ ДВУГРАННОГО УГЛА
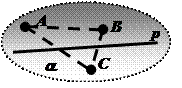III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
Множества, на которые прямая р разбивает множество не принадлежащих ей точек плоскости a , называются открытыми полуплоскостями с границей р.