Обратного распространения ошибки

Один из вариантов решения этой проблемы – разработка наборов выходных сигналов, соответствующих входным, для каж­дого слоя НС, что, конечно, является очень трудоем­кой операцией и не всегда осуществимо. Второй вариант – дина­мическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изме­няются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный метод, несмотря на кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант – распространение сигналов ошибки от выходов НС к ее входам, в на­правлении, обратном прямому распространению сигналов в обыч­ном режиме работы. Этот алгоритм обучения получил название процедуры обратного распространения ошибки [163]. Алгоритм обратного распространения ошибки – это итера­тивный градиентный алгоритм обучения, который используется с целью минимизации среднеквадратичного отклонения текущих от требуемых выходов многослойных НС с последова­тельными связями. Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:

(1)

где 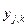– реальное выходное состояние j-го нейрона выходного слоя НС при подаче на ее входы k-го образа; – требуе­мое выходное состояние этого нейрона.

Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация методом градиентного спуска обеспечивает подстройку весовых коэффици­ентов следующим образом:

(2)

где w_ij - весовой коэффициент синаптической связи, соединяющей i-й нейрон слоя (q-1) с j-м нейроном слоя q; h - коэффициент ско­рости обучения, 0 <h <1.

В соответствии с правилом дифференцирования сложной функции:

, (3)

где s_j – взвешенная сумма входных сигналов нейрона j, т. е. аргу­мент активационной функции. Так как производная активационной функции должна быть определена на всей оси абсцисс, то функ­ция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых НС. В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой (см. табл. 2 прошлой лекции). Например, в случае гиперболического тангенса:

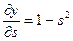. (4)

Третий множитель 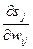равен выходу нейрона предыдущего слоя y_i^(q-1).

Что касается первого множителя в (3), он легко расклады­вается следующим образом:

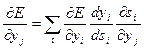(5)

Здесь суммирование по i выполняется среди нейронов слоя (q+1).

Введя новую переменную:

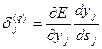(6)

получим рекурсивную формулу для расчетов величин d_j^(q) слоя q из величин d_j^(q+1) более старшего слоя (q+1):

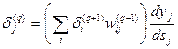(7)

Для выходного слоя:

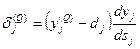(8)

Теперь можно записать (2) в раскрытом виде:

(9)

Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (9) дополняется значением из­менения веса на предыдущей итерации:

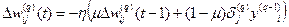, (10)

где m - коэффициент инерционности; t – номер текущей итерации.

Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится сле­дующим образом:

Шаг 1. Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигна­лы распространяются от входов к выходам, рассчитать значения

, (11)

где n_q-1– число нейронов в слое (q-1), вход нейрона j слоя q.

Шаг 2. Рассчитать 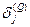для выходного слоя по формуле (7). Рассчитать по формуле (8) изменения весов 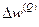для слоя Q.

Шаг 3. Рассчитать по формулам (8) и (9) и 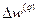для всех остальных слоев, q=Q-1, … , 1.

Шаг 4. Скорректировать все веса в НС:

. (12)

Шаг 5. Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.

Рассмотренный алгоритм обратного распространения ошиб­ки подразумевает наличие некоего внешнего звена, предостав­ляющего НС, кроме входных, целевые выходные об­разы. Алгоритмы, основанные на подобной концепции, называются алгоритмами обучения с учителем. Для их успешного функциони­рования необходимо наличие экспертов, задающих на предвари­тельном этапе для каждого входного образа эталонный выходной.