О геометрических соотношениях саженей
Анализируя функции саженей, Б.А. Рыбаков отмечает следующие особенности их применения [4]:
- возможности измерения одного и того же объекта разными видами саженей;
- «одновременное пользование разными мерами длины объясняется заложенными в этих мерах при их создании строгими геометрическими соотношениями» (т.е. теория Эвклида прослеживается — А. Ч.);
- графическое построение по двум системам мер длины (по простой и мерной саженям) древних схем — «вавилонов» (система вписанных квадратов), предназначенных, по-видимому, для восстановления пропорций утраченных саженей и служивших одновременно символом зодческой мудрости (рис. 1).
Останавливаясь на сопряженности древнерусских саженей, Б.А. Рыбаков показывает, что если ее представить как квадрат со стороной, равной длине прямой сажени 152,7 см, то косая сажень окажется диагональю этого квадрата: 216= 152,7 х √2 .
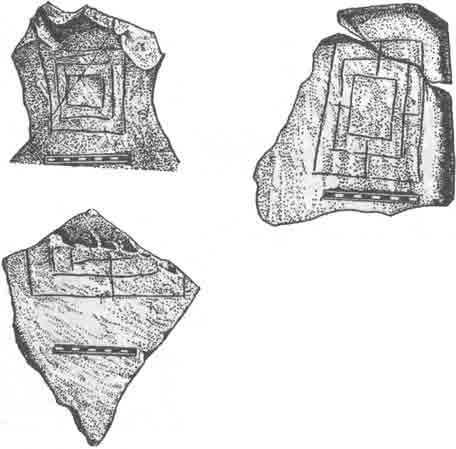
Рис. 1. "Вавилоны" [4]
То же соотношение просматривается между мерной (176,4 см) и великой (249,46 см) саженями:
249,46 = 176,4 √2, где √2 = 1,41421... - иррациональное число.
Исходя из этой пропорциональности Б.А. Рыбаков строит "вавилон", восстанавливающий остальные сажени (рис. 2) по системе вписанных и описанных размеров саженей.
В дополнение можно показать, что квадрат, построенный на окружности, описывающей "вавилон" Б.А. Рыбакова, будет иметь своей стороной сажень косую (рис.2). Отмечу также, что у всех "вавилонов", найденных в археологических раскопках, отсутствуют диагонали, без которых восстановление мерных инструментов невозможно. А это свидетельствует о том, что знание пропорций саженей относилось к сокровенному знанию, которое мастера передавали ученикам и не допускали его выхода за пределы гильдии посвященных.
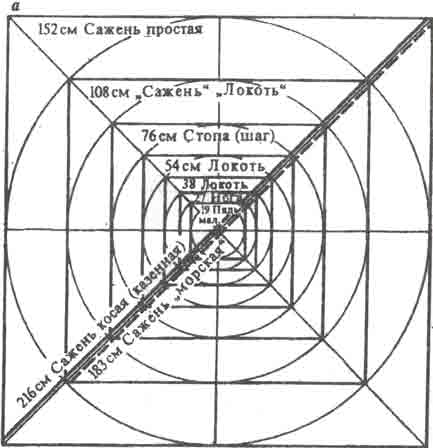
Рис. 2. "Вавилон" русской меры [4]
Продолжая изучение свойств "вавилонов", Б.А. Рыбаков нашел следующие закономерности, определяющие соотношения между саженями (рис. 3). Если возьмем половину длины наиболее распространенной мерной сажени 176,4/2=88,2=А, то следующие зависимости обусловливают нахождение совокупности всех, кроме трубной, саженей: = 249,46 см
| А √3 = 88,2 х 1,73205 | = 152,76см | - простая (прямая) сажень; |
| А √4 = 88,2 х 2,00 | = 176,4 см | - маховая, мерная сажень; |
| А √5 = 88,2 х 2,23607 | = 197,21 см | - "сажень без чети" (царская); |
| А √6 = 88,2 х 2,44995 | = 216,04 см | - косая (казенная) сажень; |
| А √8 = 88,2 х 2,82843 | = 249,46 см | - великая сажень. |
Здесь пропущена зависимость А√7 = 88,2 х 2,64575 = 233,4 см - сажень греческая, которая также не содержится в таблице 1, но часто встречается при обмерах древних сооружений, а позже будет представлена в системе А.А. Пилецкого.
Все операции, предлагаемые Б.А. Рыбаковым, очень хорошо описывают найденную им структуру получения длин саженей и имеют три существенных недостатка:
- не соотносятся между собой по золотому сечению (Б.А. Рыбаков отмечает, а далее будет показано, что соотношение между ними близко золотому числу Ф.);
- древние зодчие не знали сантиметров и миллиметров и, более того, не имели представления о дробях и корнях (деление чисел и дроби до XV в. было известно только ученым математикам), а потому математическими методами для восстановления саженей пользоваться не могли;
- метод не объясняет, почему возникла необходимость в использовании при замере объектов нескольких длин-саженей.
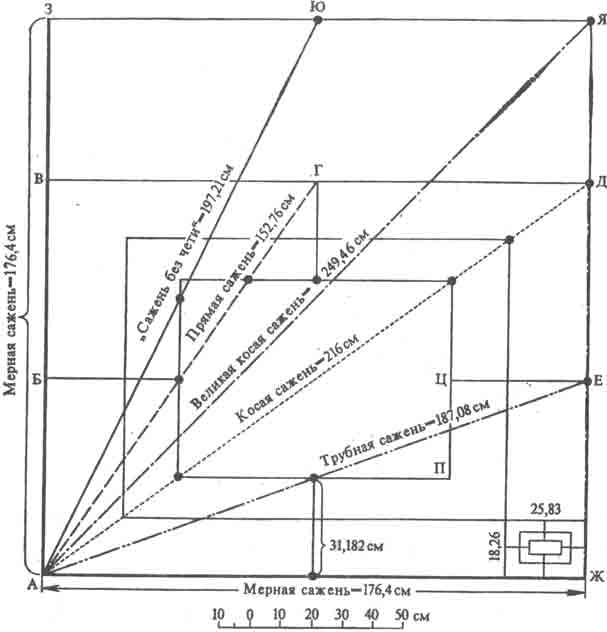
Рис. 3. Геометрическая система древнеруссских саженей [4]
Поскольку метод "вавилонов", как свидетельствуют находки, применялся древними мастерами для пропорционирования саженей по некоторым эталонам, то естественно, что они пользовались им без знания дробей и извлечения корня. Не исключено, однако, что они использовали способы восстановления размеров по любой сохранившейся сажени и даже при отсутствии эталона - по любому прутку с размером, близким к пропорции, человека, например построением треугольных фигур.
Этот метод можно назвать методом "наугольников" (наугольник - плотницкий инструмент треугольной формы [5]). Он заключается в следующем (рис 4): допустим, что эталонная сажень не сохранилась и ее требуется восстановить. Тогда берется деревянный пруток длиной, допустим, в рост плотника. Возьмем для примера рост плотника 172 см, что почти соответствует мерной (маховой) сажени, и примем его за базисную длину. Если три прутка данной длины сложить равнобедренным наугольником, то высота в нем будет равна 148,96 см, что по структуре соответствует сажени простой, да и по длине близко к ней. Если к центру мерной сажени под прямым углом приставить другую мерную сажень и соединить их свободные концы длинными прутками, то получим равносторонний наугольник, длинные стороны которого равны 192,30 см, а это аналог "сажени без чети". Возьмем две полученные простые сажени, соединим их концы под прямым углом и, соединив свободные концы длинным прутком, получим расстояние, равное 210,66 см - аналог сажени косой. Если такую же операцию проведем мерными саженями, получим длину 243,24 см - по назначению аналог сажени великой. И последняя сажень - трубная. Последняя получается, когда к центру косой сажени под прямым углом приставляется сажень простая. При соединении их свободных концов получают равносторонний наугольник, две стороны которого будут иметь длину 182,44 см, что как раз и является аналогом длины трубной сажени.
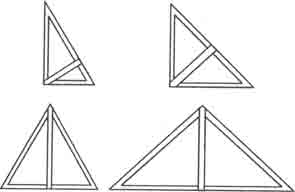
Рис. 4. Наугольники
Восстановление основных саженей закончено. И только морская сажень (в существовании которой как самостоятельного измерительного инструмента сомневается и Б. А. Рыбаков) не восстановлена. Длины всех полученных саженей отличаются от Длин, приведенных в таблице 1, строго на один и тот же коэффициент 1,0255. А это означает, что восстановленные длины саженей с очень высокой точностью сохраняют между собой пропорциональность. Последнее свидетельствует о том, что главное для древних зодчих заключалось не в сохранении эталонной длины отдельных саженей (вот основная причина появления множества типоразмеров саженей, имеющих различную длину), а в соблюдении строгой пропорциональности между ними. Но какова численная величина этой пропорциональности, почему длины саженей выражаются иррациональными числами и зачем надо пользоваться при замерах разными саженями? Данные методы ответа на эти вопросы не дают.
Надо отметить, что Б.А. Рыбаков сам нашел соизмеримость саженей методом квадратов и треугольников, но, по-видимому, не допускал возможности восстановления соизмеримости по прутку любого размера, поскольку предполагал единственное назначение саженей - служить инструментом для измерения длин.
И еще одно. Наиболее точно размеры одного из рисунков "вавилона" были определены на глиняной плите, найденной в старой Рязани на уровне пола в западном притворе Борисоглебовского собора, построенного в середине XII в. ("вавилон" изображен в правом нижнем углу рис. 3). "Вавилон" имел в длину 25,83 см, а в ширину 18,26 см. То есть длина как бы определялась произведением:
18,26 х √2 = 25,82 см.
Но размеры эти древние зодчий получали без привлечения иррациональных чисел и сантиметровых измерений:
длина "вавилона" равна полпяди (пясти) косой сажени (13,5 см) плюс пясть "сажени без чети" (12,32 см):
13,5 + 12,32 = 25,82 см;
ширина - пясть косой (13,5 см) плюс вершок простой (4,774 см):
13,5 + 4,774 = 18,27 см.
Древние зодчий строили объекты и геометрию фигур только саженями на полную длину или целыми частями саженей, что и подтверждается структурой внешних размеров "вавилона". Тем же способом построен и его срединный прямоугольник, имеющий длину, 18,27 см, а ширину 12,91 см. Данная ширина складывается из вершка косой сажени 6,75 см плюс вершок "сажени без чети" (6,16 см):
6,75 + 6,16 = 12,91 см.
Поскольку Б.А. Рыбаков не использовал вершков в своих построениях, он эти взаимосвязи у рязанского "вавилона" не обнаружил. Но на новгородском мериле он обнаружил очень интересные взаимосвязи в структуре применяемых саженей и возможности их использования для производства работ, связанных круглыми конструкциями объектов. А теперь сделаем небольшое отступление и познакомимся с очень необычным и интересным соизмерительным инструментом.
В 1970 г. при раскопках в Новгороде, недалеко от церкви Параскевы Пятницы (год постройки 1207, семьсот девяносто лет назад) в слоях начала XIII в. были найдены обломки деревянного мерила с тремя шкалами крупных и мелких делений, построенных в десятичной системе [6]. Мерило представляло собой два обломка четырехгранного елового бруска размером 28 x 36 мм общей длиной 54 см.
Следует отметить, что найденный облом мерила вызвал большой интерес у специалистов потому, что это был первый древний инструмент с системой трех шкал, все деления которого имели различную длину и целое число раз укладывались в некоторых саженях. К тому же структура деления трех его шкал не соответствовала принятой на Руси системе пропорционирования, на шкалах сохранившегося облома отсутствовали какие либо цифры или знаки, а потому становилась неясной и методика применения мерила.
Тем не менее Б.А.Рыбаков и И.Ш.Шевелев, опираясь на свои представления о методологии применения древних саженей, находят различные способы использования мерила в древнем зодчестве.
Три грани бруска размечены длинными и короткими зарубками (рис. 5), относящимися к разным мерам. Сохранившиеся размеры таковы:
| a - | 4 деления первой шкалы | = 33,4 см; |
| 1 деление в среднем | = 8,35 см; | |
| в - | 6 делений второй шкалы | = 43,9 см; 1 деление = 7,31 см; |
| с - | 3 деления третьей | = 17,8 см; 1 деление = 5,93 см. |
Содержание на одном мериле трех разных шкал, по мнению Б.А. Рыбакова, свидетельствует о том, что оно является расчетным архитектурным инструментом, и каждая шкала, по-видимому, пропорциональна какому-то измерительному инструменту (рис. 5).
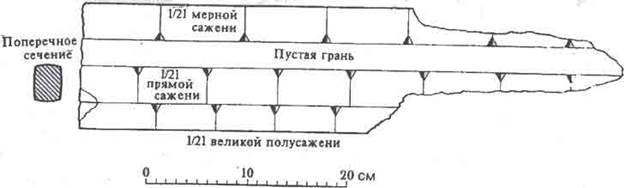
Рис. 5. Облом новгородского мерила [6]
Как уже упоминалось, Б. А. Рыбаков определяет 7 видов саженей, имевших хождение на Руси, и считает достаточным для всех архитектурных операций зодческий минимум в три сажени. Этого числа саженей, по го мнению, хватает для проведения всех измерений, поскольку главное назначение нескольких саженей заключается в облегчении зодчему выполнения многочисленных работ, связанных с различными видами расчетов элементов конструкций, и их совмещения в одном объекте (рис. 6).

Рис. 6. Реконструкция мерила (176,4 см) [6]
Исходя из этих соображений он восстанавливает новгородское мерило в виде стержня, содержащего элементы набора частей длин трех саженей: мерной (маховой), великой (косой) и прямой (простой), но в необычном для древнерусских пропорций делении - каждая сажень делится на 21 элемент (рис. 6). Согласно Б.А. Рыбакову, это необычное деление дает древнему зодчему возможность оперировать элементами каждой сажени для воспроизводства архитектурных деталей и сооружений кругового очертания. Поскольку при любом диаметре круга, когда диаметр делится на 21 часть, в самом круге с большой точностью будут укладываться 66 таких же отрезков. Это деление известно с древности как отношение Архимеда в виде пропорции 22:7 = 3,1428, что и обусловливает возможность построения любой окружности с точностью до 0,05% и проведения операции перевода окружности и отрезка любой окружности (дуги) в линейные меры.
Вернемся к нашим саженям. Познакомимся с другим подходом к изучению структуры этих инструментов, который предлагает архитектор А.А. Пилецкий, Прежде чем рассмотреть его метод, ознакомимся с элементами золотых пропорций, обеспечивающих архитектурным сооружениям оптимальные соразмерности.
