Построение сети с числом нейронов, равным числу обучающих примеров
В [1, 2] рассматриваемый подход называется созданием сети с нулевой ошибкой, что строго говоря, не является точным. Для создания сети используется функция
net = newrbe(Р,Т,SPREAD),
где Р — массив входных векторов, Т — массив целей,SPREAD — "параметр влияния" [1], влияющий на ширину радиальных базисных функций (SPREAD — англ. протяжение).
Функция newrbe создает столько нейронов радиального базисного слоя, сколько имеется входных векторов в массиве Р, и устанавливает веса первого слоя равными Р'(т. е. равными транспонированному массиву Р). При этом смещения устанавливаются равными 0.8326/SPREAD. Это означает, что уровень перекрытия радиальных базисных функций равен 0.5 и все входы в диапазоне ±SPREAD считаются значимыми. Чем больший диапазон входных значений должен быть принят во внимание, тем большее значение параметра влияния SPREAD должно быть установлено.
Веса второго слоя IW{2,1}и смещения b{2}могут быть найдены путем формирования выходов первого слоя A{1}и последующего решения системы линейных алгебраических уравнений (СЛАУ)
[W{2,1} b{2}] * [A{1}; ones] = T
Эта запись означает, что матрица, строки которой представляют искомые векторы весов второго слоя (смещение второго слоя формально представляет собой вес, на который подается единичный входной сигнал), умножается на матрицу, столбцы которой представляют смоделированные выходы первого слоя, а последний столбец единичен. Это произведение принимается равным матрице целевых векторов.
Математически представленная запись представляет собой следующее. Зафиксировано число нейронов первого слоя, центры и ширина. На вход сети подаются обучающие векторы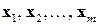 
. При подаче вектор 
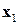выход сети должен быть равен значению 
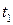целевого вектора и т. д. Тогда веса второго слоя можно определить из решения системы линейных алгебраических уравнений
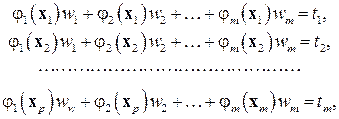
где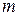 
– число нейронов первого слоя.
В матричной форме систему запишем в виде
,
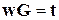где
,
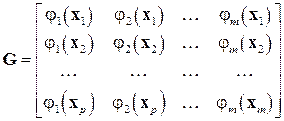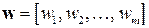– вектор‑строка искомых весов, 
.
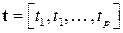Для решения данной системы можно использовать решатель MATLAB, минимизирующий сумму квадратов ошибок
Wb = T/[P; ones(1,Q)]
Обратите внимание, что в данном случае используется решатель "прямой слеш", так как искомые векторы‑строки умножаются на известную матрицу.
Рассмотрим пример [2] использования функции newrbe для построения сети аппроксимирующей функцию, заданную 21 значением аргумента (входами)
>> P = -1:.1:1;
и соответствующими значениями функции (выходами)
>> T = [-.9602 -.5770 -.0729 .3771 .6405 .6600 .4609 ...
.1336 -.2013 -.4344 -.5000 -.3930 -.1647 .0988 ...
.3072 .3960 .3449 .1816 -.0312 -.2189 -.3201];
Построим график обучающего множества (рис. 4.4):
>> plot(P,T,'*r','LineWidth', 2)
>> grid on
>> xlabel('Входной вектор P');
>> ylabel('Целевой вектор T');
>> hold on
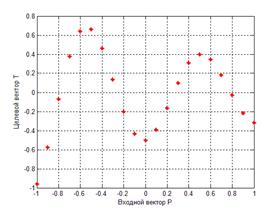
Рис. 4.4. Обучающее множество
Создадим сеть с помощью функции newrbe:
>> net = newrbe(P,T);
Warning: Rank deficient, rank = 13, tol = 2.2386e-014.
> In newrbe>designrbe at 137
In newrbe>create_network at 121
In newrbe at 63
Предупреждение Warning: Rank deficient означает, что решаемая система линейных алгебраических уравнений имеет неполный ранг, равный 13. Значит, в матрице системы из 21 столбца линейно независимыми являются только 13 столбцов, достигнута точность tol=2.2386e-014.
Промоделируем работу сети на векторах из обучающего множества:
>> V = net(P);
Построим график результатов моделирования сети (рис. 4.5)
>> plot(P,V,'ob','MarkerSize',12)
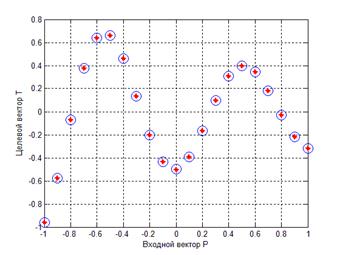
Рис. 4.5. Результаты моделирования работы сети
На обучающем множестве сеть практически идеально аппроксимирует функцию. Но известно [3], что радиальная базисная сеть может обладать плохой обобщающей способностью. В частности, плохой обобщающей способностью может обладать сеть, построенная с помощью функции newrbe. Рассмотрим элементарный пример. Аппроксимируем функцию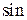 
на 7 примерах:
>> P1=0:pi/3:2*pi;
>> T1=sin(P1);
>> net1 = newrbe(P1,T1);
Построим график:
>> plot(P1,T1,'*r','LineWidth', 2)
>> grid on
>> xlabel('Входной вектор P1');
>> ylabel('Целевой вектор T1');
>> hold on
Промоделируем работу сети на векторах из обучающего множества:
>> V1 = net1(P1);
Построим график результатов моделирования сети (рис. 4.6)
>> plot(P1,V1,'ob','MarkerSize',12)
>> hold on
Результат, как следовало ожидать, отличный (рис. 4.6).
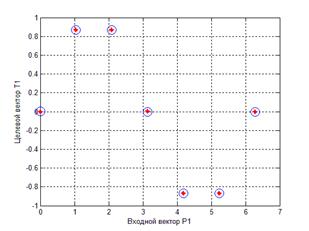
Рис. 4.6. Результаты моделирования работы сети на обучающем множестве
Теперь промоделируем работу сети на 25 примерах:
>> P2=0:pi/12:2*pi;
>> T2=sin(P2);
>> plot(P2,T2)
>> hold on
>> V2 = net1(P2);
>> plot(P2,V2,'+','MarkerSize',6)
Результат на примерах, которые не использовались при построении сети, заметно отличается от целевого значения (рис. 4.7)
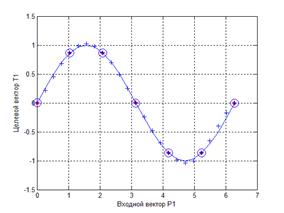
Рис. 4.7. Результаты моделирования работы сети на множестве из 25 примеров (крестообразный маркер)