Расчет зубчатой передачи. В условиях индивидуального и мелкосерийного производства
В условиях индивидуального и мелкосерийного производства, предусмотренного техническим заданием на курсовую работу, в мало- и средненагруженных передачах, а также в открытых передачах применяют стальные зубчатые колеса с твердостью 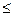 350НВ. При этом обеспечивается нарезание зубьев после термообработки, высокая точность изготовления и хорошая прирабатываемость зубьев.
350НВ. При этом обеспечивается нарезание зубьев после термообработки, высокая точность изготовления и хорошая прирабатываемость зубьев.
Для увеличения нагрузочной способности передачи, уменьшения ее габаритов твердость шестерни HB1 назначается больше твердости колеса HB2,
HB1= HB2+(20-50). (2.1)
Рекомендуемый выбор материалов, термообработки и твердости колес приводятся в таблице 3.6 , а механические свойства сталей в таблице 3.1.
2.5.1. Выбор материалов для изготовления зубчатых колес
Так как мощность привода меньше 10 кВт, то по рекомендации 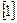 выбираем для изготовления зубчатых колес редуктора стальные зубчатые колеса с твердостью
выбираем для изготовления зубчатых колес редуктора стальные зубчатые колеса с твердостью 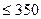 НВ (НВ
НВ (НВ 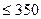 ). Принимаем материал: для колеса - сталь 40X, термообработка – улучшение, твердость сердцевины - 235HВ, твердость на поверхности - 261 НВ.
). Принимаем материал: для колеса - сталь 40X, термообработка – улучшение, твердость сердцевины - 235HВ, твердость на поверхности - 261 НВ.
НВcр=(235+261)/2=248.
Для шестерни - сталь 40X, термообработка – улучшение, твердость сердцевины - 268HВ, твердость на поверхности - 302 НВ.
НВcр=(268+302)/2=285.
HB1=285>HB2= 248 на 37 единиц , т.е. условие (2.1) выполняется.
2.5.2 Определяем допускаемые контактные напряжения [σ]Н и допускаемые напряжения изгиба [σ]F
По таблице 3.6 определяем величину допускаемых контактных напряжений [σ]Н в зависимости от твердости:
[σ]H0=1,8НВcр+67Н/мм2.. (2.2)
Учитывая, что срок службы привода 8 лет, принимаем коэффициент долговечности КHL = 1, тогда получаем:
[σ] Н1 = КHL . [σ]H01ср +67 = 1. 1, 8 . 285+67 = 580 МПа;
[σ] Н2 = КHL . [σ]H02 ср +67 = 1. 1, 8 . 248+67 = 514 МПа.
В качестве расчетных допускаемы напряжений принимаем:
[ 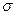 ]H=0.45( [
]H=0.45( [ 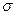 ]H1+[
]H1+[ 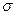 ]H2 ; (2.3)
]H2 ; (2.3)
[ 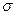 ]H=0.45(580+514)=493 Н/мм2.
]H=0.45(580+514)=493 Н/мм2.
Определяем допускаемое напряжение изгиба по таблице 6[2] в
зависимости от НВср
[ 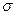 ]F 0=1.03HBср. (2.4)
]F 0=1.03HBср. (2.4)
Учитывая, что срок службы привода 8 лет, принимаем коэффициент
долговечности КFL= 1, тогда
[ 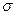 ]F1= КFL 1,03HBср1 = 1∙1,03∙ 285=294 Н/мм2;
]F1= КFL 1,03HBср1 = 1∙1,03∙ 285=294 Н/мм2;
[ 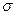 ]F2= КFL1,03 HBср2 = 1∙1,03 ∙248= 256 Н/мм2.
]F2= КFL1,03 HBср2 = 1∙1,03 ∙248= 256 Н/мм2.
2.5.3 Определяем межосевое расстояние редуктора
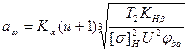 , (2.5)
, (2.5)
где К 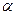 =430 - вспомогательный коэффициент для косозубой передачи;
=430 - вспомогательный коэффициент для косозубой передачи;
КНβ - коэффициент неравномерности нагрузки по длине зуба, принимается по таблице 4.1 в зависимости от коэффициента Ψbd ;
Ψbd - коэффициент ширины колеса относительно делительной окружности шестерни, его значение принимается по таблице 4.2;
Ψвα = 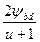 - коэффициент ширины колеса относительно межосевого
- коэффициент ширины колеса относительно межосевого
расстояния.
При симметричности расположения шестерни относительно опор
Ψbd = 0,8…1,4, принимаем Ψbd = 1, тогда Ψbα = 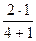 = 0,4 .
= 0,4 .
Согласно значению Ψbd =1, при симметричном расположении колес и
НВ 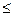 350 по таблице 4.1 принимаем значение
350 по таблице 4.1 принимаем значение
КНβ = 1,04, тогда
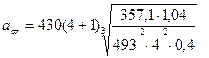 =130 мм.
=130 мм.
Полученное значение округляем до ближайшего значения ГОСТ 6636-69 по таблице 4.3 и окончательно принимаем 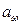 = 130 мм.
= 130 мм.
2.5.4 Определяем нормальный модуль зацепления
mn= (  )
)  =
= 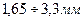 .
. 
По таблице 4.4 принимаем mn=2мм.
2.5.5 Определяем число зубьев шестерни z1, приняв 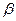 = 10 0, cos
= 10 0, cos 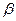 = 0,98,
= 0,98,
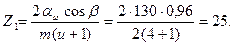
Принимаем z1=32, тогда 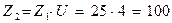 .
.
2.5.6 Уточняем передаточное число:
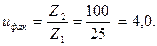
2.5.7 Уточняем фактический угол наклона зубьев:
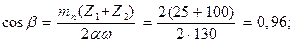
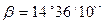 .
.
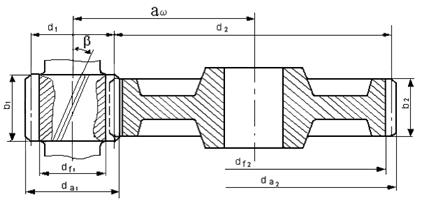
Рисунок 2.1 – Геометрические параметры зубчатого зацеплени
2.5.8 Определяем геометрические параметры шестерни и колеса:
делительный диаметр:
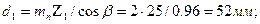
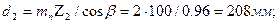
диаметр окружности вершин зубьев:
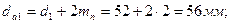
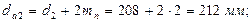
диаметр окружности впадин зубьев:
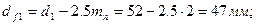
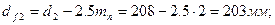
ширина венца колеса:
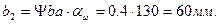
Принимаем 70мм
ширина венца шестерни:
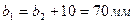 .
.
Уточняем межосевое расстояние:
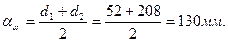
Данные сводим в таблицу геометрических параметров передачи.
Таблица 2.2- Геометрические параметры зубчатого зацепления
| Параметр | Шестерня | Колесо |
Межосевое расстояние, 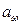 , мм , мм | ||
| Модуль зацепления, mn, мм | ||
| Угол наклона зубьев, β, град | 1403611011 | 1403611011 |
| Число зубьев, z | ||
| Делительный диаметр, d мм | ||
| Диаметр вершин зубьев, dа мм | ||
| Диаметр впадин зубьев, df мм | ||
| Ширина венца, b, мм |
2.5.9 Определяем окружную скорость колес:
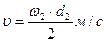 ; d2 - в мм,
; d2 - в мм, 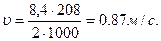
для данной скорости по таблице 4.5 назначаем 8 степень точности изготовления зубчатых колес.
2.5.10 Определение силовых параметров зацепления
 |  |  |
На рисунке 2.2 изображена схема сил в зацеплении цилиндрической косозубой передачи.
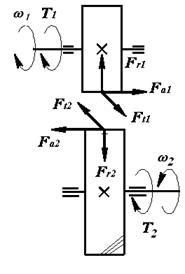
Рисунок 2.2 - Схема сил в зацеплении цилиндрической косозубой передачи
В зацеплении косозубых цилиндрических колес действуют силы:
окружная Ft = 2Т1 /d1 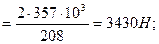
радиальная Fr=Ft × tga / cosb = 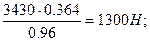 (2.5)
(2.5)
осевая Fa = Ft × tgb=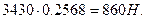
где b - угол наклона зубьев колес.
У зубчатых передач a =200, 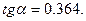
 |
2.5.11 Проверочный расчет передачи по контактным напряжениям, σн.
Определяем контактные напряжения по формуле:
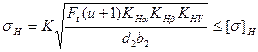 , (2.6)
, (2.6)
где К - вспомогательный коэффициент. Для косозубых передач К= 376; 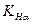 =1,22 - коэффициент, учитывающий неравномерность распределения
=1,22 - коэффициент, учитывающий неравномерность распределения
нагрузки между зубьями (таблица 4.6);
КНβ =1,04 - коэффициент, учитывающий неравномерность распределения
нагрузки по длине контактной линии зуба (таблица 4.1);
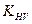 =1,02 - коэффициент, учитывающий влияние динамической нагрузки
=1,02 - коэффициент, учитывающий влияние динамической нагрузки
(таблица 4.7).
Подставив числовые значения коэффициентов в формулу (2.6), получим:
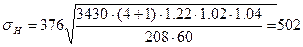 МПа;
МПа;
 <
< 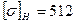 МПа;
МПа;
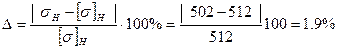 .
.
Недогрузка в пределах допустимой.
2.5.12. Проверочный расчет передачи по напряжениям изгиба, σF.
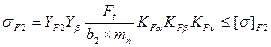 , (2.7)
, (2.7)
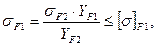 (2.8)
(2.8)
где КFa=0,9 - коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями (таблица 4.6);
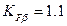 - коэффициент, учитывающий неравномерность распределения
- коэффициент, учитывающий неравномерность распределения
нагрузки по длине контактной линии зуба (таблица 4.1);
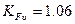 - коэффициент, учитывающий влияние динамической нагрузки
- коэффициент, учитывающий влияние динамической нагрузки
(таблица 4.7);
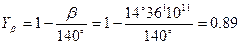 - коэффициент, учитывающий влияние угла
- коэффициент, учитывающий влияние угла
наклона зуба;
YF - коэффициент формы зуба принимается по эквивалентному числу
зубьев
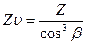 , (2.9)
, (2.9)
для шестерни 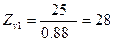 , принимаем zν1 =28;
, принимаем zν1 =28;
для колеса 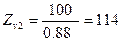 , принимаем zν2 =114.
, принимаем zν2 =114.
По таблице 4.8 находим значения: YF1=3.81, YF2=3.6.
Подставив числовые данные в формулы (2.7) и (2.8), получим;
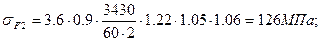

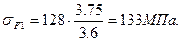
Условия (2.7) и (2.8) выполняются.
Результаты проверочного расчета целесообразно представить в виде таблицы.
Таблица 2.4. – Параметры проверочного расчета закрытой передачи.
| Параметр | Расчетные значения | Допускаемые значения | Примечания | |
| Контактные напряжения, σн, Н/мм2 | Недогрузка 2% | |||
| Напряжения изгиба, σF,Н/мм2 | σF1 | Условие прочности выполняется | ||
| σF2 |
Заключение:результаты проверочных расчетов по контактным напряжениям и напряжениям изгиба показывают, что полученные геометрические параметры редуктора удовлетворяют заданным.
