Расчет сжатых стержней на устойчивость
Как правило, основная проблема при расчете сжатых стержней состоит в том, чтобы сжимающие напряжения s не превышали бы критических значений по устойчивости sКР , т.е.
 . (7.17)
. (7.17)
При продольном изгибе центрально сжатый стержень теряет несущую способность, когда напряжения в его поперечных сечениях достигают критических значений. Поэтому необходимо ввести в расчет коэффициент запаса устойчивости n по отношению к критическим напряжениям, с помощью которого и определяется допускаемое напряжение при расчете на устойчивость:
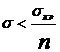 .
.
При расчете же стержней на растяжение применяют условие s < R, где R - расчетное сопротивление на растяжение.
Для унификации расчетов на растяжение и сжатие введем соотношение правых частей двух последних неравенств:
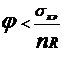 , (7.18)
, (7.18)
откуда 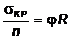 . И тогда (7.17) можно записать так: s < jR.
. И тогда (7.17) можно записать так: s < jR.
Величина j носит название коэффициента уменьшения расчетного сопротивления при расчете на сжатие и является функцией от гибкости стержня l
- Понятие о действии динамических и поворотно-переменных нагрузок.
В инженерной практике же часто встречаются случаи когда нагрузка достаточно быстро изменяет свое направление или величину. Такое нагружение называется динамическим и вызывает значительные силы инерции в сооружении, которые приводят к появлению дополнительных (к статическим) напряжений и деформаций.
Известны случаи, когда инженерные конструкции, рассчитанные с большим запасом прочности на статическую нагрузку, разрушались под действием сравнительно небольших динамических сил.
При изучении динамики упругих систем последние принято классифицировать, прежде всего, по числу их степеней свободы. Под числом степеней свободы понимается число независимых координат, определяющих положение материальных точек системы в произвольный момент времени.
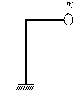 Рис. 8.1 Рис. 8.1 |
Так для системы, изображенной на рис. 8.1, если пренебречь массой стержней, положение сосредоточенной массы m в плоскости чертежа полностью будет определяться двумя независимыми координатами - линейными перемещениями в вертикальном и горизонтальном направлениях. То есть рассматриваемая система будет иметь две степени свободы. Заметим что, так как во всех реальных системах масса конструкции распределена по их объему, поэтому любая произвольно взятая точка является материальной. Следовательно, для определения положения системы в произвольный момент времени, строго говоря, необходимо знать перемещения всех точек рассматриваемой системы. Откуда следует, что все реальные системы в точной постановке задачи, имеют бесконечное число степеней свободы, так как число материальных точек, принадлежащей любой реальной системы, равно бесконечности.
При исследовании колебаний упругих систем различают собственные (свободные) и вынужденные колебания. Под собственными колебаниями понимается движение системы при отсутствии внешних воздействий. Если колебание системы сопровождается действием внешних сил, то движение называется вынужденным.
Промежуток времени за который совершается полный цикл колебаний, носит название периода собственных или вынужденных колебаний, смотря по тому, о каких колебаниях идет речь. Период колебаний обозначается через Т. Величина обратная Т, называется частотой колебаний:
- Определение статики сооружений, задачи, требования, предъявляемые к сооружениям.
Условимся сооружением {системой) называть совокупность твердых тел (элементов), неподвижно соединенных между собой. К любому сооружению предъявляются следующие главнейшие требования:
1. Неподвижность относительно основания и неизменяемость приданной геометрической формы в течение всего срока службы.
2. Прочность, жесткость, устойчивость. Прочность и устойчивость гарантируют безопасность эксплуатации сооружения, а достаточная жесткость ограничивает деформацию его в таких пределах, которые не препятствуют нормальным условиям эксплуатации.
3. Экономичность. Экономичность сооружений определяется наименьшими затратами средств на материалы и возведение сооружения.
Чтобы удовлетворить этим требованиям, надо уметь рассчитывать сооружение. Наука, изучающая расчет сооружений на прочность, жесткость и устойчивость независимо от метода расчета, свойств материала (линейно- или нелинейно-упругий, неупругий) и действующей нагрузки (временной или постоянной, сплошной или сосредоточенной, статической или динамической) называется строительной механикой. Строительная механика широко использует методы расчета и математический аппарат сопротивления материалов, теории упругости и теории пластичности в той мере, в какой они содержат материал для расчета сооружений.
Статикой сооружений называется раздел строительной механики, изучающий методы расчета сооружений на прочность, жесткость и. устойчивость при статическом действии нагрузки, В этой книге рассматриваются только линейно деформируемые сооружения (в дальнейшем— упругие), т. е. такие, для которых в известных пределах нагружения справедлив закон прямо пропорциональной зависимости между силами (нагрузками) и вызываемыми ими перемещениями (закон Гука).
Между статикой сооружений, теоретической механикой и сопротивлением материалов существует тесная взаимосвязь. Сопротивление материалов базируется на знании теоретической механики и изучает методы расчета отдельных элементов сооружений на прочность, жесткость и устойчивость. Статика сооружений применяет - методы теоретической механики и сопротивления материалов к статическому расчету сооружений и служит базой для изучения последующих инженерно-строительных дисциплин.
Основными задачами статики сооружений являются следующие.
1. Установление законов образования наивыгоднейших форм сооружений, т. е. таких форм, которые удовлетворяют вышеизложенным главнейшим требованиям, предъявляемым к сооружениям.
2. Определение внутренних сил в различных сечениях элементов сооружений и выполнение расчетов по подбору и проверке их размеров. Однако в статике сооружений, как правило, эти расчеты самостоятельно не рассматриваются; предполагается, что они известны из курса «Сопротивление материалов».
3. Изучение упругих перемещений, возникающих в сооружении под влиянием внешних воздействии.
4. Исследование устойчивости сооружений. Необходимо отметить, что статика сооружений — наука прикладная, она изучает современные методы расчета сооружений и способствует более экономному расходованию материалов и финансовых ресурсов страны.
Основные допущения, вводимые в статику сооружений для расчета упругих систем, те же, что и в сопротивлении материалов, с той лишь разницей, что они относятся не к отдельному элементу, а ко всему сооружению в целом. 1. В известных пределах нагружения материал сооружения обладает совершенной упругостью, г. е. после прекращения действия нагрузки деформация полностью исчезает.
2. Перемещения точек сооружения, обусловленные его упругими деформациями, весьма малы по сравнению с размерами самого сооружения. Из этого допущения следует, что изменения в расположении сил, происходящие при деформации сооружения, не следует учитывать при составлении уравнений равновесия (при определении реакций связей), а также при определении внутренних сил. Это положение иногда называют принципом начальных размеров.
3. Перемещения точек упругодеформируемого сооружения в известных пределах нагружения прямо пропорциональны силам, вызывающим эти перемещения.
4. Справедлив принцип независимости действия сил: результат действия на сооружение группы сил не зависит от последовательности нагружения ими сооружения и равен сумме результатов действия каждой из сил в отдельности.
Под результатом действия сил в зависимости от конкретной задачи могут пониматься перемещения той или иной точки сооружения, величина внутренней силы и т. п.
- Классификация сооружений.
Основной и наиболее специфической составной частью всех разновидностей схем с сооружениями почвенной очистки сточных вод являются собственно сооружения почвенной очистки, на которых происходит заключительный этап биологической очистки. В связи с этим название всей схемы очистки или очистной станции происходит от названия ее составной части. Специфическим сооружением в схеме с площадками подземного орошения являются сами площадки, поэтому вся система получила название: схема очистки с площадками подземного орошения. Другие элементы схемы очистки (отстойники, дозирующие и распределительные устройства) не являются специфическими, так как водят в состав других разновидностей очистных станций.
Все сооружения почвенной очистки по производительности разделяют на местные, малые, поселковые, городские и районные, расчетные производительности которых составляют соответственно 0,5—25, 25— 700, 1400—10 000, 17 000—80 000 и 100 000—280000 м3/сут (табл. 16).
Городские и районные очистные станции размещаются вне населенного пункта и принимают более 10000 м3 сточных вод в сутки. В качестве очистных канализационных сооружений, рассчитанных на такую производительность, используют, кроме аэротенков, биофильтров и биологических прудов, наземные поля орошения и фильтрации.
Под поселковыми и малыми канализационными очистными сооружениями следует понимать сооружения, размещенные вне пределов небольшого населенного пункта или отдельно стоящего объекта (больничный городок, группа санаториев и т. д.) и принимающие в сутки от 25 до 10000 м3 сточных вод. В качестве очистных канализационных сооружений, рассчитанных на такую производительность, наряду с такими сооружениями, как циркуляционно-окислительные каналы (ЦОК), аэроокислители радиального типа (APT), компактные установки (КУ-200, 400; КУО-25, 75, 400; БИО-50 и 100), биофильтры, применяют малые наземные поля орошения и фильтрации, а также поля подземного орошения.
Под местными канализационными сооружениями следует подразумевать сооружения, размещенные на территории объекта канализования и принимающие до 25 м3 сточных вод в сутки. В качестве местных очистных сооружений» кроме малых биофильтров и компактных установок КУ-12 и БИО-25, применяют сооружения почвенной очистки. Из сооружений почвенной очистки чаще всего устраивают площадки подземного орошения (фильтрации), фильтрующие колодцы, песчано-гравийные фильтры, фильтрующие траншеи с естественным н искусственным сдоем грунта и площадки подпочвенного (внутригрядового) орошения,
В настоящее время различают два вида наземных полей орошения; коммунальные (КПО) и земледельческие (ЗПО), Коммунальные поля орошения устраиваются главным образом для биологической очистки сточных вод. Сельскохозяйственное использование здесь носит второстепенное и вспомогательное значение. Эксплуатацию коммунальных полей орошения осуществляют органы Министерства коммунального хозяйства. Земледельческие поля орошения — ирригационная система, создаваемая с целью, как очистки сточных вод, так и повышения урожайности сельскохозяйственных культур. Эксплуатацию этих сооружений почвенной очистки осуществляют учреждения и ведомства Министерства сельского хозяйства.Таким образом, между КПО и ЗПО существуют различия в целях, размерах и ведомственной подчиненности, а также в качестве и судьбе фильтрата. Однако в связи с тем, что на КПО производится выращивание сельскохозяйственной продукции, к ним должны применяться т. кие же требования, как и к ЗПО.
- Понятие о ферме и ее элементы. Классификация ферм.
Основные понятия о ферме
Конструкции, состоящие из соединенных между собой прямолинейных элементов или стержней, работающих только на растяжение или сжатие, называются фермами (рис 37 и 38).
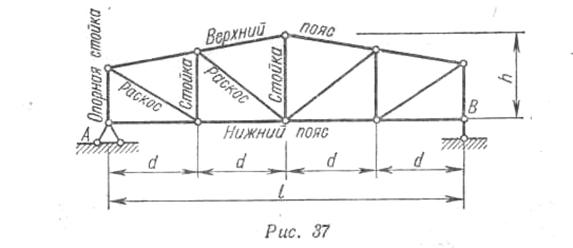
Ферма, изображенная на рис. 37, называется балочной, а на рис. 38 — навесной или консольной.
Расстояние между опорами у первой из них или расстояние от опор до свободного конца у второй обозначается буквой l и называется пролетомфермы; h — высота фермы.
Если оси стержней лежат в одной плоскости, то ферма называется плоской.
Точки, в которых сходятся оси двух или нескольких стержней, называются узлами фермы. Те узлы, которыми ферма опирается на основание, называются опорными (А и В на рис. 37 и 38).
Стержни плоской фермы, расположенные по ее верхнему контуру, называются верхним поясом, расположенные по нижнему контуру — нижним поясом. Растояние между узлами пояса фермы, к которому приложена нагрузка, называется панелью фермы. Ферма, представленная на рис. 37,— четырехпанельная. Внутренние стержни образуют решетку фермы: вертикальные внутренние стержни называются стойками, наклонные—диагоналями или раскосами.

- Методы определения усилий в стержнях.
Замечания к расчету ферм
Замечание 1. Если в ненагруженном узле фермы сходится три стержня, из которых два направлены по одной прямой (рис. 39), то усилие в третьем, так называемом одиночном, стержне равно нулю, а усилия в стержнях, лежащих на одной прямой, равны между собой.
Доказательство. Предположим, что S3 ≠ 0. Тогда равнодействующая усилий S2 и S3, направленная по диагонали параллелограмма, построенного на этих силах, не будет совпадать по направлению с усилием S1 и с ним не уравновесится; следовательно, предположение наше неверно, т. е. S3 = 0.

Замечание 2. Если в узле фермы сходятся два стержня и направление внешней силы, действующей на узел, совпадает с направлением одного из этих стержней (рис. 40), то усилие в этом стержне равно внешней силе и направлено в противоположную ей сторону; усилие же во втором стержне равно нулю, так как по отношению к первому стержню и к силе второй стержень является одиночным.
Замечание 3. Если в узле фермы сходятся три стержня, из которых два направлены по одной прямой, и внешняя сила, приложенная
к узлу, действует по направлению третьего стержня (рис. 41), то усилие в этом стержне равно по величине и противоположно по направлению внешней силе, а усилия в стержнях, лежащих на одной прямой, равны между собой по абсолютной величине, но направлены в противоположные стороны.
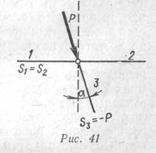
Доказательство. Проектируя силы на направление, перпендикулярное направлению стержней 1 и 2 (рис. 41), получаем Р cos а + S3 cos а = 0, откуда S3 = — Р; из суммы проекций на направление, перпендикулярное стержню 3 и направлению силы Р, получим S1 = S2.
 Замечание 4. Если в узле фермы сходятся под углом два стержня и никаких внешних сил не приложено, то усилия в обоих стержнях равны нулю (рис. 42), так как две силы могут уравновеситься только тогда, когда они направлены по одной прямой; стержни 1 и 2 направлены под углом, они могут уравновеситься лишь в том случае, когда усилие в каждом из них будет равно нулю. Эти четыре замечания полезно помнить, приступая к расчету фермы.
Замечание 4. Если в узле фермы сходятся под углом два стержня и никаких внешних сил не приложено, то усилия в обоих стержнях равны нулю (рис. 42), так как две силы могут уравновеситься только тогда, когда они направлены по одной прямой; стержни 1 и 2 направлены под углом, они могут уравновеситься лишь в том случае, когда усилие в каждом из них будет равно нулю. Эти четыре замечания полезно помнить, приступая к расчету фермы.
Усилия в элементах фермы можно определять, как увидим ниже, различными способами, но в настоящей главе мы воспользуемся методом вырезания узлов, причем задачу будем решать аналитически. В дальнейшем при решении задач будем пользоваться называемым принципом независимости действия сил. Сущность этого принципа состоит в том, что при изучении совместного действия нескольких сил рассматривают действие каждой из них в отдельности, а затем полученные результаты складывают, причем порядок рассмотрения сил при этом значения не имеет.
Однако следует иметь в виду, что пределы применения этого принципа ограничены. Он вполне применим лишь для тел абсолютно твердых или для таких, которые под действием внешних сил получают настолько малые деформации, что последние исчезают, как только внешние нагрузки перестают действовать на тело. Порядок аналитического расчета фермы методом вырезания узлов следующий:
1) обозначаем узлы заданной фермы буквами, а стержни— цифрами;
2) удаляем опоры и заменяем действие их на ферму опорными реакциями, пока нам неизвестными;
3) вырезаем узлы фермы (вычерчиваем схему вырезанных узлов);
4) составляем уравнения равновесия для отдельных узлов фермы (ΣХi=0; ΣYi = 0), вначале предполагая, что все стержни фермы растянуты (усилия направлены от узлов); порядок перехода от узла к узлу обусловливается требованием, чтобы в рассматриваемом узле было не более неизвестных сил;
5) решаем эти уравнения равновесия и определяем величину и знак искомых усилий в стержнях.
- Геометрически изменяемые и неизменяемые системы.
Геометрически неизменяемой называют систему, изменение формы которой возможно только вследствие деформации составляющих ее элементов (или изменения размеров элементов, или изменения их размеров и формы). Так, шар-нирно-стержневой треугольник ABC (рис. 41.1, А) При узловой передаче нагрузки деформируется в результате изменения длины стержней АВ, ВС, СА, А система с жесткими узлами (рис. 41.1, Б) — Вследствие одновременного изменения длины и искривления стержней АВ, ВС, СА.
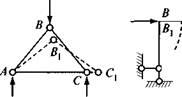

Рис. 41.1. Геометрически неизменяемые и изменяемые системы
Геометрически изменяемой называют систему, форма которой может меняться без деформации составляющих ее элементов.
Простейшая геометрически изменяемая система изображена на рис. 41.1, В. Она состоит из трех стержней — АВ, ВС, CD, Соединенных между собой и прикрепленных к неподвижному телу шарнирами. Если, например, к узлу В Такой системы приложить даже малую нагрузку, то система придет в движение и без деформации составляющих ее элементов займет положение ABXCXD, Показанное на рисунке штрихпунктирными линиями. Если принять АВ = ВС, То конечное и начальное положения элемента CD Совпадут.
- Степень свободы и кинематические связи.
Перед расчетом реального сооружения после того как выбрана расчетная схема, необходимо провести кинематический анализ сооружения, цель которого установить, изменяемо оно или нет. Кинематический анализ начинается с определения степени свободы системы. Степенью свободы системы называется кинематическая характеристика, представляющая наименьшее число независимых параметров, с помощью которых можно определить положение всех точек системы в любой момент времени.
Например, положение точки на плоскости определяется двумя координатами, поэтому степень свободы точки на плоскости равна двум. Всякое устройство, не допускающее изменения взаимного положения точек или сечений системы, называется связью. Устройство, уменьшающее степень свободы на единицу, рассматривается как одна кинематическая связь. Если система обладает определенной степенью свободы, то для ликвидации ее подвижности необходимо в систему внести дополнительные связи, общее число которых должно быть не менее степени свободы системы
Под кинематической группой понимается механизм (устройство), который создает отдельное исполнительное движение с заданными параметрами, определяющими траекторию, путь, скорость и направление движения, положение начала движения и относительное геометрическое положение траектории создаваемого исполнительного движения.
Структура любой кинематической группы всегда состоит из внутренней и внешней кинематических связей. Внутренняя связь, обеспечивающая заданную траекторию исполнительного движения, может состоять только из одной кинематической пары ■— простая группа —-или из нескольких пар и кинематических цепей, соединяющих подвижные исполнительные звенья этих пар между собой, — сложная группа. В последнем случае число внутренних кинематических цепей, из которых состоит внутренняя кинематическая связь, на единицу меньше числа элементарных движений, входящих в состав создаваемого группой исполнительного движения.
Внутренняя кинематическая связь сама, .без источника движения, создать исполнительное движение, конечно, не может;, ее задача — согласовать параметры элементарных движений так, чтобы, если во внутренней связи движение возникло, то исполнительное движение происходило бы по заданной траектории.
Таким образом, под внутренней или исполнительной связью понимается кинематическая связь, обеспечивающая траекторию исполнительного движения. Но в кинематической группе нужно еще движение, создаваемое каким-либо отдельным для этой группы или общим для всего станка источником движения. Как известно, в качестве источников движения в металлорежущих станках широко применяются электро- и гидродвигатели, реже — пневматические и другие двигатели. Не рассматривая устройство и принципы работы этих двигателей — это не входит в задачу структурного анализа металлорежущих станков, — необходимо подчеркнуть лишь то, что в каждом двигателе имеются две части: одна, в которую подводится энергия, и другая, в которой возникает исходное движение на выходном звене. Будем в дальнейшем различать и условно называть первую часть двигателя его энергетической частью, а вторую — механической частью двигателя. С выходного звена двигателя снимается исходное движение и дальше по внешней связи (по цепям привода) передается во внутреннюю связь группы.
- Многопролетные статически определимые балки. Типы шарнирных балок.
Многопролетные статически определимые балки представляют собой совокупность однопролетных консольных балок, соединенных между собой шарнирами. В практике строительства этот вид балок (как и многопролетные бесшарнирные неразрезные балки) применяется для перекрытия нескольких смежных пролетов. Использование для этой цели последовательно уложенных однопролетных статически определимых балок менее рационально, так как при равной нагрузке усилия в них выше, чем в неразрезных или многошарнирных балках, что приводит к излишнему расходу материала и утяжелению конструкции. По сравнению с неразрезными балками многошарнирные статически определимые балки обладают всеми преимуществами, свойственными статически определимым системам. В- частности, распределение усилий в статически определимых системах не зависит от жесткости отдельных элементов; в таких системах не возникают температурные и монтажные напряжения. Они имеют также ряд других достоинств, что и обусловило их широкое применение в строительстве.
Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов. 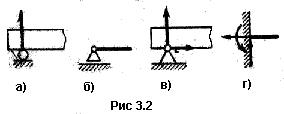
1. Подвижная шарнирная опора (рис. 3.2, а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка.
Схематичное изображение подвижной шарнирной опоры дано на рис. 3.2, б.
Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений.
2. Неподвижная шарнирная опора (рис. 3.2, в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие - горизонтальную и вертикальную.
3. Жесткая заделка, или защемление (рис. 3.2, г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент).
Балка с одним заделанным концом называется консольной балкой или просто консолью.
Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения - уравнения перемещений.
- Схемы взаимодействия элементов, составляющих шарнирные балки.
Анализ расчетных схем многопролетных статически определимых балок показывает, что всегда в этих балках можно выделить два вида несущих элементов: основные и второстепенные.
К основным элементам, называемым основными балками, относятся бесшарнирные балки, обеспечивающие геометрическую неизменяемость всей системы в целом. Кроме нагрузки, действующей непосредственно на основные балки, последние воспринимают частично или полностью нагрузку, приложенную к второстепенным элементам.
К второстепенным элементам, иначе называемым подвесными балками, относятся элементы, опирающиеся на. основные балки и передающие на них нагрузку.
Аналитический расчет многопролетных статически определимых балок заключается в последовательном расчете составляющих эти балки отдельных несущих элементов. Для этого прежде всего выявляются основные и второстепенные элементы и устанавливается схема их взаимодействия, для чего составляется поэтажная схема расчета. При составлении этой схемы вначале вычерчиваются основные балки, а затем в этажном порядке — второстепенные.
В многопролетных балках с чередующимися бесшарнирными и двухшарнирными пролетами число основных балок равно числу бесшарнирных пролетов, а расчетная схема является двухэтажной. При составлении поэтажной схемы расчета для этого типа балок для обеспечения геометрической неизменяемости к опорам основных балок добавляются лишние стержни.
Многопролетные балки с чередующимися одношарнирными пролетами имеют только одну основную балку, а число этажей в поэтажной схеме расчета равно общему числу несущих элементов.
Для других возможных типов многопролетных балок поэтажные схемы расчета будут иными.
Расчет многопролетных балок всегда ведут с второстепенных элементов в нисходящем порядке. При расчете нижних этажей необходимо учитывать дополнительную нагрузку на консоли от верхних этажей. После расчета второстепенных элементов рассчитывают основные. Окончательные эпюры объединяются на одном чертеже.
- Аналитический способ расчета трехшарнирных арок.
Трехшарнирная арка является системой геометрически неизменяемой и статически определимой.
В практике встречаются различные по форме и виду арки.
В том случае, когда каждая половина трехшарнирной арки представляет собой сплошной брус криволинейного очертания, ее называют аркой с
В практике встречаются арки, образованные из двух ферм, соединенных между собой общим шарниром с.
При действии внешней нагрузки на трехшарнирную арку (рис.
Кроме трех уравнений равно- веси я, которые дает статика для системы сил, расположенных^-в одной плоскости, для расчета трех-шарнирной арки можно составить четвертое уравнение, основанное на том, что равнодействующая всех сил, приложенных к левой (а также и к правой) половине арки, должна пройти через средний шарнир с, так как в противном случае левая (или правая) половина арки вращалась бы вокруг точки с.
то четвертое уравнение статики можно сформулировать следующим образом: алгебраическая сумма моментов сил, действующих на левую или правую половину арки относительно точки с {среднего шарнира), равняется нулю, т.
Таким образом, при расчете трехшарнирной арки можно составить следующие четыре уравнения:
1) (Есе силы, действующие на арку, проецируются на ось х)\?
3) (составляется сумма моментов всех сил, действующих на арку, относительно произвольной точки; удобно в качестве такой точки принимать точку а или 6); или
Полученные для Va и Vb формулы пок-аэывают, что при действии на арку вертикальной нагрузки вертикальные составляющие опорных реакций соответственно равны опорным реакциям простой двухопорной балки с пролетом, равным пролету арки (рис.
Из этого равенства заключаем, что распоры, возникающие на опорах при действии на арку вертикальной нагрузки, равны между собой.
Таким образом, распор арки равен изгибающему моменту в сечении с абсциссой х = 1\ простой двухопсрной балки (с пролетом, равным пролету арки), разделенному на стрелу подъема /.
Для определения распора Н составим выражение суммы моментов сил, действующих на левую половину арки, относительно шарнира с: отк\гда
был предложен расчет упругой арки методами теории упругости; он одним из первых использовал в строительной механике «принцип наименьшей работы».
Для определения горизонтальной реакции На составим выражение для момента всех сил, действующих на левую половину арки, относительно шарнира с: откуда
Определение внутренних усилий в арке при произвольной нагрузке
Внутренними усилиями являются: изгибающий момент М, поперечная сила Q и продольная сила N, действующие в поперечных сечениях арки.
Изгибающий момент считается положительным, если левые силы стремятся вращать арку относительно данного сечения по ходу.
Определим изгибающий момент в произвольном сечении k (абсцисса которого равна xk) арки, изображенной на рис.
Определим поперечную силу в сечении k арки, изображенной на рис.
Продольную силу считают положительной, если она в сечении арки вызывает сжатие.
Определим продольную силу в сечении k арки, изображенной на рис.
Арка очерчена по б е которой параболе, уравнение которой
Определение внутренних усилий в арке при вертикальной нагрузке
При действии на арку Этой формулой удобно пользоваться при построении эпюры моментов в арке, работающей на вертикальную нагрузку.
Рис- злз Заметим, что приведенная формула для Мхнаглядно показывает уменьшение изгибающего момента в арке по сравнению с балкой, что подтверждает экономичность арочной конструкции по сравнению с балочной.
Для этой цели спроецируем все приложенные слева силы сначала на нормаль к оси арки, а затем на касательную к ней в сечении с абсциссой х: cos фх—Н sin срх; ={Va—^P) sin ф.
В сечении k арки определить значения изгибающего момента М},, поперечной силы Q^ и продольной силы Л'^ ог действия нагрузки, показанной на рис.
Арка очерчена по параболе, уравнение которой
Кроме аналитических методов расчета арок существуют приемы решения этой же задачи, основанные на графических построениях.
Рассмотрим случай действия на арку, изображенную на рис.
Определим сначала опорные реакции от действия на арку силы Рг.
На левой опоре арки возникает реакция Alt Таким образом, вся арка в целом будет находиться в равновесии под действием трех сил: Alt Bt и Рх.
Аналогично определим реакции А2 и Bs, возникающие от силы Рг, действующей на правую половину арки (рис.
На основании принципа независимости действия сил, сложив геометрически найденные силы Аг и А2, Bt и В2, получим реакции А и В, возникающие на опорах трехшарнирной арки от сил Рг и Р2.
Рассмотрим теперь построение так называемого много\ гольника давления, с помощью которого можно определить внутренние усилия М, N и Q, возникающие в любом сечении арки.
Любая из сторон многоугольника давления совпадает с линией действия равнодействующей всех левых (или правых) сил в арке.
Следовательно, с помощью силового многоугольа)ника и многоугольника давления можно определить все внутренние усилия в любом сечении арки.
Составляющая 0—6 даст поперечную силу Q в сечении kx— k± арки, а составляющая 6—1 — продольную силу N в этом же сечении.
Линия давления дает наглядное представление о работе арки.
происходит распрямление оси арки.В случае действия на арку системы сосредоточенных сил Ри Р2, Ps и т.лев всех внешних активных сил (без опорных реакций), действующих на левую половину арки;находят равнодействующую Rnv всех внешних активных сил (без опорных реакций), действующих на правую половину арки;
Каждой нагрузке, действующей на данную трехшарнирную арку, соответствует только один многоугольник давления.
При действии на арку сплошной нагрузки многоугольник давления превращается в кривую давления.
Совершенно очевидно, что если арке дать очертание, при котором ее ось совпадает с многоугольником давления от заданной на грузки, то в такой арке не возникнут ни изгибающие моменты, ни поперечные силы.
В этом случае арка будет работать исключительно на сжатие, что весьма выгодно, в особенности для каменных и бетонных сооружений.
Такое очертание оси арки называется рациональным х определение внутренних сил в арке.При действии на арку только вертикальных сил горизонтальная составляющая любой из равнодействующих левых (или правых) сил равняется распору Я (полюсному расстоянию) \ Поэтому, если через какую-либо точку k оси арки
- Определение деформаций и перемещений в статически определимых плоских системах. Формула Мора для элемента сооружения.
Суть метод Мора в следующем. Если необходимо определить перемещение в заданной точке по заданному направлению, то наряду с заданной системой внешних сил в этой точке прикладывается внешнее усилие Ф = 1 в интересующим нас направлении.
Далее составляется выражение потенциальной энергии системы, состоящей из n участков с учетом одновременного действия заданной системы внешних сил и силы Ф :

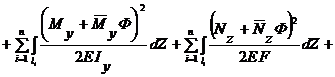 (6.1)
(6.1)
 ,
,
где Кх , Ку - безразмерные величины, зависящие от геометрической формы сечения и учитывают неравномерность распределения касательных напряжений в сечении при поперечном изгибе. Так, например, для прямоугольника Кх = Ку = 1,2, а для двутавра при изгибе в плоскости его стенки K = F/FCT , где F - площадь всего сечения двутавра, FCT - площадь стенки; Nz , Qx , Qy , Mz , Mx , My - внутренние силовые факторы, возникающие в поперечных сечениях заданной стержневой системы; 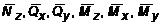 -внутренние силовые факторы, возникающие в поперечных сечениях заданной системы, от действия усилия Ф = 1.
-внутренние силовые факторы, возникающие в поперечных сечениях заданной системы, от действия усилия Ф = 1.
Дифференцируя выражение (6.1) по Ф, и полагая после этого Ф = 0, находим искомое перемещение в искомой точке в нужном направлении.
- Общие
