Отбраковка полученных данных
| № п/п | 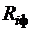 | 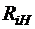 | 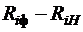 | 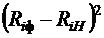 | 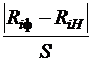 |
| 34,2 | 35,1 | -0,9 | 0,7 | 0,40 | |
| 32,3 | 34,6 | -2,3 | 5,4 | 1,08 | |
| 33,3 | 32,7 | 0,6 | 0,3 | 0,26 | |
| 31,5 | 2,5 | 6,1 | 1,15 | ||
| 31,7 | 31,8 | -0,1 | 0,0 | 0,02 | |
| 35,1 | 30,0 | 4,2 | 17,6 | 1,95 | |
| 34,2 | 35,4 | -1,2 | 1,4 | 0,55 | |
| 32,5 | 34,9 | -2,4 | 6,0 | 1,14 | |
| 32,9 | 32,7 | 0,2 | 0,0 | 0,08 | |
| 31,2 | 2,8 | 7,6 | 1,29 | ||
| 17,9 | 18,7 | -0,8 | 0,6 | 0,35 | |
| 16,5 | 17,3 | -0,8 | 0,7 | 0,39 | |
| 13,4 | 12,8 | 0,6 | 0,3 | 0,26 | |
| 17,1 | 19,6 | -2,5 | 6,2 | 1,15 | |
| 13,5 | 12,0 | 1,5 | 2,4 | 0,72 | |
| 10,3 | 10,2 | 0,1 | 0,0 | 0,06 | |
| 18,5 | 18,7 | -0,2 | 0,0 | 0,07 | |
| 16,5 | 16,7 | -0,2 | 0,1 | 0,11 | |
| 15,8 | 13,7 | 2,1 | 4,4 | 0,97 | |
| 13,9 | 17,9 | -4,0 | 15,9 | 1,85 | |
| 24,38 | 83,3 |
Далее необходимо определить остаточное среднее квадратическое отклонение по формуле (12):
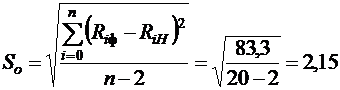 .
.
После этого необходимо модуль каждой разности частной фактической прочности и частной расчетной прочности разделить на остаточной среднее квадратическое отклонение по формуле (13). Получаемые значения удобно добавить в таблицу П5.
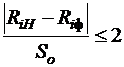 .
.
Если окажется, что какое-либо вычисление меньше или равно 2 то та фактическая прочность бетона, для которой производилось вычисление, признается браком, и ее необходимо исключить из исходных данных, из таблицы 3. После исключения брака необходимо произвести корректировку средних значений фактической прочности и косвенной величины, а также корректировку коэффициентов a и b, и уравнения градуировочной зависимости, кроме того следует произвести расчет новых значений расчетной прочности и построить новую градуировочную зависимость, а также следует произвести корректировку остаточного среднего квадратического отклонения.
В рассматриваемом случае ни одно вычисление по формуле (30) не потребовало отбраковки.
Если была произведена отбраковка некоторых экспериментальных данных или она не потребовалась то можно приравнять остаточное среднее квадратическое отклонение к среднему квадратическому отклонению построенной градуировочной зависимости по формуле (12):
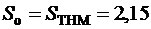 .
.
Затем следует рассчитать квадраты частной расчетной прочности и средней расчетной прочности бетона а также их сумму, кроме того, сумму произведений разностей частной расчетной прочности и средней расчетной прочности и частной фактической прочности и средней фактической прочности. Получаемые данные удобно свести в таблицу П6.
Таблица П6
Определение коэффициента корреляции
| № п/п | 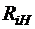 | 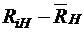 | 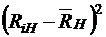 | 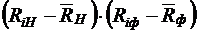 |
| 35,1 | 10,7 | 114,1 | 104,9 | |
| 34,6 | 10,3 | 105,1 | 81,2 | |
| 32,7 | 8,4 | 69,7 | 74,5 | |
| 31,5 | 7,1 | 51,0 | 68,7 | |
| 31,8 | 7,4 | 54,4 | 54,0 | |
| 30,1 | 5,7 | 32,5 | 61,1 | |
| 35,4 | 11,0 | 121,0 | 108,0 | |
| 34,9 | 10,6 | 111,7 | 85,8 | |
| 32,7 | 8,4 | 69,7 | 71,2 | |
| 31,2 | 6,9 | 47,0 | 65,9 | |
| 18,7 | -5,7 | 32,7 | 37,1 | |
| 17,3 | -7,0 | 49,6 | 55,5 | |
| 12,8 | -11,5 | 133,0 | 126,6 | |
| 19,6 | -4,8 | 23,0 | 34,9 | |
| 12,0 | -12,4 | 154,4 | 135,2 | |
| 10,2 | -14,2 | 201,9 | 200,1 | |
| 18,7 | -5,7 | 32,7 | 33,6 | |
| 16,7 | -7,6 | 58,5 | 60,3 | |
| 13,7 | -10,7 | 113,9 | 91,6 | |
| 17,9 | -6,5 | 42,2 | 68,1 | |
| 24,38 | 1618,4 | 1618,4 |
После этого можно рассчитать коэффициент корреляции по формуле (14):
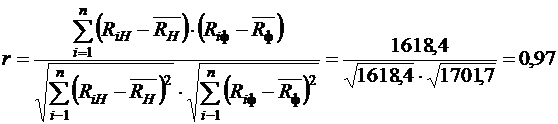 .
.
Если окажется, что коэффициент корреляции составит меньше 0,7 (r < 0,7), то применять полученную зависимость не допускается.
Кроме того если не выполняется условие (13.)
3. Определение класса бетона по прочности по результатам ультразвукового контроля.
Теперь по полученной градуировочной зависимости можно определить прочность бетона третьей серии образцов. Это можно сделать последовательной подстановкой в уравнение градуировочной зависимости (27) имеющихся косвенных величин, полученных в результате испытаний образцов третьей серии. Получаемые данные удобно свести в таблицу П7.
Таблица П7
