Вопрос 26. Архитектуры векторной обработки.

Классификация М. Флинна является одной из самых ранних и наиболее известных классификацией архитектур вычислительных систем. В основу классификации положено понятие потока. Поток - это последовательность, под которой понимается последовательность данных или команд, обрабатываемых процессором. Рассматривая число потоков данных и потоков команд, М. Флинн предложил рассматривать следующие классы архитектур: MIMD, SIMD, SISD, MISD.

SingleInstructionSingleData [stream] - "один поток команд, один поток данных", архитектура SISD (ОКОД). Описание архитектуры компьютерной системы, подразумевающее исполнение одним процессором одного потока команд, который обрабатывает данные, хранящиеся в одной памяти (рис. 8.1а.).

MultipleDatastreamprocessing - "один поток команд, много потоков данных", архитектура SIMD (ОКМД). Описание архитектуры параллельной компьютерной системы, подразумевающее исполнение одной текущей команды несколькими процессорами. Эта команда выбирается из памяти центральным контроллером SIMD-системы, но работает она над разными элементами данных (чаще всего - элементами массива). Для этого каждый процессор имеет ассоциированную с ним память, где хранятся массивы однородных данных. В эту категорию попадают, в частности, векторные процессоры. (рис. 8.1б.).

MultipleInstructionSingleData[stream] - "много потоков команд, один поток данных", архитектура MISD (МКОД). Одна из четырёх возможных архитектур параллельного компьютера в классификации М. Флинна. В этой архитектуре данные подаются на набор процессоров, каждый из которых исполняет свою программу их обработки. Подобная архитектура ещё никогда не была реализована (рис. 8.1в.).

MultipleInstructions - MultipleData [stream] - "много потоков команд, много потоков данных", архитектура MIMD (МКМД). Одна из четырёх возможных архитектур параллельного компьютера. В этой архитектуре набор процессоров независимо выполняет различные наборы команд, обрабатывающих различные наборы данных. Системы в архитектуре MIMD делятся на системы с распределённой памятью (слабо связанные системы), к которым относятся кластеры, и системы с совместно используемой памятью (shared-memorymultiprocessors). К последним относятся симметричные мультипроцессорные системы.

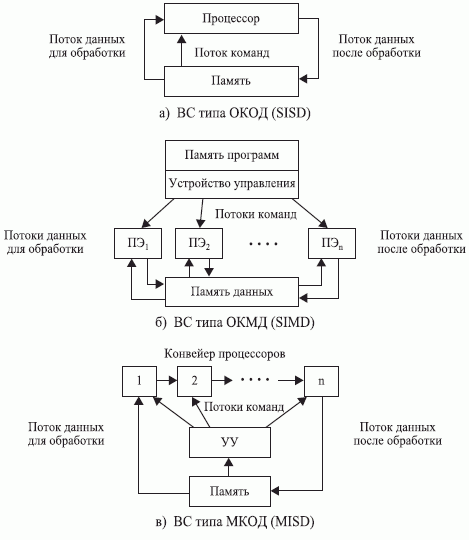
Рис. 8.1 Классификация М. Флинна

В класс SISD входят однопроцессорные последовательные компьютеры. Векторно-конвейерные компьютеры также могут быть отнесены к этому классу, если рассматривать вектор как одно неделимое данное для машинной команды. Это отмечают критики этой классификации.

Согласно классификации Флинна, к классуSIMDотносятся ВС, где множество элементов данных подвергается параллельной, в однотипной обработке.SIMD-системы во многом похожи на классические фон-неймановские ВМ: в них также имеется одно устройство управления, обеспечива­ющее последовательное выполнение команд программы. Различие касается стадии выполнения, когда общая команда транслируется множеству процессоров (в простейшем случае — АЛУ), каждый из которых обрабатывает свои данные

В настоящее время принято считать, что класс SIMDсоставляют векторные (векторно-конвейерные), матричные, ассоциативные, систолические иVLIW-вычислительные сис­темы.

В средствах векторной обработки под вектором понимается одномерный массив однотипных данных (обычно в форме с плавающей запятой), регулярным образом размещенных в памяти ВС. Если обработке подвергаются многомерные массивы, их также рассматривают как векторы.. Пусть имеется массив данныхA, представляющий собой прямоугольную матрицу размерности 4x5 (рис. 8.2).

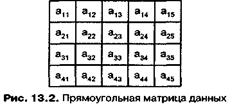
Рис.8.2. Прямоугольная матрица данных

При размещении матрицы в памяти все ее элементы заносятся в ячейки с последовательными адресами, причем данные могут быть записаны строка за строкой или столбец за столбцом (рис. 8.3). С учетом такого размещения многомерных массивов в памяти вполне допустимо рассматривать их как векторы и ориентировать соответствующие вычислительные средства на обработку одномерных мас­сивов данных (векторов).

Действия над многомерными массивами имеют свою специфику. Например, двумерном массиве обработка может вестись как по строкам, так и по столбцам. Это выражается в том, с каким шагом должен меняться адрес очередного выбираемого из памяти элемента. Так, если рассмотренная в примере матрица расположена в памяти построчно, адреса последовательных элементов строки различаются на единицу, а для элементов столбца шаг равен пяти. При размещении матрицы по столбцам единице будет равен шаг по столбцу, а шаг по строке — четырем. В векторной концепции для обозначения шага, с которым элементы вектора извлекаются из памяти, применяют термин шаг по индексу (stride).

Еще одной характеристикой вектора является число составляющих его элементов — длина вектора.