Тень фронтально-проецирующей прямой

Пусть дан отрезок [AB], перпендикулярный плоскости V (гвоздь) (рис. 11). Поскольку точка В 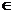V b' = b_T'.

Построим тень точки А, проведя через нее луч, параллельный S. Соединив одноименные проекции точек b_T' и а_Т' получим тень гвоздя на плоскости V.

Рис. 11. Построение тени гвоздя

Тень прямой, параллельной плоскости проекций

Дано: отрезок [AB]∥V. Из рис. 12 следует, что обе тени концов отрезка будут отброшены на фронтальную плоскость проекций, поэтому на основании свойства параллельных проекций можно сделать

вывод: тень отрезка прямой, на параллельную ему плоскость, равна и параллельна самому отрезку.

Символическая запись этого вывода выглядит следующим образом:

а_Т' b_Т'∥а' b' а_Т' b_Т' = а' b'

Рис. 12. Тень прямой уровня

Тень прямой общего положения

Пусть отрезок [AB] занимает в пространстве общее положение
(рис. 13). Тогда множество лучей, проходящих через [AB] образует плоскость общего положения, следы которой P_H и P_V будут являться тенями этого отрезка на плоскостях проекций H и V. Для решения задачи использована мнимая тень точки B.

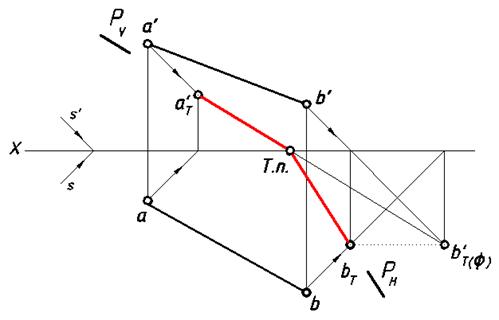
Рис. 13. Тени отрезка [AB]

Тени плоских фигур

До сих пор нами рассматривались геометрические образы, у которых могли быть только падающие тени. У фигур, ограниченных плоскими отсеками, наряду с падающими тенями будут существовать и собственные, поскольку плоскость – двусторонняя поверхность.

Рассмотрим отсеки плоских фигур (треугольника и круга), соответственно параллельные плоскостям V и H. Очевидно, что при заданном направлении светового потока,неосвещенные стороны отсеков плоскостей на соответствующих проекциях будут закрыты оригиналами.

Совокупность сторон треугольника представляет собой контур собственной тени. Лучевые плоскости, проходящие через стороны треугольника, образуют призматическую поверхность, которая, пересекая плоскость V, образует на ней фигуру, равную данному треугольнику, поскольку (ABC)∥V. Построение падающей тени треугольного отсека показано на рис. 14.

На основании этих построений можно сделать

вывод: граница падающей тени плоской фигуры является тенью от контура собственной тени этой фигуры.

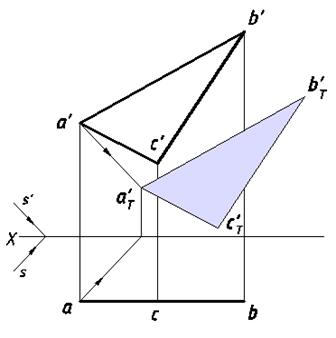
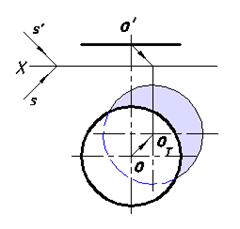
Рис. 14. Падающая тень треугольника Рис. 15. Падающая тень круга

Множество световых лучей, проходящих через каждую точку окружности другого плоского отсека, образуют поверхность эллиптического цилиндра, которая пересекает плоскость H по окружности.

Окружность-оригинал и падающую тень круга на плоскости H можно считать параллельными сечениями светового эллиптического цилиндра. Для нахождения местоположения падающей тени следует определить действительную тень центра данного круга на плоскости H (рис. 15).

Аналогичные рассуждения можно провести для нахождения падающей тени круга, плоскость которого параллельна плоскости V (рис. 16).

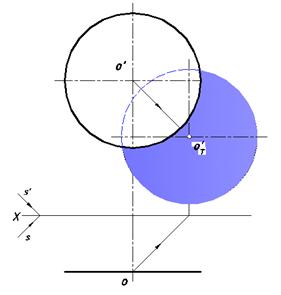
Рис. 16. Тень круга на плоскости V

Вывод: тень плоской фигуры, на параллельную ей плоскость, равна и параллельна одноименной проекции этой фигуры.

На рис. 17 дан эпюр плоскости (ABC), занимающей общее положение. В отличие от предыдущих примеров определение теневой стороны плоскости является самостоятельной задачей.

Для нахождения собственной тени плоского отсека поступим следующим образом. Возьмем случайную точку K(k, k') внутри треугольного отсека на случайной прямой, заведомо лежащей в этой плоскости. Проведем через эту точку прямую, параллельную направлению S.

Рассмотрим конкурирующие точки 1= (2'), принадлежащие стороне [AC] и проведенному лучу.

По горизонтальным проекциям 1 и 2 решаем вопрос о взаимной видимости плоской фигуры и прямой, проведенной через точку K(k, k').

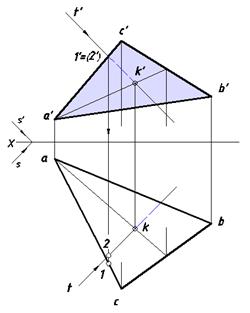
Рис. 17. Определение собственной тени треугольного отсека

Поскольку точка на стороне [AC] находится ближе к наблюдателю она перекрывает точку на вспомогательной прямой. Отсюда следует вывод о видимости, показанной на эпюре.

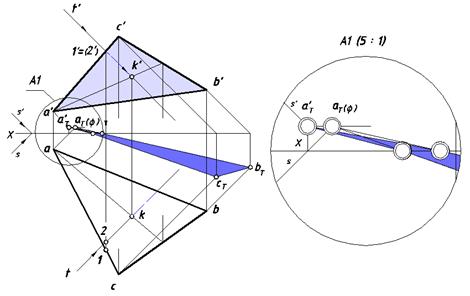
Рис. 18. Построение падающей тени треугольного отсека

Все множество лучей освещает плоскость (ABC) со стороны, невидимой наблюдателю, в собственной тени будет находиться сторона отсека, выделенная на эпюре цветом.

На приведенном выше рисунке построена падающая тень объекта.

Пусть дана плоскость круга, параллельная плоскости V (рис. 19). Собственная тень закрыта оригиналом. Реальная часть падающей тени на плоскости V представляет собой сегмент круга.

Лучевая поверхность эллиптического цилиндра, проходящая через окружность данного круга, пересекает плоскость H по эллипсу. Поскольку эллипс – лекальная кривая ее следует строить по множеству точек, две из которых являются точками преломления и лежат на оси X. Для нахождения случайных точек можно поступить следующим образом: описать квадрат вокруг данной окружности и построить его падающие тени.

Заметим, что точка А (а, а') одновременно принадлежит кругу
и квадрату, поэтому точка а_Т для эллипса является искомой. Построение еще двух случайных точек показано на чертеже.

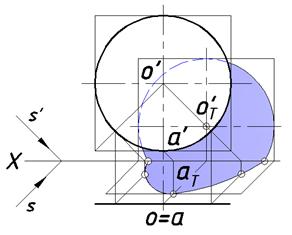
Рис. 19. Тень круга на двух плоскостях проекций

Рассмотрим задачи, связанные с построениями собственных и падающих теней на плоских фигурах.

З а д а ч а 1

Построить тень отрезка [MN] на плоскости (ABC).

Возможны различные подходы к решению поставленной задачи. Один из них состоит в том, что можно построить падающие тени данных оригиналов на плоскости проекций независимо друг от друга, а затем применить способ обратных лучей. На рис. 20 показаны эти построения. Далее определены точки 1_Т и 2_Т , общие для контура падающей тени треугольника и прямой, содержащей точки m_T и n_T.

По действительным теням 1_Т и 2_Т с помощью обратных лучей построены точки 1 и 2, а затем найдена горизонтальная проекция падающей тени отрезка [MN] на плоскость данного треугольника. С помощью линий связи на основании свойства инцидентности построены все недостающие фронтальные проекции точек.

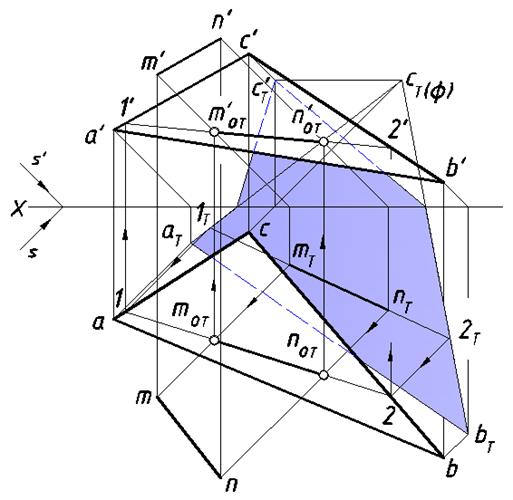
Рис. 20. Использование обратных лучей для решения задачи

Рассмотрим другой вариант решения задачи. Поскольку в данной задаче не ставится вопрос о нахождении падающих теней оригиналов можно воспользоваться классической задачей начертательной геометрии
о пересечении прямой с плоскостью (рис .21).

Лучевая плоскость, проходящая через отрезок [MN], согласно выводам, сделанным ранее, оставит след на плоскости в виде прямой линии. Любая прямая определяется парой несовпадающих точек, которыми можно считать точки пересечения световых лучей, проходящих через концы отрезка [AB].

Для их нахождения применим алгоритм классической задачи:

1. проведем через световой луч фронтально-проецирующую плоскость;

(луч, проходящий через точку M, заключен во фронтально-проецирующую плоскость P, а через точку N – во фронтально-проецирующую плоскость T)

2. построим линию пересечения данной и вспомогательной плоскости;

(на эпюре показаны проекции (12), (1'2') для плоскости P и (34)
и (3'4') для плоскости Т)

3. определим искомые точки пересечением данной и построенной прямых;

(на эпюре отмечены их горизонтальные и фронтальные проекции).

Искомая тень на плоскости (ABC) – отрезок [M_ON_O].

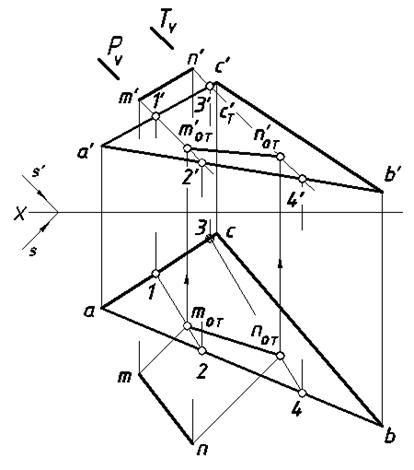
Рис. 21. Второй вариант решения задачи

З а д а ч а 2

Построить тень отрезка [MN] на плоскости параллелограмма (рис. 22).

Для решения задачи применим способ обратных лучей. Построим падающие тени отрезка [MN] и параллелограмма. Поскольку отрезок [AD]
и точка M принадлежат плоскости H

а = а_Т ; d = d_Т и m = m_Т.

У падающих теней данных оригиналов есть общие точки 1_Т
и 2_Т = 2_ОТ, по которым с помощью обратных лучей можно определить проекции искомых точек и линии пересечения.

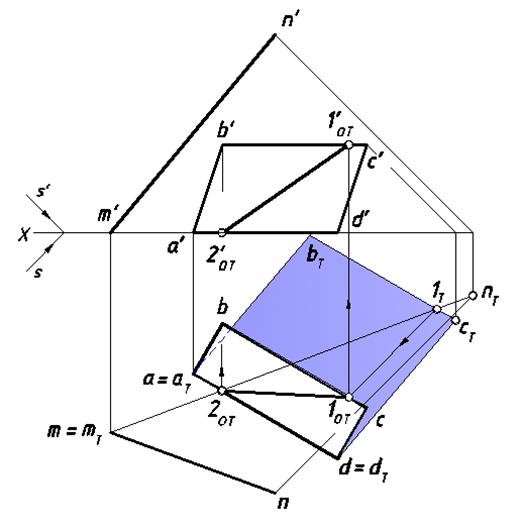
Рис. 22. Построение тени от одного объекта на другой

Заметим, что эту задачу также можно было решить и другим способом, изложенным в предыдущей задаче.

Тени геометрических тел

Тени многогранников

Пусть дана прямая призма, стоящая на плоскости H. Требуется построить ее собственные и падающие тени на плоскости проекций H
и V.(рис. 23). Проанализируем освещенность граней. При заданном направлении светового потока будут освещены верхняя и левая передняя грань. Остальные грани (в том числе и нижняя) находятся в тени. Для построения падающей тени объемного тела необходимо выявить контур собственной тени, который в данном случае будет представлять собой пространственную ломаную линию. Элементами этой линии являются ребра призмы, находящиеся на границах освещенных и неосвещенных плоскостей. На этом же рисунке представлено изометрическое изображение замкнутого контура собственной тени, от которого построена падающая тень.

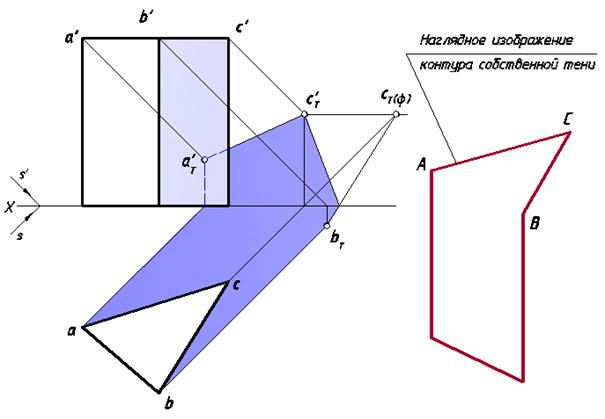
Рис. 23. Построение собственных и падающих теней призмы

Приведем задачи, связанные с построением теней многогранников.

З а д а ч а 1

Построить собственные и падающие тени пирамиды SABC; определить, какая часть отрезка [MN] отбросила тень на поверхность данного многогранника (рис. 24).

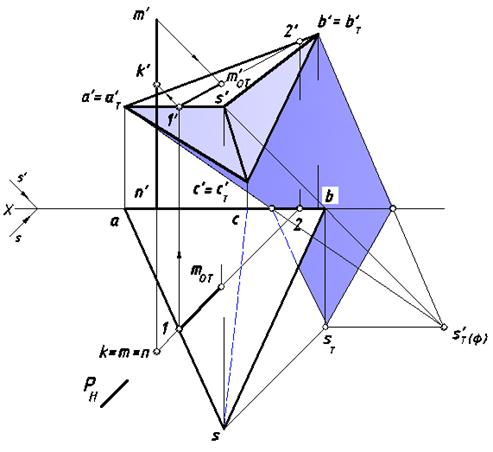
Рис. 24. Тень столба на поверхности пирамиды

При заданном направлении светового потока единственная грань пирамиды (ASB) будет освещена, остальные находятся в собственной тени. Контур собственной тени объекта – стороны треугольника ASB.

Для определения падающей тени столба на поверхность пирамиды заключим отрезок [MN] в горизонтально-проецирующую плоскость P, параллельную направлению светового потока. Эта плоскость пересечет освещенную грань пирамиды по прямой, проекции которой 12 и 1'2' показаны на чертеже. Поскольку луч, проходящий через точку M, находится
в этой же плоскости, то можно определить тень точки М на грани ASB. Отметим точку (1, 1') на ребре [AS], по которой с помощью обратного луча определим точку K(k, k') на отрезке [MN].

З а д а ч а 2

Определить освещенность видимых граней правильной шести угольной пирамиды (рис. 25).

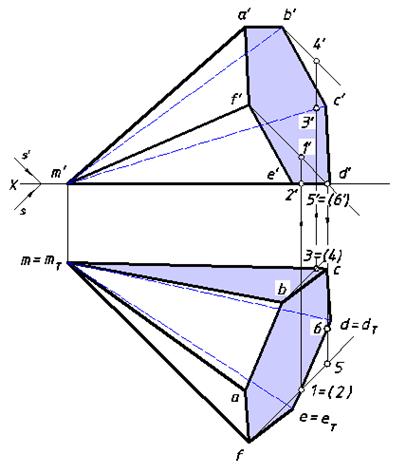
Рис. 25. Определение освещенности видимых граней

Заметим, что построение графического условия этой задачи – это уже задача, при решении которой целесообразно применить преобразование чертежа (на рис.25 эти построения не показаны). Видимость ребер на проекциях многогранника устанавливается с помощью конкурирующих точек.

Для нахождения контура собственной тени многогранников
в учебных источниках дается следующая рекомендация:

для многогранного тела достаточно провести лучи только через вершины и найти падающие тени от этих точек.

По сути дела предлагается вначале построить падающую тень, а по ней найти собственную.

На наш взгляд такой подход возможен, но не всегда приемлем, поскольку если у многогранника большое количество вершин, то многие падающие тени от последних могут оказаться внутри контура падающей тени многогранника и ряд построений окажется нецелесообразным. К сожалению, в учебной литературе по определению контура собственной тени многогранников довольно часто встречаются ошибки.

В задачах, рассмотренных ранее, определение освещенности граней не вызывает трудностей. Если количество видимых на эпюре граней многогранника велико или их освещенность не очевидна – рекомендуем применить метод конкурирующих точек для определения освещенности граней многогранников. Это позволит избежать ошибок при установлении контура собственной тени объекта и при этом выполнить минимальное количество построений.

Проведем световой луч через точку F(f, f') и рассмотрим конкурирующие точки, принадлежащие этому лучу и ребру [DE]. По аппликатам фронтальных проекций точек делаем заключение о видимости точек
1 = (2). Поскольку точка 2, находящаяся на ребре [DE], закрыта точкой 1 светового луча – она невидима, следовательно, вся 6-угольная грань пирамиды находится в тени. Отсюда можно сделать вывод об освещенности грани (AFM).

Часть луча, проходящего через вершину B(b, b') находится над гранью (BMC), что определяется с помощью конкурирующих точек 3 и 4, принадлежащих лучу и ребру [MC]. Устанавливаем, что 3 = (4) и делаем вывод о том, что эта грань находится в собственной тени, а грань (ABM) – освещена. Аналогичным образом анализируем освещенность остальных граней. Часто оказывается, что при установлении теневой грани отпадает необходимость проверки вершин многогранника, тени которых попадает
в область контура падающей тени.

Такой подход к определению видимости позволил избежать ошибки в аналогичной задаче в определении освещенности граней, допущенной в одном из учебников.

З а д а ч а 3

Построить собственные и падающие тени правильной шести угольной пирамиды (рис. 26).

Анализ видимых освещенных граней приведен в предыдущей задаче. В собственной тени будет находиться грань (DEM), расположенная
в плоскости H, следовательно, e = e_Т; d = d_Т и m = m_Т, т.е. три вершины пирамиды и их действительные тени на плоскости H совпадают.

Ребро [ME] входит в состав контура собственной тени пирамиды, т.к. грань(EFM) освещена.

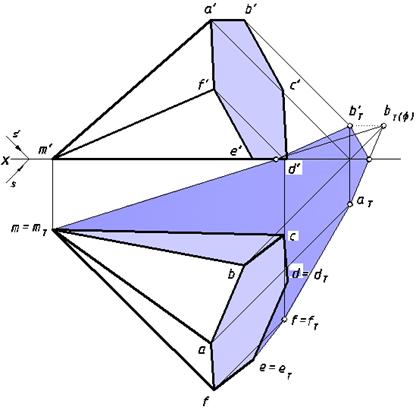
Рис. 26. Построение падающих теней пирамиды

Рассуждая аналогичным образом, определяем весь замкнутый контур собственной тени – это совокупная последовательность ребер
[ME] – [EF] – [FA] – [AB] – [BM]. От этих ребер определяем контур падающей тени данной пирамиды. Решение задачи показано на рис. 26.

Тени объемных тел,