Модели искусственного нейрона
Цель работы: изучение основных моделей искусственного нейрона, их математического описания, а также функционального и структурного графических представлений, исследование функций активации и рассмотренных моделей нейронов с помощью инструментального пакета имитационного моделирования Simulink системы MATLAB.
Теоретические сведения
Простой нейрон
Элементарной ячейкой нейронной сети является нейрон.
Структура нейрона с единственным скалярным входом показана
на рис. 3.1,а.
а б
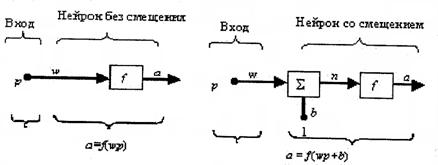
Рис. 3.1. Простой нейрон
Скалярный входной сигнал р умножается на скалярный весовой коэффициент w, и результирующий взвешенный вход w*p является аргументом функции активации нейрона, которая порождает скалярный выход а.
Нейрон, показанный на рис. 3.1,б, дополнен скалярным смещением b. Смещение суммируется со взвешенным входом w*p и приводит к сдвигу аргумента функции на величину b. Действие смещения можно свести к схеме взвешивания, если представить что нейрон имеет второй входной сигнал со значением, равным 1. Вход n функции активации нейрона по-прежнему остается скалярным и равным сумме взвешенного входа и смещения b. Эта сумма является аргументом функции активации f; выходом функции активации является сигнал а. Константы w и b являются скалярными параметрами нейрона. Основной принцип работы нейронной сети состоит в настройке параметров нейрона с тем, чтобы функционирование сети соответствовало некоторому желаемому поведению. Регулируя веса или параметры смещения, можно “научить” сеть выполнять конкретную работу; возможно также, что сеть сама будет корректировать свои параметры, чтобы достичь требуемого результата.
Уравнение нейрона со смещением имеет вид
a = f(w*p+b*l).
Как уже отмечалось, смещение b – настраиваемый скалярный параметр нейрона, который не является входом, а константа 1, которая управляет смещением, рассматривается как вход и может быть учтена в виде линейной комбинации векторов входа
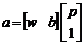 .
.
Функция активации
Функции активации (передаточные функции) нейрона могут иметь самый разнообразный вид. Функция активации f, как правило, принадлежит классу сигмоидальных функций с аргументом n и выходом а.
Ниже рассмотрены три наиболее распространенные функции активации.
Единичная функция активации с жестким ограничениям hardlim. Эта функция описывается соотношением а = hardlim(n) = 1(n) и показана на рис. 3.2. Она равна 0, если
n < 0, и 1,если n >= 0.
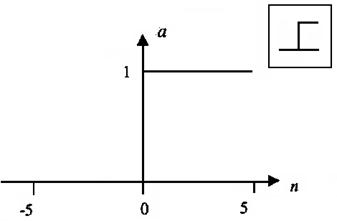
Рис. 3.2. Функция активации hardlim
В состав пакета ППП Neural Network Toolbox входит
М-функция hardlim, реализующая функцию активации с жесткими ограничениями.
Линейная функция активации purelin. Эта функция описывается соотношением а = purelin(n) = n и показана на рис. 3.3.
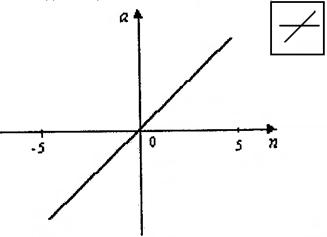
Рис. 3.3. Линейная функция активации purelin
Логистическая функция активации logsig. Эта функция описывается соотношением а = logsig(n) = 1/(1 + ехр(-n)) и показана на рис. 3.4. Она принадлежит к классу сигмоидальных функций, и ее аргумент может принимать любое значение в диапазоне
от 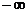 до
до 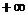 , а выход изменяется в диапазоне от 0 до 1. В пакете ППП Neural Network Toolbox она представлена М-функцией logsig. Благодаря свойству дифференцируемости эта функция часто используется в сетях с обучением на основе метода обратного распространения ошибки.
, а выход изменяется в диапазоне от 0 до 1. В пакете ППП Neural Network Toolbox она представлена М-функцией logsig. Благодаря свойству дифференцируемости эта функция часто используется в сетях с обучением на основе метода обратного распространения ошибки.
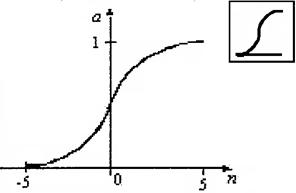
Рис. 3.4. Функция logsig
Символ в квадрате в правом верхнем углу графика характеризует функцию активации. Это изображение используется на структурных схемах нейронных сетей.
В пакет ППП Neural Network Toolbox включены и другие функции активации. Используя язык MATLAB, пользователь может создавать и свои собственные уникальные функции.
Нейрон с векторным входом
Нейрон с одним вектором входа р с R элементами 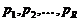 показан на рис. 3.5. Здесь каждый элемент входа умножается на веса
показан на рис. 3.5. Здесь каждый элемент входа умножается на веса 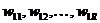 соответственно и взвешенные значения передаются на сумматор. Их сумма равна скалярному произведению вектора-
соответственно и взвешенные значения передаются на сумматор. Их сумма равна скалярному произведению вектора-
строки W на вектор входа р.
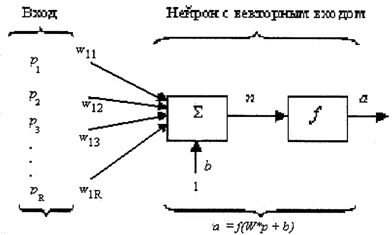
Рис. 3.5. Функциональная схема нейрона
Нейрон имеет смещение b, которое суммируется со взвешенной суммой входов. Результирующая сумма n определяется как
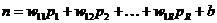
и служит аргументом функции активации f. В нотации языка MATLAB это выражение записывается так:
n = W*p + b.
Структура нейрона, показанная на рис. 3.5, содержит много лишних деталей. При рассмотрении сетей, состоящих из большого числа нейронов, будет использоваться укрупненная структурная схема нейрона (рис. 3.6).
Вход нейрона изображается в виде темной вертикальной черты, под которой указывается количество элементов входа R. Размер вектора входа р указывается ниже символа р и равен Rxl. Вектор входа умножается на вектор-строку W длины R. Как и прежде, константа 1 рассматривается как вход, который умножается на скалярное смещение b. Входом n функции активации нейрона служит сумма смещения b и произведения W*p. Эта сумма преобразуется функцией активации f, на выходе которой получается выходная величина нейрона а, которая в данном случае является скалярной величиной. Структурная схема, приведенная на рис. 3.6, называется слоем сети. Слой характеризуется матрицей весов W, смещением b, операциями умножения W*p, суммирования и функцией активации f. Вектор входов р обычно не включается в характеристики слоя.
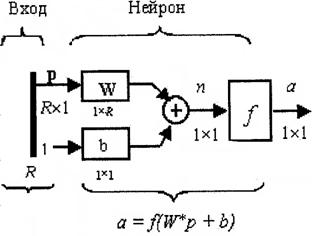
Рис. 3.6. Структурная схема нейрона
Каждый раз, когда используется сокращенное обозначение сети, размерность матриц указывается под именами векторно-матричных переменных. Эта система обозначений поясняет строение сети и связанную с ней матричную математику.
На укрупненной структурной схеме для обозначения типа функции активации применяются специальные графические символы; некоторые из них приведены на рис. 3.7, где а – ступенчатая; б – линейная; в – логистическая функция.
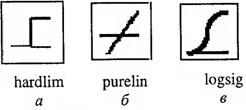
Рис. 3.7. Функции активации
Практические задания
Задание 1. Для функции активации с жесткими ограничениями hardlim и её производной dhardlim, определяемыми следующими соотношениями:
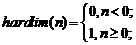
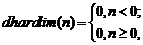
выполнить следующие действия:
1. Выдать на экран информацию об этих функциях с помощью следующих команд:
name=hardlim(′name′) % – полное название функции;
dname=hardlim(′deriv′) % – название производной;
inrange=hardlim(′active′) % – диапазон входа;
outrange=hardlim(′output′) % – диапазон выхода;
2. Построить графики функций:
n=-5:0,1:5;
a=hardlim(n);
da=dhardlim(n);
plot(n,a,′r′) % – график функции активации – красный;
Hard on
plot (n,da,′c′) % – график производной – голубой;
3. Рассчитать векторы выхода А и производной dA_dN для слоя из трёх нейронов с вектором входа N, состоящим из трёх компонентов:
N=[-0,7; 0,1; 0,8];
A=hardlim(N) % – вектор выхода функции актива;
dA_dN= dhardlim(N,A) % – вектор выхода производной.
4. Рассмотренную последовательность команд оформить в виде скрипта и записать в М-файл с именем hardlimfile.
Задание 2. Для симметричной функции активации с жёсткими ограничениями hardlims и её производной dhardlims, определяемыми соотношениями
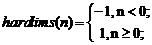
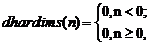
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файлпод именем hardlimsfile.
Задание 3.Для линейной функции активации purelin и ее производной, dpurelin, определяемыми соотношениями
рurelin = n;
dpurelin = 1,
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем purelinfile.
Задание 4. Для положительной линейной функции активации
poslin и ее производной dposlin, определяемыми соотношениями
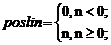
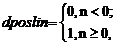
выдать на экран информацию об этих функциях, построить их
графики и рассчитать векторы выхода, воспользовавшись скриптом
из М-файла hardlimfile. Новый скрипт записать в файл под именем poslinfile.
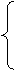 Задание 5. Для линейной функции активации с ограничениями saflin и ее производной dsaflin, определяемыми соотношениями
Задание 5. Для линейной функции активации с ограничениями saflin и ее производной dsaflin, определяемыми соотношениями
0, n < 0;
soflin(n) = n, 0 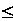 n
n 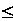 1;
1;
n, n > 0,
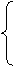 0, n < 0;
0, n < 0;
dsoflin(n)= 1, 0 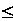 n
n 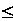 1
1
1, n > 0,
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем satlinfile.
Задание 6. Для симетричной линейной функции активации satlins с ограничениями и ее производной dsatlins, определяемыми соотношениями
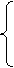 -1, n < -1;
-1, n < -1;
satlins(n) = n, -1 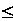 n
n 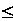 1;
1;
1, n > 1,
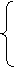 0, n < -1;
0, n < -1;
dsatlins(n) = 1, -1 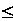 n
n 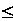 1
1
0, n > 1,
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем satlinsfile.
Задание 7. Для радиальной базисной функции активации radbas и ее производной dradbas, определяемыми соотношениями
radbas= e-2n,
dradbas= -2ne-2n,
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем radbasfile.
Задание 8. Для треугольной функции активации tribas и ее производной dtribas, определяемыми соотношениями
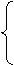 0, n < -1;
0, n < -1;
tribas(n) = 1-abs(n), -1 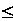 n
n 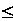 1;
1;
0, n > 1,
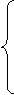
0, n < -1;
dtribas(n) = 1, -1 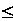 n
n 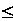 0
0
-1, 0 < n 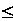 1
1
0, n > 1,
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем tribasfile.
Задание 9. Для логистической функции активации logsig и ее производной dlogsig определяемыми соотношениями
logsig(n) = 1 / (1 + e-n);
dlogsig(n) = e-n / (1 + e-n)2,
выдать на экран информацию об этих функциях, построить их
графики и рассчитать векторы выхода воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем logsigfile.
Задание 10. Для гиперболической тангенциальной функции активации tansig и ее производной dtansig определяемыми соотношениями
tansig(n) = 2 / (1 + e-2n) – 1;
dtansig(n) = 1 – tansig2(n),
выдать на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем tansigfile.
Задание 11. Для конкурирующей функции активации competиспользуемой для формирования вероятных и самоорганизующихся нейронных сетей выполнить следующие действия:
1. Выдать на экран информацию об этой функции с помощью следующего скрипта:
Name = compet(′name′) % – cometitive;
Dname = compet(′dеriv′) % – ″;
Inrange = compet(′active′) % – -in : inf;
Outrange = compet(′outrut′) % – 0 1.
2. Построить столбцовые диаграммы для вектора входа и для вектора выхода, используя слой из четырех нейронов:
N = [0; 1; - 0.5; 0.5];
A = compet(n);
subplot(2, 1, 1), % – подокна 2 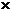 1; вывод в 1-е;
1; вывод в 1-е;
bar(n), % – столбцовая диаграмма;
ylabet(‘n’) % – метка оси ординат;
subplot(2, 1, 2), bar(a), ylabet(‘a’) % – во 2-м подокне.
3. Рассмотренную последовательность команд оформить в виде скрипта в М-файл с именем competlile.
Задание 12. Выполнить действия 11-го задания для конкурирующей функции активации с мягким максимумом softmax, записав при этом новый скрипт в М-файл с именем softmaxfile.
Задание 13. Для простого нейрона с одним двойным входом Р и функции активации hardlim подобрать весовой коэффициент W и смещение b таким образом, чтобы обеспечить инвертирование входного сигнала, т. е. замену нуля единицей, а единицы нулем.
Задание 14. Для нейрона с двумя двойными входами р1 и р2 и функцией активации hardlim подобрать весовые коэффициенты и смещение таким образом, чтобы нейрон выполнял функции логического сложения и логического умножения.
Задание 15. Для нейрона с двумя двойными входами р1 и р2 и функцией активацииhardlim подбирать весовые коэффициенты W11 и W12 и смещение b таким образом, чтобы классифицировать входные двойные наборы на два класса – нулевой и первый:
а) {00, 01} – нулевой класс, {10, 11} – первый класс;
б) {11} – нулевой класс, {00, 01, 10} – первый класс;
в) {00, 11} – нулевой класс, {01, 10} – первый класс;
г) {00, 11} – первый класс, {01, 10} – нулевой класс.
Задание 16. Для нейрона с двумя непрерывными входами р1 и р2 и функции активации hardlim построить график разделяющей линии, определяемой уравнением
W11p1 + W12p2 + b = 0,
считая, что значения весовых коэффициентов W11 W12 и смещения b заданы. Убедиться, что наборы входов р1 и р2 по разную сторону от разделяющей линии принадлежат разным классам и что не всякое множество наборов значений входов можно разделить на два класса, используя нейрон рассмотренного типа.
Задание 17. Используя блоки имитационного моделирования инструментального пакета Simulink системы MATLAB (блоки источников и регистраторов сигналов, математические и нелинейные блоки) построить рассмотренные в заданиях 1 – 16 модели нейронов, провести исследования моделей нейронов и оформить в электронном виде отчет с помощью генератора отчетов Simulink.
Лабораторная работа № 4
