Измерение расхода воды при помощи водосливов с тонкой стенкой

1. ЦЕЛЬ РАБОТЫ

Научиться на практике (в лабораторных условиях) способам из­мерения расхода воды при помощи водосливов с тонкой стенкой.

Произвести сопоставление опытных данных с расчетными, полу­ченными из формулы расхода. Исследовать коэффициент расхода во­досливов с тонкой стенкой.

2. ОБЩИЕ СВЕДЕНИЯ

Участок перегораживающего безнапорный поток сооружения, через который происходит перелив воды под воздействием силы тя­жести, называется водосливом, а течение жидкости на этом участке истечением через водослив.

Водосливы (рисунки 4.1, 4.2 и 4.3), у которых толщина стенки не влияет на форму переливающейся струи, относятся к водосливам с тонкой стенкой. У данных водосливов толщина стенки S>0,61H (где Н - геометрический напор на водосливе; S - толщина водослив­ной стенки).

Водосливы с тонкой стенкой часто применяются для измере­ния расхода воды в открытом потоке. При измерении расхода воды водосливами с тонкой стенкой необходимо чтобы соблюдалось сле­дующее: водослив должен быть неподтопленным; истечение свобод­ное; (давление вокруг струи атмосферное); скорость подхода доста­точно мала, чтобы её не учитывать; ребро порога должно быть выше дна подводящего канала.

Для определения расхода через водослив с тонкой стенкой пользуются формулой

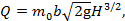(3.7)

где - расход жидкости через водослив, м³/с;

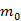- безразмерный коэффициент расхода водослива, учитывающий скорость подхода к водосливу;

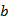- ширина водосливного фронта, м.

Для измерения расхода воды используют треугольные, трапецеидальные, прямоугольные (с боковым сжатием и без бокового сжатия) и параболические водосливы-водомеры.

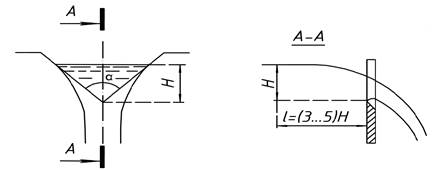
Рисунок 4.1 - Треугольный водослив с тонкой стенкой

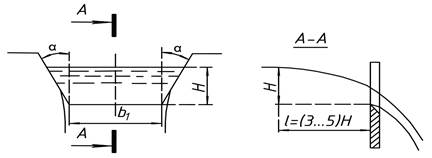
Рисунок 4.2 - Трапецеидальный водослив с тонкой стенкой

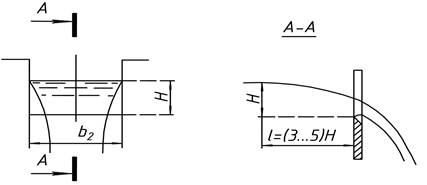
Рисунок 4.3 - Прямоугольный водослив с тонкой стенкой

Треугольными водосливами (рисунок 4.1) удобно поль­зоваться для измерения малых расходов. Их следует применять при напорах от 0,05 до 0,25 м. Для данных водосливов с прямым углом при вершине коэффициент расхода равен т₀ = 0,316.

Формула расхода (4.1) для треугольных водосливов при т₀ = 0,316 и g = 9,81 м/с² принимает вид

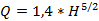(4.2)

Трапецеидальные водосливы (рисунок 4.2) использу­ются для измерения расхода воды в каналах и лабораторных лотках. Коэффициент расхода т₀ трапецеидального водослива зависит от угла α При а = 14° (tg а = 0,25) коэффициент т₀= 0,42. С учетом того, что т_о = 0,42 и g = 9,81 м/с² из выражения (4.1) получаем формулу расхо­да для трапецеидального водослива-водомера

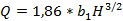(4.3)

Формулу (4.3) рекомендуется использовать, когда b₁ ≥ ЗН.

Расход через прямоугольный водослив (рисунок 4.3) определяется по формуле (4.1).

Коэффициент расхода прямоугольного водослива определяется по формулам:

- без бокового сжатия

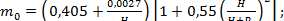(4.4)

- с боковым сжатием

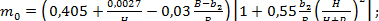(4.5)

где Р₁ - высота порога водослива со стороны верхнего бьефа, м;

В - ширина лотка (подводящего канала), м;

b₂ - ширина водосливного фронта, м;

H - геометрический напор, м.

Формулы (4.4) и (4.5) рекомендуется использовать при b₂ = 0,2...2 м; Р₂= 0,24... 1,13 м; Н = 0,05...1,24 м.

3. ОПИСАНИЕ ОПЫТНОЙ УСТАНОВКИ

На рисунке 1.1 представлена схема опытной установки. Вода по трубопроводу 1 подается в приемную камеру 3. При помощи за­движки 2 производится изменение расхода на треугольном водосливе- водомере 5. Пьезометр 4служит для определения напора на водосли­ве. В конце лотка 6 имеется паз 7, служащий для установки исследуе­мых водосливов с тонкой стенкой.

Для определения отметок дна лотка, гребня водослива и уровня воды используется шпиценмасштаб.

4. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТ

Устанавливается уклон дна лотка равным нулю. В конце лотка вставляется в паз 7 испытуемый водослив с тонкой стенкой. При по­мощи задвижки 2подается расход в лоток 6.

При установившемся движении жидкости измеряется расход воды. Расход Q определяется по тарировочной кривой водослива-водомера 5. Измеряется напор Н на исследуемом водосливе с тонкой стенкой на расстоянии l =3Н... 5Н от водослива в сторону верхнего бьефа (рисунки 4.1, 4.2 и 4.3).

5. ПОРЯДОК РАСЧЕТА

Расчет ведется в табличной форме (таблица 4.1).

1. Определяется напор над стенкой водослива (рисунок 4.1)

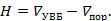
2. Находится расход воды для треугольного водослива по фор­муле (4.2); для трапецеидального водослива по формуле (4.3); для прямоугольных водосливов по формуле (4.1).

3. Сравнивается расходы водосливов, вычисленные по форму­лам (4.1), (4.2) и (4.3) для соответствующих водосливов с расходом по тарировочной кривой. Вычисляется процент расхождения расходов

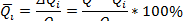
где Qi - расход по формуле (4.1) или (4.2), или (4.3).

4. Находятся опытные значения коэффициентов расхода т_оп, :

- для треугольного водослива

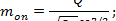
где Q - расход по тарировочной кривой, м³/с;

- для трапецеидального водослива

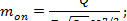
- для прямоугольного водослива с боковым сжатием

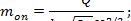
где В = 0,16 м - ширина лотка;

b₂ - ширина водосливного фронта (рисунок 4.3), м;

5. Вычисляются коэффициенты расхода по формулам (4.4) и (4.5) для прямоугольных водосливов, а для треугольного и трапецеи­дального водосливов коэффициенты расхода соответственно равны - 0,316 и 0,42.

6. Сравниваются коэффициенты расхода водосливов, получен­ные из опыта, с вычисленными их значениями. Определяется процент расхождения опытных данных и расчетных

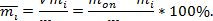
7. Сделать вывод по коэффициентам расхода водосливов с тонкой стенкой.

Таблица 4.1 - Опытные данные

Наименование	Водосливы
треуголь­ный	трапецеидальный	прямоугольный
с боковым сжатием	без бокового сжатия
1. Отметка дна, м
2. Отметка гребня водослива, м
3. Отметка уровня воды, м
4. Напор над стенкой Н, м
5. Ширина водослива b2, м
6. Ширина подводящего канала (лотка) В, м	0,16	0,16	0,16	0,16
7. Высота порога P1, м
8. Расход по тарировочной кри­вой, Q, м 3/с
9. Коэффициент расхода по формуле
10. Опытные значения коэффи­циентов топ
11. Процент расхождения опытных значений т и расчет­ных, %
12. Расход по формулам, м3/с
13. Процент расхождения опытного значения Q и расчет­ного

ЛАБОРАТОРНАЯ РАБОТА №5