Пропускная способность канала

Наибольшая возможная в данном канале скорость передачи информации называется его пропускной способностью. Пропускная способность канала есть скорость передачи информации при использовании «наилучших» (оптимальных) для данного канала источника, кодера и декодера, поэтому она характеризует только канал.

Номинальная скорость — битовая скорость передачи данных без различия служебных и пользовательских данных.
Эффективная скорость — скорость передачи пользовательских данных (нагрузки). Этот параметр зависит от соотношения накладных расходов и полезных данных.

Пропускная способность дискретного (цифрового) канала без помех

C = log m × Vт,

где m — основание кода сигнала, используемого в канале. Скорость передачи информации в дискретном канале без шумов (идеальном канале) равна его пропускной способности, когда символы в канале независимы, а все m символов алфавита равновероятны (используются одинаково часто). Vт - символьная скорость передачи.

Скорость передачи данных — объём данных, передаваемых за единицу времени^[1]. Максимальная скорость передачи данных без появления ошибок (пропускная способность) вместе с задержкой^[en] определяют производительность системы или линии связи. Теоретическая верхняя граница скорости передачи определяется теоремой Шеннона — Хартли.

Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона — Хартли утверждает, что ёмкость канала C, означающая теоретическую верхнюю границу скорости передачи информации, которые можно передать с данной средней мощностью сигнала S через один аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности N равна:

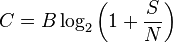
где

C — ёмкость канала в битах в секунду;

B — полоса пропускания канала в герцах;

S — полная мощность сигнала над полосой пропускания, измеренной в ваттах или вольтах в квадрате;

N — полная шумовая мощность над полосой пропускания, измеренной в ваттах или вольтах в квадрате;

S/N — отношение сигнала к гауссовскому шуму, выраженное как отношение мощностей.

Бит четности

В вычислительной технике и сетях передачи данных би́том чётности (англ. Parity bit) называют контрольный бит, служащий для проверки общей чётности двоичного числа (чётности количества единичных битов в числе).

В последовательной передаче данных часто используется формат 7 бит данных, бит чётности, один или два стоповых бита. Такой формат аккуратно размещает все 7-битные ASCII символы в удобный 8-битный байт. Также допустимы другие форматы: 8 бит данных и бит чётности.

В последовательных коммуникациях чётность обычно контролируется оборудованием интерфейса (например UART). Признак ошибки становится доступен процессору (и ОС) через статусный регистр оборудования. Восстановление ошибок обычно производится повторной передачей данных, подробности которого обрабатываются программным обеспечением (например, функциями ввода-вывода операционной системы)

Контроль некой двоичной последовательности (например, машинного слова) с помощью бита чётности также называют контролем по паритету. Контроль по паритету представляет собой наиболее простой и наименее мощный метод контроля данных. С его помощью можно обнаружить только одиночные ошибки в проверяемых данных. Двойная ошибка будет неверно принята за корректные данные. Поэтому контроль по паритету применяется к небольшим порциям данных, как правило к каждому байту, что даёт коэффициент избыточности для этого метода 1/8. Метод редко применяется в компьютерных сетях из-за невысоких диагностических способностей. Существует модификация этого метода — вертикальный и горизонтальный контроль по паритету. Отличие состоит в том, что исходные данные рассматриваются в виде матрицы, строки которой составляют байты данных. Контрольный разряд подсчитывается отдельно для каждой строки и для каждого столбца матрицы. Этот метод обнаруживает значительную часть двойных ошибок, однако обладает большей избыточностью. Он сейчас также почти не применяется при передаче информации по сети.

Расстояние по Хемменгу

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух слов одинаковой длины различны^[1]. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых q-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.

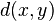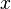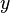Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга между двумя двоичными последовательностями (векторами) и длины 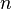называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в словарь алгоритмов и структур данных национального института стандартов и технологий США (англ. NIST Dictionary of Algorithms and Data Structures). Расстояние Хэмминга является частным случаем метрики Минковского (при соответствующем определении вычитания):

.

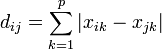Коды, исправляющие ошибки

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.

Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.

В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).

По способу работы с данными коды, исправляющие ошибки, делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.