Из истории исследования древнерусских измерительных инструментов
Из истории исследования древнерусских измерительных инструментов
О геометрических соотношениях саженей
Элементы золотых пропорций
Система древнерусских саженей
Модулор Корбюзье
Русская матрица
Вурфные отношения русской матрицы
Матричная вязь «Золотых скрижалей»
Понятие о живых фигурах
Логика древних саженей
Таинства церковного зодчества
Храм царя Соломона
Древнерусская метрология Египетских пирамид
Заключение
Литература
Об авторе
| ББК | 85.1я2 |
| Ч49 |
А.Ф. Черняев
Золото Древней Руси. Русская матрица - основа золотых пропорций.-М.: Белые альвы, 1998. -144 с., ил.
I SBN 5-7619-0062-9
Изучение взаимосвязей древнерусских саженей показало их кратность золотому числу Ф = 1,618. Необычный способ получения мерных частей саженей методом раздвоения-удвоения обусловил нахождение А.А. Пилецким древнерусского всемера - числовой матрицы многовариантного золотого пропорционирования. Исходя из нее построена русская матрица золотых пропорций - бесконечное поле взаимосвязанных степенных чисел, базирующихся на египетском ряде золотого сечения, которая лежит в основе многих математических магических построений. Степенная взаимосвязь каждого ряда чисел позволяет применять вурфные отношения для контроля самых различных материальных процессов. На ней основываются понятия живых и неживых фигур, методы системного пропорционирования, символика крестовых фигур и структура древних сооружений. Анализируются принципы церковного зодчества на примерах храмов XII -XVI вв. Объясняется непригодность для проживания объектов, пропорционированных метром.
Выяснилось, что зодчие Древнего Египта знали русскую матрицу, и все объекты древности, включая египетские пирамиды, проектировались и строились на основе комплекса древнерусских соизмерительных инструментов.
Издание снабжено изящными иллюстрациями, имеющими символический смысл и гармонично сочетающимися с текстом.
Книга рассчитана на архитекторов, дизайнеров, художников, строителей, историков, читателей, интересующихся применением метода золотых пропорций в различных областях знаний, а также специалистов и любителей древнерусской культуры.
| ISBN 5-7619-0062-9 | ©ЧерняевА.Ф., 1998. ©Гусельников А.В.,иллюстрации,,обложка,1998. ©"Белыеальвы", 1998. |
Первая работа "Золото Руси", посвященная золотым пропорциям в системе древнерусских измерительных инструментов, была издана в соавторстве с С.В.Тарасовой. За прошедшие три года найдено еще несколько методов, расширяющих представления о золотых пропорциях, и способов применения совершенно необычной системы мерных линеек как в Древней Руси, так и в Древнем Египте. Особенно существенным результатом стало некоторое понимание физических процессов, обусловивших необходимость одновременного использования нескольких видов мер при измерении одного и того же сооружения. И в частности, найден подход к объяснению живых и неживых фигур и соответствия им сооружаемых объектов.
Когда рукопись данной работы была передана в издательство, мне в руки попалась книга "Золотое сечение" И.Ш.Шевелева, М.А.Марутаева, И.П.Шмелева, в которой проводится анализ размерной структуры нескольких древнерусских церквей способом "парных мер" и предполагается, что мерило новгородского зодчего подтверждает наличие у древних зодчих системы парных мер.
Анализ размерной структуры тех же церквей методом "Всемера" А.А.Пилецкого выявил иную систему использования древних саженей, что обусловило необходимость внесения в работу нового раздела "Таинство церковного зодчества". В этом разделе показаны принципы пропорционирования, заложенные в мерило новгородского зодчего.
Новый материал, по мнению автора, представляет, значительный интерес как для специалистов, так и для самых разных читателей. За публикацию этой книги и сотворчество я выражаю свою искреннюю признательность издателю и редактору С.Н Удаловой и художнику А. В. Гусельникову.
ЭЛЕМЕНТЫ ЗОЛОТЫХ ПРОПОРЦИЙ
Откуда возникли представления о делении отрезков в крайнем и среднем отношениях, позволяющем получать золотое число Ф и пропорцию, названную Леонардо да Винчи «золотым сечением», нам неизвестно. Но уже в Древней Греции на основе золотого числа Ф - 1,618 посредством последовательного умножения (восходящая ветвь ряда) и деления (нисходящая ветвь ряда) базисной единицы на число Ф получали ряд из 11 чисел, имеющий название «золотого ряда», бесконечного в обе стороны:
...; 0,034; 0,056; 0,090; 0,146; 0,236; 0,382; 0,618; 1,000; 1,618; 2,618; 4,236; ... и т.д.
Каждое число этого ряда представляет собой иррациональную (бесконечную) последовательность цифр, округленных до 4 знаков. Каково собственное значение этих чисел и к какой геометрии они относятся — неизвестно тоже, а потому числа эти стоят на обочине и геометрии, и физики.
Однако уже древние греки поняли, что есть в этих числах какая-то особенность, проявляющаяся в том, что объекты, построенные с учетом золотых пропорций, обладают высокими эстетическими качествами и благотворно влияют на человека. И в наше время обнаруживается, что все процессы, связанные с жизнедеятельностью живых организмов, в той или иной степени связаны с теми же золотыми числами, что и обусловливает все более интенсивное изучение этих связей, но, как это ни странно, не свойств и геометрии самих чисел. А они настолько удивительны, что следовало бы поподробнее познакомиться с ними. Один из элементов этих свойств — образование золотого прямоугольного треугольника. Об этом наше изложение.
Прежде всего рассмотрим, что же дает нам деление отрезка в крайнем и среднем отношениях (рис.7). Отмечу, что в постановке задачи говорится о делении одного отрезка на две неравные части а и с так, чтобы весь отрезок (а + с) относился к большей части с, как часть с к меньшей части а. Запишем это отношение:
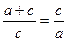 (1)
(1)
Пропорция (1) носит название золотой пропорции.

Рис.7. Деление отрезка в крайнем и среднем отношении.
Отметим, что в данном случае подразумевается конечная в рациональных числах длина отрезка (а + с), кратная некоторому измерительному инструменту. В условии задачи не говорится о невозможности его целочисленного или дробного рационального деления и о нерациональности двух (?) образующихся при делении отрезков.
Это очень важная оговорка. Она подтверждает не преднамеренный, а как бы вероятностный или даже случайный характер деления. Проверим эту случайность. Решим (1), заменив отношение с:а на b:
| b = с:а. | (2) |
Подставим (2) в (1), получим квадратное уравнение:
| b2-b-1=0, | (3) |
решая которое, находим величину b:
| b1 = (1 + √5)/2 = Ф = 1,61...; | (4) |
| b2 = (1- √5)/2 = - 1/Ф = - 0,61... |
РУССКАЯ МАТРИЦА
Поскольку все возрастающие вправо в знаменатель Ф числа диагонали матрицы 4 в своей последовательности аналогичны числам египетской золотой пропорции, включающей условно базисную 1, то можно ожидать, что это условно базисное число является некоторым центром матрицы, построенной по правилам пропорционирования древнерусских саженей. Поставим в центр построения базисную 1 и рассмотрим структуру образовавшейся матрицы 5.
Матрицы 3 и 5 по структуре принципиально одинаковы. Но матрица 5 в качестве отличия имеет центральную базисную 1, которая и становится основой всего числового поля. Все особенности, относящиеся к матрице 3, присущи и матрице 4. Наличие базисной единицы образует ведущую диагональ слева направо снизу вверх, состоящую из чисел египетского ряда. Поэтому данная диагональ может быть названа образующей или главной диагональю. Два числа этой диагонали 1 и Ф не изменяются и определяют числовую структуру всей бесконечной матрицы. Количественное значение числового поля матрицы формируется числом-знаменателем п=2, стоящим в столбце над базисной единицей 1, Знание этих трех чисел и обусловливает возможность формирования бесчисленного количества матриц со свойствами золотых пропорций. Все числа этих матриц, кроме столбца, включающего базисную 1, иррациональны и по своей числовой величине индивидуальны. Вертикальный столбец, или основной ряд с базисной 1, может состоять как из рациональных, так и из иррациональных чисел. В этом столбце строчку над 1 не может занимать только число Ф, ибо тогда вся матрица вырождается в египетский ряд.
Матрица 5
| 913,0 | 738,6 | 697,6 | 483,4 | 391,2 | 316,4 | 207,1 | 167,6 | 135,6 | |||||
| 862,0 | 697,5 | 564,3 | 456,5 | 369,3 | 298,8 | 241,7 | 195,6 | 158,2 | 103,5 | 83,77 | 67,78 | ||
| 532,8 | 431,0 | 348,7 | 282,1 | 228,3 | 184,7 | 149,4 | 120,9 | 98,78 | 79,11 | 51,77 | 41,89 | 33,89 | |
| 266,4 | 215,5 | 174,4 | 141,0 | 114,1 | 92,34 | 74,7 | 60,43 | 48,89 | 39,55 | 25,89 | 20,94 | 16,94 | |
| 133,2 | 107,7 | 87,19 | 70,54 | 57,06 | 46,17 | 37,35 | 30,22 | 24,44 | 19,78 | 12,94 | 10,47 | 8,472 | |
| 66,61 | 53,88 | 43,59 | 35,27 | 28,53 | 23,08 | 18,67 | 15,11 | 12,22 | 9,888 | 6,472 | 5,236 | 4,236 | |
| 33,30 | 26,94 | 21,80 | 17,63 | 14,27 | 11,54 | 9,337 | 7,554 | 6,111 | 4,944 | 3,236 | 2,618 | 2,118 | |
| 16,65 | 13,47 | 10,90 | 8,817 | 7,133 | 5,771 | 4,669 | 3,777 | 3,056 | 2,472 | 1,618 | 1,309 | 1,059 | |
| 8,326 | 6,736 | 5,449 | 4,408 | 3,567 | 2,885 | 2,334 | 1,888 | l,528 | 1,236 | 1,00 | 0,8090 | 0,6545 | 0,5295 |
| 4,163 | 3,368 | 2,725 | 2,204 | 1,783 | 1,443 | 1,167 | 0,9443 | 0,7639 | 0,6180 | 0,50 | 0,4045 | 0,3272 | 0,2647 |
| 2,081 | 1,684 | 1,362 | 1,102 | 0,8916 | 0,721 | 0,5836 | 0,4721 | 0,3820 | 0,3090 | 0,25 | 0,2022 | 0,1636 | 0,1324 |
| 1,041 | 0,8419 | 0,6811 | 0,5511 | 0,4458 | 0,3607 | 0,2918 | 0,2361 | 0,1910 | 0,1545 | 0,125 | 0,1011 | 0,0818 | 0,0662 |
| 0,5203 | 0,4210 | 0,3406 | 0,2755 | 0,2229 | 0,1803 | 0,1459 | 0,1180 | 0,0955 | 0,0772 | 0,0625 | 0,506 | 0,0409 | 0,0331 |
| 0,2602 | 0,2105 | 0,1703 | 0,1378 | 0,1114 | 0,0902 | 0,0729 | 0,0590 | 0,0477 | 0,0386 | 0,0312 | 0,0253 | 0,0204 | 0,0165 |
| 0,1301 | 0,1052 | 0,0851 | 0,0689 | 0,0557 | 0,0451 | 0,0365 | 0,0295 | 0,0239 | 0,0193 | 0,0156 | 0,0126 | 0,0102 | 0,0083 |
| 0,0650 | 0,0526 | 0,0426 | 0,0344 | 0,0279 | 0,0225 | 0,0182 | 0,0147 | 0,0119 | 0,0096 | 0,0078 | 0,0063 | 0,0051 | 0,0041 |
| 0,0325 | 0,0263 | 0,0213 | 0,0172 | 0,0139 | 0,0113 | 0,0091 | 0,0074 | 0,0060 | 0,0048 | 0,0039 | 0,0032 | 0,0026 | 0,0021 |
| 0,0163 | 0,0131 | 0,0106 | 0,0086 | 0,0069 | 0,0056 | 0,0045 | 0,0037 | 0,0030 | 0,0024 | 0,0019 | 0,0016 | 0,0013 | 0,0010 |
| 0,0081 | 0,0066 | 0,0053 | 0,0043 | 0,0035 | 0,0028 | 0,0023 | 0,0018 | 0,0015 | 0,0012 | 0,0010 | 0,008 | 0,006 | 0,0005 |
Матрица 5 имеет ярко выраженную двойную крестовую структуру расположения чисел с центром в базисной 1. Каждое из направлений креста содержит свой коэффициент пропорциональности — знаменатель: главная диагональ — Ф = 1,615..., основной базисный ряд — 2,0, перпендикулярная диагональ — 2,472... и базисная строка — 1,236... С изменением формирующего числа меняются все знаменатели, кроме Ф. Нельзя не отметить, что символика двойного креста используется многими государственными и религиозными структурами.
Крестовая форма, образуемая базисной строкой и столбцом матрицы, обусловливает возможность использовать их как координатную систему для нахождения места любого числа ее множества либо по системе чисел на строке и столбце, либо по показателю степени при знаменателе строки или столбца.
Все числа матрицы взаимосвязаны и создают систему взаимного пропорционирования, но каждое число — единственное, самотождественное и не равное никакому другому числу образование. Строго по другую сторону базисной 1 оно имеет свой обратный аналог, Поэтому прямая, проведенная через 1 и любое число, образует как бы диагональ с числами, кратными ближайшему к 1 числу-знаменателю. А это дает возможность построения матрицы в бесцифровой символической форме. Да и сама матрица, по-видимому, послужила основой эзотерических знаний многих народов.
Строение матрицы 5, многовариантное пропорционирование и бесчисленность ее степенных диагоналей, способных выполнять функции координат или тригонометрических функций, числовое поле, включающее качественные зависимости физических свойств, взаимосвязь всех чисел поля показывают, что матрица отображает актуальную структуру динамической геометрии [9], а ее члены являются коэффициентами золотых пропорций.
Матрица 5 многовариантного пропорционирования, построенная на основе условно базисной 1, золотого числа Ф и с использованием принципа последовательного уменьшения древнерусских саженей в 2 раза, может быть названа русской матрицей.
Трудно предположить, что столь сложная и необычная, даже для нашего времени электронной математики, матрица была разработана каким-либо народом древности только для получения «странных» измерительных инструментов. Но нельзя исключить стороннее привнесение не матрицы, а эталонов длины и методологии их применения. А потому возникает вопрос: имеются ли хоть какие-то аналоги данной матрицы в математической культуре других древних народов?
Сейчас на этот вопрос можно ответить положительно, поскольку аналог русской матрицы в зашифрованном виде отыскался, и записана эта матрица на деревянных панелях, извлеченных из гробницы древнеегипетского зодчего Хеси-Ра, жившего в период правления фараона Джосера (XXVII век до н.э.). Деревянные доски-панели были покрыты с одной стороны великолепной резьбой, а с другой — едва различимыми геометрическими схемами (фотографии резьбы были опубликованы, схемы же так, по-видимому, и не появились в открытой печати).
Изучая геометрию фигур, вырезанных на панелях, архитектор И.Ш. Шевелев обратил внимание на то, что на одной из панелей зодчий держит в руках жезлы, соотносящиеся между собой как 1 : √5, и высказал интуитивное предположение, что это отношение свидетельствует о знании архитектором Хеси-Ра закономерностей золотого сечения. Современная наука достаточно уверенно отвергает возможность знания строителями древнейшего Египта золотых пропорций и умения пользоваться его законами, не отрицая возможности интуитивного использования этих соотношений. Требовались более серьезные доказательства достоверности применения в геометрии фигур на панелях золотых пропорций.
Архитектор И.П.Шмелев [8] провел тщательное изучение геометрической пропорциональности фигур и композиционного строя панелей и на взаимосвязанном числовом материале показал, что жрецы Древнего Египта задолго до кратоновской школы Пифагора владели теорией гармонии, связанной с золотыми пропорциями. Однако, какая конкретно математическая структура зашифрована на панелях, оставалось неясно.
Теперь понятно, что на панелях Хеси-Ра зашифрована математическая конструкция, подобная по своей структуре русской матрице. Часть чисел, найденных И.П. Шмелевым, с точностью до последнего знака входят в матрицу 5, образуя как бы скелет, по которому уже несложно достроить и всю матрицу (в матрице 5 эти числа выписаны из панелей жирным шрифтом). А это означает, что русская матрица 5 и канон Хеси-Ра, зашифрованный на деревянных панелях, образуют одну и ту же математическую структуру (ниже элементы саженей, отображенные на панелях Хеси-Ра, будут рассмотрены подробнее). И можно предположить, что система древнерусских саженей и древнеегипетский канон обязаны своим происхождением одному и тому же источнику, вполне возможно, не имеющему ни Египет, ни Древнюю Русь своей родиной.
Дело в том, что пропорция, образуемая величинами древнерусских саженей, отображенная матрицей А.А. Пилецкого, не вписывается ни в одну, обозримую до 12-13 знака, область матрицы 5. И если бы численные размеры саженей брались из матрицы 5, то их не надо было бы искать. Уже в строке 4 от базисной единицы вверх, где 24 = 16, десятый столбец слева начинается и состоит из чисел, близких величинам саженей, заканчиваясь числом 28 = 256:
| 256. | ||||
| 241,7; 195,6; 158,2; | ||||
| 228,3;184,7; 149,4; | ||||
| 215,5; 174,4; 141,1; | ||||
| 133,2. |
Однако эти величины саженей по неизвестной причине были проигнорированы. Был проигнорирован и другой ряд, начинающийся третьим числом строки 28 = 256:
| 260,5. | ||||
| 246,0; 199,0; 161,0; | ||||
| 232,3; 187,9; 152,0; | ||||
| 219,3; 177,4; 143,6; | ||||
| 135,6 |
который также мог бы служить основой размеров для саженей.
Можно было бы, наконец, сложить попарно близкие размеры и, разделив на 2, получить с точностью до 2 мм величину всех русских саженей. Например, (133,2 + 135,6)/2 = 134,4 и т.д. Но размеры саженей были найдены другим, более сложным способом.
Как уже упоминалось, матрица А.А. Пилецкого не имеет своим началом базисную 1 и не вписывается в числовое поле матрицы 5. Имеет она и еще одну труднообъяснимую особенность. При делении чисел из четырех значащих цифр одних саженей на другие получаем в результате число Ф с фантастической точностью — от 4 до 8 значащих цифр (в приведенных выше двух строках возможных типоразмеров саженей только в трех случаях точность достигает пятого знака). Такие результаты не могут быть случайными, подгонка невозможна уже потому, что по четырем значащим числам точно получается не более четырех цифр. Их можно выявить на значительном цифровом материале только с использованием ЭВМ (трудно вообразить, что в Древнем Египте или в Древней Руси располагали ЭВМ).
Отсутствие базисной единицы 1 в матрице А.А. Пилецкого свидетельствует о том, что шаг значимых чисел русской матрицы по вертикали определяется не знаменателем 2, а другим числом, возведение которого в некоторую степень имеет результатом 2. А это добавляет матрице дополнительные строки «промежуточных» чисел и обеспечивает возможность «сплочения» значимых чисел в одну строку. Следовательно, для нахождения места значимых чисел и матрицы, в которую они входят, необходимо определить число, задающее шаг базисного столбца. И это число, по логике, должно было находиться среди тех чисел, которым в древности придавали сакральное значение. Например 3, 7, 9, 12 и т.д. Поскольку гармоничность является одним из свойств золотого сечения, а число 2 — октава темперированной музыкальной гаммы и образуется малыми секундами, то было сделано предположение, что малая секунда, равная 12√2 = 1,05946... , является шагом по вертикали русской матрицы и обеспечивает ей музыкальную гармоничную структуру. С шагом 1,0594... и был построен новый вариант русской матрицы 6, часть числового поля которой приводится ниже. В ней выделены числовые ряды, входящие и в матрицу 5.
Матрица 6
| 0,1670 | 0,2550 | 0,3895 | 0,5949 | 0,9085 | 1,387 | 2,119 | 3,236 | 4,942 |
| 0,1576 | 0,2407 | 0,3676 | 0,5615 | 0,8575 | 1,309 | 2,000 | 3,054 | 4,665 |
| 0,1488 | 0,2272 | 0,3470 | 0,5300 | 0,8094 | 1,236 | 1,888 | 2,883 | 4,403 |
| 0,1404 | 0,2145 | 0,3275 | 0,5002 | 0,7639 | 1,167 | 1,782 | 2,721 | 4,156 |
| 0,1325 | 0,2024 | 0,3091 | 0,4721 | 0,7211 | 1,101 | 1,682 | 2,568 | 3,923 |
| 0,1251 | 0,1911 | 0,2918 | 0,4456 | 0,6806 | 1,039 | 1,587 | 2,424 | 3,703 |
| 0,1181 | 0,1804 | 0,2754 | 0,4206 | 0,6424 | 0,981 | 1,498 | 2,288 | 3,495 |
| 0,1114 | 0,1702 | 0,2599 | 0,3970 | 0,6063 | 0,926 | 1,414 | 2,160 | 3,298 |
| 0,1052 | 0,1607 | 0,2454 | 0,3747 | 0,5723 | 0,874 | 1,335 | 2,039 | 3,113 |
| 0,0993 | 0,1516 | 0,2316 | 0,3537 | 0,5402 | 0,825 | 1,260 | 1,924 | 2,939 |
| 0,0937 | 0,1431 | 0,2186 | 0,3339 | 0,5099 | 0,779 | 1,189 | 1,816 | 2,774 |
| 0,0885 | 0,1351 | 0,2063 | 0,3151 | 0,4812 | 0,735 | 1,122 | 1,714 | 2,618 |
| 0,0835 | 0,1948 | 0,2974 | 0,4542 | 0,694 | 1,059 | 1,618 | 2,471 | |
| 0,0788 | 0,1204 | 0,1838 | 0,2807 | 0,4287 | 0,655 | 1,000 | 1,527 | 2,332 |
| 0,0744 | 0,1136 | 0,1735 | 0,2650 | 0,4047 | 0,618 | 0,944 | 1,441 | 2,201 |
Построение матрицы 6 начинается с определения шага горизонтального ряда делением Ф на 1,05946... Он оказывается равным 1,52722... Изменение знаменателя вертикального столбца с 2 на 1,05946... вызывает поворот нарастания численных величин по часовой стрелке относительно базисного числа и главной диагонали. И, следовательно, последовательность числовых величин саженей может быть найдена в правой нижней части матрицы 5. Для определения места чисел 134,5; 217,6 ... достаточно последовательно делить их на коэффициент 1,52722... до тех пор, пока частное от деления не окажется равным одному из чисел нисходящего базисного столбца. Поэтому числа данного ряда должны быть вычислены сразу же после нахождения числа 1,05946..., и для нисходящего базисного ряда будут степенью числа 0,94387... Одновременно показатель степени при числе 0,94387... становится номером той строки, на которой находится значимое число (например, 134,5; 217,6...). Число же операций последовательного деления данного значимого числа на 1,5272... является степенью последнего и как бы превращается в номер столбца, в котором находится значимое число.
Проведя соответствующие расчеты, получаем, что число 134,5 находится вправо от базисного столбца на пересечении 60-го столбца с 355-й строкой, а предпоследнее 159,7 — на пересечении 69-го столбца с 418-й строкой. Число 258,4 занимает 417-ю строку 70-го столбца. В матрице, построенной с опорой на крайние значащие числа, очень много чисел, отличающихся от значащих на 1-2 единицы в последнем знаке, их немало встречается и на всем числовом поле от базисной единицы 1. Но все их соотношения не образуют системы, обеспечивающей получение хотя бы трех Ф с точностью до 5 знака. И, по-видимому, отношение 258,4 : 159,7, дающее точность до 8 знака, — ближайшее к центру матрицы. Это еще раз подтверждает преднамеренность в подборе эталонов длины древнерусских саженей.
Вычленим для наглядности из матрицы 6 числовые модули Древнерусских саженей с образуемыми ими числовыми столбцами и рассмотрим возникшую структуру (матрица 7).
Матрица 7
| СТОЛБЦЫ | |||||||||||
| СТРОКИ | |||||||||||
| 142,46 | 217,56 | ||||||||||
| 134,46 | 205,35 | ||||||||||
| 193,83 | |||||||||||
| 182,95 | |||||||||||
| 172,68 | |||||||||||
| 162,99 | |||||||||||
| 153,84 | |||||||||||
| 145,20 | |||||||||||
| 137,05 | |||||||||||
| 129,36 | |||||||||||
| 122,10 | 284,79 | ||||||||||
| 115,25 | 176,01 | ||||||||||
| 166,13 | |||||||||||
| 156,81 | |||||||||||
| 148,01 | |||||||||||
| 139,70 | |||||||||||
| 131,86 | |||||||||||
| 124,46 | |||||||||||
| 117,47 | |||||||||||
| 110,88 | |||||||||||
| 104,66 | |||||||||||
| 98,79 | 230,40 | ||||||||||
| 93,24 | 142,40 | ||||||||||
| 134,40 | |||||||||||
| 126,86 | |||||||||||
| 119,74 | |||||||||||
| 113,02 | |||||||||||
| 106,68 | |||||||||||
| 100,69 | |||||||||||
| 95,04 | |||||||||||
| 89,70 | |||||||||||
| 84,67 | |||||||||||
| 79,92 | 122,05 | 186,4 | |||||||||
| 175,94 | |||||||||||
| 166,06 | |||||||||||
| 156,74 | |||||||||||
| 147,94 | |||||||||||
| 139,64 | |||||||||||
| 131,80 | |||||||||||
| 124,41 | |||||||||||
| 117,42 | |||||||||||
| 110,83 | |||||||||||
| 104,61 | 244,00 | ||||||||||
| 98,74 | 150,80 | 230,30 | |||||||||
| 142,34 | 217,38 | ||||||||||
| 205,18 | |||||||||||
| 193,66 | |||||||||||
| 182,79 | |||||||||||
| 172,53 | |||||||||||
| 162,85 | |||||||||||
| 153,71 | |||||||||||
| 145,08 | |||||||||||
| 136,94 | |||||||||||
| 129,25 | 197,40 | 301,47 | |||||||||
| 284,56 | |||||||||||
| 268,59 | |||||||||||
| 253,51 | |||||||||||
| 239,28 | |||||||||||
| 225,85 | |||||||||||
| 213,18 | |||||||||||
| 201,21 | |||||||||||
| 189,92 | |||||||||||
| 179,26 | |||||||||||
| 169,20 | 258,40 | ||||||||||
| 159,70 | 243,90 | ||||||||||
| 150,74 | 230,21 | ||||||||||
| 142,28 | 217,29 | ||||||||||
| 205,09 | |||||||||||
| и т.д. |
Первое, что обращает на себя внимание в матрице 7, это ступенчатая последовательность расположения значащих чисел. Именно она посредством 12 операций последовательного умножения на 1,05946... обеспечивает удвоение каждого числа.
С другой стороны, от строки с одним значащим числом до строки с другим укладывается 10 промежуточных чисел, и данное значащее число становится 11-м числом, священным (как и 12) в Древнем Египте, имеющим большую социальную значимость (например: территория Древнего Египта делилась на две части — северную и южную — по 11 провинций каждая; число иерофантов в Таро (эзотерическое учение — А.Ч.) состояло из 22 человек; 11 арканов повторены дважды и т.д.).
В матрице 7 при «свертывании» десяти «промежуточных» чисел и выходе 11-го числа на одну строку, например, чисел 176,0 и 142,4 на строку 354, в ней над первым значащим числом находится число 142,46, практически равное располагаемому двумя клетками правее от него числу 142,4. И строка, образованная из трех значащих чисел, как бы замыкает два столбца «промежуточных»чисел, символизируя некоторый оборот или новый возврат к старому. Эта операция «свертывания» «промежуточных» чисел и «подтягивания» в одну строку последующих значащих чисел, т.е. их сопряжение, не меняя структуры матрицы, меняет ее числовое поле, а следовательно, и ранг чисел, превращая их из как бы «соподчиненных» в смежные. Матрица 3 становится некоторым образом совмещенной с матрицей 7, поскольку ее числовое поле входит составной частью в структуру матрицы 7.
Однако изменение структуры матрицы после числового «свертывания» не меняет значимости чисел, «передвинувшихся» со своего «места» к уровню «сопряжения». И они как бы «помнят» о нем и о своей «первоначальной» значимости, какое бы место среди других чисел матрицы они ни занимали.
Это свойство «памяти» числовыми величинами саженей своего прежнего места в матрице среди других чисел и становится основой пропорционирования по золотому сечению, основой качеств, придаваемых саженям иррациональными модулями. Поэтому близкие по длине иррациональные числа русской матрицы, например 217,56 и 230,40 или 150,8 и 159,7 и т.д., не имеющие между собой, на наш взгляд, никакого качественного
различия, занимая в матрице 6 места, разделенные 20-ю рядами, становятся качественно отличными друг от друга. Для них закон качественного равенства всех чисел натурального ряда друг к другу неприменим. Это качественно разные числа, и разность их проявляется физически не только в процессе проведения разбивки зданий и сооружений, но и в виде качественных коэффициентов, обусловливающих взаимосвязи всех свойств тел, коэффициентов, определяющих структуру физических уравнений. Именно отображение природных зависимостей свойствами мер, числами русской матрицы и сообщает всем натуральным естественным отрезкам иррациональную, индивидуальную метрику.
Необъяснимые совпадения структурных элементов матрицы 7 и численных форм древнеегипетской социологии позволяют предположить, что жречество Египта знало о существовании совмещенных матриц и качественном отличии иррациональных чисел, но знания эти были настолько эзотеричны, настолько засекречены, что информация о них в открытой форме не просочилась ни в какие известные на сегодня памятники древней культуры. А панели Хеси-Ра, изучение которых настоятельно следует продолжить, по-видимому, содержат сведения только о матрице 5. Естественно, что сведения о матрицах не входили в программу всех 22 арканов. Об этом свидетельствует то, что Пифагор успешно прошел весь курс арканов и не получил никакого представления об иррациональных числах. Поэтому открытие их в кратонской школе привело в замешательство и его, и его учеников.
Можно предположить, что некоторые элементы матрицы 5 и, в частности, последовательность чисел базисного столбца присутствуют, по-видимому, во всех эзотерических учениях. В таблице 4 для примера приводится последовательность чисел базисного столбца матрицы 5 и числовая прогрессия майянской гармонической системы счисления [22], единственная использующая в качестве основания число 2, умноженное на 10.
Таблица 4
| a | б | ||
| 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = 2 = | 4 096 000 000 000 000 204 800 000 000 000 10 240 000 000 000 512 000 000 000 2 560 000 000 1 280 000 000 64 000 000 3 200 000 16000 8000 400 20 1 | ||
Сделаем небольшое отступление.
Русская матрица является структурой диагональных чисел геометрической прогрессии, и числа каждого диагонального ряда в совокупности подчиняются законам этой прогрессии. Однако если вместо каждого числа оставить только показатель степени, убрав его основание, то получим матрицу уже не геометрической, а арифметической прогрессии. И новые числа по диагоналям этой матрицы обладают всеми свойствами арифметической прогрессии. Изменение статуса матрицы сопровождается и изменением ранга базисного числа — оно становится равным 0 и «плавающим» по главной диагонали, которая в этом случае состоит из одних нулей. Нулевая диагональ разделяет положительную и отрицательную части матрицы. Симметричное числовое поле арифметической матрицы может образовываться как целыми, так и дробными натуральными числами (матрица 8) или формироваться как асимметричное поле (матрица 9). В последнем случае нулевая диагональ становится мнимой, и отрицательное числовое поле матрицы отличается от положительного.
| Матрица 8 | Матрица 9 | |||||||||||||||||
| -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | -22 | -19 | -16 | -13 | -10 | -7 | -4 | -1 | ||
| -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | -19 | -16 | -13 | -10 | -7 | -4 | -1 | ||||
| -1 | -6 | -5 | -4 | -3 | -2 | -1 | -16 | -13 | -10 | -7 | -4 | -1 | ||||||
| -6 | -5 | -4 | -3 | -2 | -1 | -13 | -10 | -7 | -4 | -1 | ||||||||
| -5 | -4 | -3 | -2 | -1 | -10 | -7 | -4 | -1 | ||||||||||
| -4 | -3 | -2 | -1 | -7 | -4 | -1 | ||||||||||||
| -3 | -2 | -1 | -4 | -1 | ||||||||||||||
| -2 | -1 | -1 | ||||||||||||||||
| -1 | ||||||||||||||||||
Асимметрия числового поля может вызываться «деформацией» численных диагоналей путем сдвига числовых величин относительно друг друга так, что нарушается последовательность чередования чисел по вертикальному и горизонтальному рядам. Именно это свойство и возможность прерывания ряда чисел в любом месте используются при построении различных магических квадратов.
Следует отметить, что структура матрицы 8, по-видимому, была известна в древности и также является эзотерическим наследием некоторых народов. Например, элементы арифметической матрицы встречаются в системе Дао (Китай), а цолькин, священный календарь Майя, полностью построен на основе арифметической матрицы.
Даже беглое рассмотрение структуры матриц 5 и 6 показывает, что их числовые поля, кроме многочисленных и интересных математических зависимостей, похоже, никакой тайной информации не содержат, если не считать таковой качественные изменения значимости чисел, и в неизменной форме вряд ли найдут практическое применение.
Так что же скрывается за структурой данных числовых полей? Какие знания были уничтожены вместе с уничтожением египетского жречества вавилонским царем Камбизом?
Еще раз отметим индивидуальность каждого числа матрицы и взаимосвязь его со всеми остальными числами. Это диагональная многопропорциональность числовых рядов: все они проходят через базисную единицу 1, которая остается неизменной, и потому базисная единица 1 имеет иной ранг, чем все остальные числа. Это степенная последовательность расположения чисел по своим диагоналям, обусловливающая некую их
«соподчиненность». Это некоторая сочлененность строк и столбцов и т.д. Но все эти алгебраические зависимости не способствуют пониманию того, какие операции с матрицами могли бы повлиять, например, на существование государства Египет? Только при такой постановке вопроса возможно объяснение той беспрецедентной тайны, которая окружает эзотерические знания и стремление неизвестных разработчиков самыми различными методами передать эти знание как можно более дальним поколениям людей.
ПОНЯТИЕ О ЖИВЫХ ФИГУРАХ
Информация о том, что числа и геометрические фигуры делятся на живые и неживые, время от времени появляется в разнообразной эзотерической литературе. Общим недостатком этой информации является отсутствие однозначных критериев отличия живых чисел и фигур от аналогичных, но неживых. Какое качество, а может быть, какие качества способны придавать таким абстрактным понятиям, как число и геометрическая фигура, свойства, признаваемые за живыми и неживыми телами, в этих публикациях не сообщается. Но все же за этой информацией скрывается истинность, до по
