Знакоопределённость квадратичной формы. Критерий Сильвестра

До сих пор мы рассматривали «внешнее устройство» форм и пришло время изучить их функциональное назначение. Да, по существу, они работают, как функции. Вернёмся к простенькой линейной форме .

Как отмечалось в начале урока, переменные 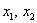могут принимать произвольные действительные значения (мы ограничились ими), и каждой такой паре соответствует определённое значение , например:

, и так далее.

Говоря языком науки, перед нами скалярная функция векторного аргумента, в которой каждому вектору ставится в соответствие определённое число . Обращаю ваше внимание, что сейчас идёт речь не о геометрическом векторе, а о векторе в его алгебраическом понимании.

В зависимости от значений рассматриваемая форма может принимать как положительные, так и отрицательные значения, и то же самое касается любой линейной формы – если хотя бы один из её коэффициентов отличен от нуля, то она может оказаться как положительной, так и отрицательной (в зависимости от значений ).

Такая форма называется знакопеременной. И если с линейной формой всё прозрачно, то с формой квадратичной дела обстоят куда более интересно:

Совершенно понятно, что данная форма может принимать значения любого знака, таким образом, квадратичная форма тоже может быть знакопеременной.

А может и не быть:

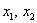– всегда, если только одновременно не равны нулю.

– для любого вектора , кроме нулевого .

И вообще,если для любого ненулевого вектора , , то квадратичную форму называют положительно определённой; если же – то отрицательно определённой.

Также коснёмся «краевых» случаев: если для любого ненулевого вектора , то форма определена неотрицательно, если – то неположительно. У этих форм существует ненулевые векторы 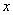, при которых .

Здесь можно привести такой «баян»:

Выделяя полный квадрат, сразу видим неотрицательность формы: , причём, она равна нулю при любом векторе с равными координатами, например: .

«Зеркальный» пример неположительно определённой формы:

И всё бы было хорошо, всё гладко, но определённость квадратичной формы виднА лишь в простых примерах. Как обстоят дела, например, в таком случае:
?

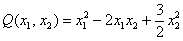Можно предположить, что форма определена положительно, но так ли это на самом деле? Вдруг существуют значения 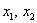, при которых она меньше нуля?

На этот счёт существует теорема: если ВСЕ собственные числа матрицы квадратичной формы положительны*, то она определена положительно. Если все отрицательны – то отрицательно.

* В теории доказано, что все собственные числа действительной симметрической матрицы действительны

Запишем матрицу вышеприведённой формы:
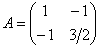и из уравнения найдём её собственные значения:

Решаем старое доброе квадратное уравнение:

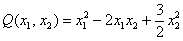, значит, форма определена положительно, т.е. при любых ненулевых значениях 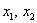она больше нуля.

Рассмотренный метод вроде бы рабочий, но есть одно большое НО. Уже для матрицы «три на три» искать собственные числа – есть занятие долгое и неприятное; с высокой вероятностью получится многочлен 3-й степени с иррациональными корнями.

Как быть? Существует более простой путь!

Критерий Сильвестра

Нет, не Сильвестра Сталлоне :) Сначала напомню, что такое угловые миноры матрицы. Это определители 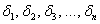которые «разрастаются» из её левого верхнего угла:

и последний из них в точности равен определителю матрицы.

Теперь, собственно, критерий:

1) если ВСЕ угловые миноры матрицы формы больше нуля, то она определена положительно, если они не отрицательны – то неотрицательно.

2) если миноры знакочередуются, причём, первый минор отрицателен, то квадратичная форма является отрицательно определённой. Если нечётные миноры неположительные, а чётные неотрицательные, то форма определена неположительно – осмысливаем, сегодня прямо какой-то день скороговорок :)

Проанализируем угловые миноры матрицы :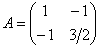

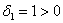, и это сразу говорит нам о том, что форма не определена отрицательно.

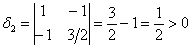
Вывод: все угловые миноры больше нуля, значит, форма 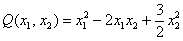определена положительно.

Есть разница с методом собственных чисел? ;)

Запишем матрицу формы 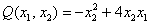из Примера 1:

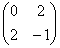
первый её угловой минор 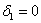, а второй 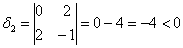, откуда следует, что форма знакопеременна, т.е. в зависимости от значений 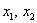, может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.

Возьмём форму 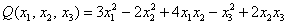и её матрицу из Примера 2:

тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём:
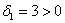, следовательно, форма точно не отрицательна.

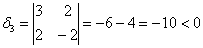, и точно не положительна (т.к. все угловые миноры должны быть положительными).

Вывод: форма знакопеременна.

Теперь разберём более занятную задачку:

Пример 4

Исследовать квадратичную форму на знакоопределенность

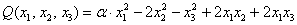
Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем.

Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:

Вычислим угловые миноры:

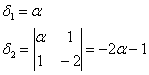
третий определитель я раскрою по 3-й строке:

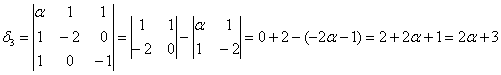
Кстати, в силу симметрии, по 3-му столбцу он раскрывается точно так же.

Дальнейшее решение удобно разбить на 2 пункта:

1) Выясним, существуют ли значения «альфа», при которых форма определена положительно или неотрицательно. Согласно критерию Сильвестра, условию положительности формы соответствует следующая система линейных неравенств:

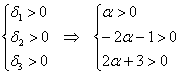
В соответствии с поставленной задачей, сначала разберёмся со 2-м неравенством:

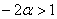
умножим обе его части на 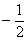, сменив у неравенства знак:
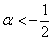, что противоречит первому неравенству системы.

Таким образом, система несовместна, а значит, форма не может быть положительной или неотрицательной ни при каких значениях «альфа».

2) Проведём исследование на отрицательность / неположительнось. Условию отрицательности формы соответствует следующая система линейных неравенств:

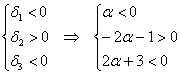
Второе неравенство уже решено: 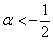, и оно не противоречит первому. И третье неравенство тоже «вписалось в рамки»: .
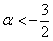Таким образом, имеем совместную систему:

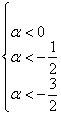
из которой следует, что форма определена отрицательно при 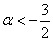. Например, если :
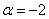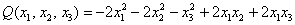– то при любом ненулевом векторе 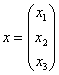данная форма будет строго отрицательна.

Осталось исследовать «пограничный» случай. Если 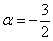, то:

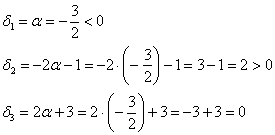
что соответствует критерию неположительности формы.

Иными словами, квадратичная форма 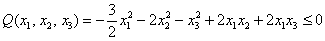, причём, нулю она равна и при некоторых ненулевых значениях .

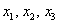Ответ: при 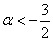форма определена отрицательно, при 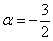неположительно, в остальных случаях форма знакопеременна.

Символическое задание для самостоятельного решения:

Пример 5

Исследовать квадратичные формы на знакоопределенность

а)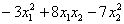

б)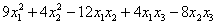

Решение и ответ рядом, после чего я жду вас на следующем уроке – о каноническом виде квадратичной формы.

Как привести квадратичную форму к каноническому виду?
Метод Лагранжа

Приветствую вас на втором уроке о квадратичных формах, который посвящен её каноническому виду и соответствующим методам. «Чайникам» и вновь прибывшим с поисковика рекомендую сначала ознакомиться первой частью – чтобы быстренько привести себя в форму :)

И мы сразу же продолжаем. Если в квадратичной форме отсутствуют слагаемые с парными произведениями переменных, то говорят, что она находится в каноническом виде. …Первая часть предложения была понятной? Тогда едем дальше.

Любую квадратичную форму можно привести к каноническому виду:

– форму двух переменных – к виду (различаем коэффициенты «а» и «альфа»!);

– трёх переменных – к виду ;

…

– форму переменных «простыня» – к виду:

Чуть позже я сформулирую это утверждение более строго, расскажу о геометрическом смысле, да и просто смысле приведения – после того, как мы освоим техническую сторону вопроса.

И ключевой момент этой технической стороны состоит в линейных заменах:
– ТАКИХ, которые как раз и приводят форму к каноническому виду.

Систему часто записывают в виде компактного матричного уравнения , где:
– столбцы старых и новых переменных, – матрица линейного преобразования.

Внимание! Если вам не понятно, как из уравнения получить систему замен, обязательно посмотрите здесь (после Примера 3). Это важно.

Существует несколько способов приведения формы к каноническому виду, и в рамках сайта я расскажу о методе Лагранжа и методе ортогональных преобразований (уже следующий урок).

Начнём с наиболее простого метода:

Пример 6

Привести квадратичную форму к каноническому виду методом Лагранжа. Записать матрицу соответствующего линейного преобразования.

простенько и со вкусом

Решение: здесь используются стандартные замены с последующим применением бородатой формулы :

– форма в каноническом виде.

Запишем матрицу проведённого линейного преобразования: – она состоит из «игрековых» коэффициентов замен .

Ответ: ,

Пример, конечно, прозрачный, но сразу зададимся вопросом – как выполнить проверку? Её можно выполнить матричным методом по формуле , где – транспонированная матрица линейного преобразования, 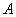– исходная и – новая матрица квадратичной формы.

В нашем случае – исходная матрица формы , и, перемножая три матрицы:

– получаем матрицу формы , что и требовалось проверить.

Но то был лишь частный случай:

Пример 7

Привести квадратичную форму к каноническому виду методом Лагранжа.

Записать матрицу соответствующего линейного преобразования.

Решение: когда в форме присутствуют квадраты переменных (а они есть почти всегда), то используется другой приём. Идея состоит в выделении полных квадратов по формулам , с дальнейшей заменой переменных.

Сначала выбираем какую-нибудь переменную, которая находится в квадрате, здесь можно выбрать или . Переменные традиционно перебирают по порядку, поэтому рассматриваем и собираем вместе все слагаемые, где есть эта переменная:

«двойку» удобно вынести за скобки:

очевидно, всё дело сведётся к формуле , и нам нужно искусственно организовать данную конструкцию. Для этого в скобках прибавляем и, чтобы ничего не изменилось – за скобками проводим вычитание:

выделяем полный квадрат:
, после чего выполним проверку обратными действиями – раскроем скобки и приведём подобные слагаемые:
, ОК

Теперь проведём замены :

– форма в каноническом виде.

И тут вроде бы можно записать матрицу линейного преобразования, но есть одна загвоздка, проведённые замены имеют вид :

но нам-то нужна другая матрица – матрица уравнения .

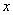Для разрешения уравнения относительно умножим обе его части на слева:

Я не буду подробно расписывать процесс нахождения обратной матрицы, а сразу приведу готовый результат – искомая матрица линейного преобразования. Напоминаю (см. начало урока), что в этой матрице находятся «игрековые» коэффициенты «прямых» замен:

Справка: возможно, ещё не все до конца понимают, как из матричного уравненияполучается система замен. В правой части уравнения выполняем матричное умножение:

Две матрицы равны, если равны их соответствующие элементы, таким образом:

И в самом деле, выполняя прямые замены в форме :

– получаем её канонический вид, найденный выше.

То же самое можно установить матричным методом. Запишем матрицу формы и в результате перемножения трёх матриц:

– получим «каноническую» матрицу.

Прямая подстановка, безусловно, удобнее, но особенность метода Лагранжа состоит в том, что к канонической форме мы подбираемся «с другой стороны» (за исключением немногочисленных случаев наподобие предыдущего примера).

Ответ: ,

Если условие не запрашивает линейное преобразование, то решение заметно сократится. Но мы его наоборот – ещё больше увеличим :) В образовательных целях.

Квадратичную форму можно привести к каноническому виду не единственным способом. Это следует уже из самого алгоритма действий. Так, например, полный квадрат можно выделить без выноса «двойки» за скобку:

контроль:

и, после замен тоже получается канонический, но уже другой вид рассматриваемой формы:

Кстати, начать можно и со 2-й переменной –

выполните это задание самостоятельно:

Привести квадратичную форму к каноническому виду, выделив полный квадрат при переменной . Записать матрицу соответствующего линейного преобразования.

Решение и ответ в конце урока.

Повысим уровень сложности, а точнее, количество переменных:

Пример 8

Привести квадратичную форму к каноническому виду методом Лагранжа

Записать матрицу соответствующего линейного преобразования.

Решать начинаем традиционно – группируем все слагаемые, которые содержат 1-ю переменную:

и начинаем конструировать полный квадрат:

здесь чётко просматривается формула и для её применения мы должны прибавить и вычесть :

«собираем» квадрат суммы и упрощаем «хвост», распишу это упрощение подробно:

контроль:
–ч.т.п.

На следующем шаге обычно выделяется ещё один полный квадрат, но у нас осталось единственно слагаемое с парным произведением, и в подобной ситуации сразу же выполняются замены, в данном случае :

В результате получен неканонический вид формы и поэтому нам потребуется ещё одна замена. Используем стандартный трюк, который встретился в самом начале урока:
. Таким образом, получаем:

– форма в каноническом виде.

Теперь нужно записать матрицу соответствующего линейного преобразования. Ситуация осложнятся тем, что мы провели ДВА преобразования, и нам предстоит найти их композицию – результирующее преобразование, которое выражает 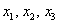через сумму / разность «игреков».

Давайте разбираться, что к чему. Запишем первую замену в матричной форме: .
Вторая же замена имеет несколько другой вид:

Из уравнений следует, что:

Для разрешения полученного уравнения относительно 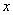умножим обе его части на слева:

Таким образом, нам нужно найти обратную матрицу (уже не нужно:)) и выполнить матричное умножение:

– получив тем самым искомое результирующее преобразование.

Но подставлять в форму что-то неохота, и поэтому «пропустим через мясорубку» её матрицу , благо, матричный калькулятор под рукой:
– получена матрица приведённой формы , в чём мы и хотели убедиться.

Обратите внимание на удобство матричной записи и матричного метода – они практически «сводят на нет» путаницу в индексах и степенях квадратичной формы.

Ответ: ,

Тренируемся:

Пример 9

Привести квадратичную форму к каноническому виду методом Лагранжа

а)

б) – особенно часто встречающийся тип приведения.

В образцах решения использован «традиционный» путь, т.е. полные квадраты выделяются по порядку, начиная с 1-й переменной. Перед заменой переменных полезно выполнять обратный ход – раскрывать скобки и приводить подобные слагаемые, чтобы получить исходный вид. Это вполне надёжный способ проверки. Также обратите внимание, что здесь не требуется указывать линейное преобразование, однако, я коротко рассказал, как его находить (мало ли, понадобится).

…у всех всё получилось? Тогда продолжаем – начинается самое интересное! Наверное, все понимают, что подавляющее большинство линейных преобразований не приводят нас к желаемому результату. Вернёмся к подопытной форме Примера 7 и проведём, например, такую замену: .
Запишем матрицу формы , матрицу преобразования и воспользуемся знакомой формулой:

Таким образом, форма приняла другой, тоже неканонический вид .

И тут я хочу отметить ещё одно преимущество матричного решения, о котором не говорил. В результате умножения ДОЛЖНА получиться симметрическая и только такая матрица, и этот факт значительно снижает риск пропустить ошибку. Но, разумеется, можно выполнить и прямую подстановку в :

Правда, запутаться тут легче и гарантий никаких.

Далее. Все преобразования, которые нам встретились выше, не вырождены. Что это означает? Это означает, что для них существует обратное преобразование – образно говоря, «путь назад». Теперь не образно:) определитель матрицы невырожденноголинейного преобразования непременно отличен от нуля , что гарантирует существование обратной матрицы и «зеркальной» формулы , с помощью которой мы можем однозначно восстановить исходную матрицу .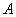

Чего не скажешь о преобразовании вырожденном – это «билет в один конец». Одним из таких преобразований является тривиальное нулевое преобразование. Так, например, если , то форма вырождается в нулевую форму с матрицей . Обратного пути нет, то есть, если нам изначально дана вырожденная «игрековая» форма с матрицей , то невозможно выяснить, от какой формы она произошла.

Существуют и другие типы «вырождения», но всех их объединяет тот факт, что определитель матрицы такого преобразования равен нулю: , из чего следует, что обратной матрицыне существует, а значит, не существует и возврата.

А теперь заметим, что нулевое преобразование привело нас… к каноническому виду ! И в самом деле – это же канонический вид по определению. И поэтому сейчас мы усилим утверждение, сформулированное в начале урока:любую квадратичную форму можно привести к каноническому виду с помощью невырожденного линейного преобразования. Существование такого преобразования, в частности, гарантирует метод Лагранжа.

И сейчас я озвучу кульминационный и ОЧЕНЬ важный момент: невырожденное линейное преобразование не меняет СУЩНОСТИ квадратичной формы. Здесь можно привести такой ассоциативный пример: рассмотрим произвольную ненулевую форму и представим, что это квадратный лист бумаги, на котором записано некое слово. Если форма находится в неканоническом виде, то лист занимает такое положение, в котором мы слова не видим, или же только догадываемся, что это за слово.

1) Невырожденное преобразование, которое приводит форму к каноническому виду, поворачивает листок бумаги к нам «лицом» – чтобы слово было отчётливо видно. Поскольку таких преобразований на самом деле много, то лист бумаги в общем случаебудет менять свой размер и местоположение, и размер шрифта тоже будет меняться. Но что не изменится – так это слово.

2) Невырожденное преобразование, которое НЕ приводит форму к каноническому виду, делает то же самое с большим и толстым нюансом: слова мы по-прежнему не видим.

3) Вырожденное линейное преобразование либо полностью стирает с листа слово (нулевое преобразование), либо стирает отдельные буквы – так, чтобы нельзя было однозначно сказать, от какого слова они остались; причём, мы можем не увидеть даже и этих букв (если форма осталась в неканоническом виде).

И, завершая ассоциацию, отметим наиболее интересный случай – когда невырожденноепреобразование не только приводит форму к каноническому виду, но ещё и сохраняет размер листа, т.е. поворачивает его к нам в неизменном виде. Жду вас на третьем уроке о методе ортогонального преобразования, где мы продолжим увлекательную беседу и вложим в сущность формы конкретный геометрический смысл.

12.Комплексные числа( 3 формы и алгебраические операции)

1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

На любой вкус и цвет – кому, что интересно. А комплексные числа действительно становятся любимой темой,... после того, как студенты знакомятся с другими разделами высшей алгебры =). Если Вы являетесь чайником, или только-только приступили к изучению комплексных чисел, то параграфы лучше прочитать по порядку, без «перескоков».

Сначала «поднимем» информацию об «обычных» школьных числах. В математике они называются множеством действительных чисел и обозначаются буквой (в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.

Понятие комплексного числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.

Если хотите, комплексное число – это двумерное число. Оно имеет вид , где и – действительные числа, – так называемая мнимая единица. Число называется действительной частью ( ) комплексного числа 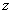, число называется мнимой частью ( ) комплексного числа .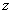

– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:

Как упоминалось выше, буквой принято обозначать множество действительных чисел. Множествожекомплексных чиселпринято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей:
– действительная ось
– мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать масштаб, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:
, ,
, ,
, , ,

По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел является подмножеством множества комплексных чисел .

Числа , , – это комплексные числа с нулевой мнимой частью.

Числа ,