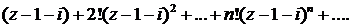Комплексные числа и ряды с комплексными членами
1. Комплексные числа. Комплексными числами называются числа вида х+iy, где х и у -действительные числа, i—мнимая единица, определяемая равенством i2=-1. Действительные числа х и у называются соответственно действительной и мнимой частями комплексного числа z. Для них вводятся обозначения: x=Rеz; y=Imz.
. 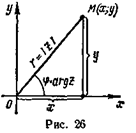
Геометрически каждое комплексное число z=x+iy изображается точкой М (х; у) координатной плоскости xOу (рис. 26). В этом случае плоскость хОу называют комплексной числовой плоскостью, или плoскостью комплексного переменного z.
Полярные координаты r и φ точки М, являющейся изображением комплексного числа z, называются модулем и аргументом комплексного числа z; для них вводятся обозначения: r=|z|, φ=Arg z.
Так как каждой точке плоскости соответствует бесчисленное множество значений полярного угла, отличающихся друг от друга на 2kπ (k—целое положительное или отрицательное число), то Агg z—бесконечнозначная функция z.
То из значений полярного угла φ, которое удовлетворяет неравенству –π < φ ≤ π, называют главным значением аргумента z и обозначают аrg z.
В дальнейшем обозначение φ сохраним только для главного значения аргумента z, т.е. положим φ =аrg z, в силу чего для всех остальных значений аргумента z получим равенство
Аrg z = аrg z + 2kπ =φ + 2kπ.
Соотношения между модулем и аргументом комплексного числа z и его действительной и мнимой частями устанавливаются формулами
x = r cos φ; y = r sin φ.
Отсюда
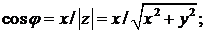
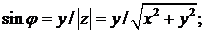
Аргумент z можно определить также по формуле
arg z = аrctg (у/х)+С,
где С = 0 при х > 0, С = +π при х<0, у > 0; С = — π при x < 0, у < 0.
Заменяя x и у в записи комплексного числа z = х+iу их выражениями через r и φ, получаем так называемую тригонометрическую форму комплексного числа:
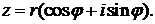
Комплексные числа z1 = х1 + iy1 и z2 = x2 + iy2 считаются равными тогда и только тогда, когда у них равны по отдельности действительные и мнимые части:
z1 = z2, если x1 = x2, у1 = у2.
Для чисел, заданных в тригонометрической форме, равенство имеет место, если модули этих чисел равны, а аргументы отличаются на целое кратное 2π:
z1 = z2, если |z1| = |z2| и Аrg z1 = Аrg z2+2kπ.
Два комплексных числа z = х+iу и z = х —iу с равными действительными и противоположными мнимыми частями называются сопряженными. Для сопряженных комплексных чисел выполняются соотношения
|z1| = |z2|; аrg z1 = —аrg z2,
(последнему равенству можно придать вид Аrg z1+Аrg z2 = 2kπ).
Действия над комплексными числами определяются следующими правилами.
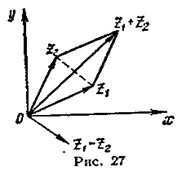
Сложение. Если z1 = x1 + iy1, z2=x2+iy2, то
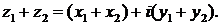
Сложение комплексных чисел подчиняется переместительному и сочетательному законам:
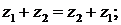
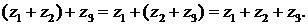
Вычитание. Если z1 = x1 +iy1, z2 = x2 + iy2, то
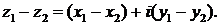
Для геометрического пояснения сложения и вычитания комплексных чисел полезно изображать их не точками на плоскости z, а векторами: число z = х + iу изображается вектором 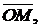 имеющим начало в точке О («нулевой» точке плоскости — начале координат) и конец в точке М (х; у). Тогда сложение и вычитание комплексных чисел выполняется по правилу сложения и вычитания векторов (рис. 27).
имеющим начало в точке О («нулевой» точке плоскости — начале координат) и конец в точке М (х; у). Тогда сложение и вычитание комплексных чисел выполняется по правилу сложения и вычитания векторов (рис. 27).
Такое геометрическое истолкование операций сложения и вычитания векторов позволяет легко установить теоремы о модуле суммы и разности двух и сумме нескольких комплексных чисел, выражаемые неравенствами:
| |z1|-|z2| | ≤ |z1±z2| ≤ |z1| + |z2| ,
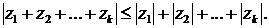
Кроме того, полезно помнить, что модуль разности двух комплексных чисел z1 и z2 равен, расстоянию между точками, являющимися их изображениями на плоскости z:| |z1-z2|=d(z1,z2) .
Умножение. Если z1 = x1 +iy1, z2 = x2 + iy2. то
z1z2=(x1x2-y1y2)+i(x1y2+x2y1).
Таким образом, комплексные числа перемножаются как двучлены, причем i2 заменяется на —1.
ЕСЛИ 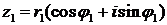 ,
, 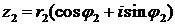 , то
, то
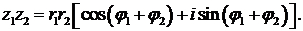
Таким образом, модуль произведения равен произведению модулей сомноэки* телей, а аргумент произведения—сумме аргументов сомножителей. Умножение комплексных чисел подчиняется переместительнЬму, сочетательному и распределительному (по отношению к сложению) законам:
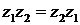 ;
; 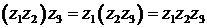 ;
; 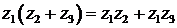 .
.
Деление. Для нахождения частного двух комплексных чисел, заданных в алгебраической форме, следует делимое и делитель умножить на число, сопряженное с делителем:
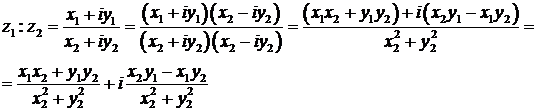
' Если 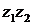 заданы в тригонометрической форме, то
заданы в тригонометрической форме, то
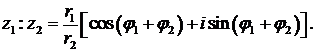
Таким образом, модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.
Возведение в степень. Если z= 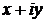 , то по формуле бинома Ньютона имеем
, то по формуле бинома Ньютона имеем
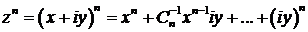
(п—целое положительное число); в полученном выражении надо заменить степени i их значениями:
i2 = -1; i3=i; i4 =1; i5 =1,…
и, в общем случае,
i4k = 1; i4k+1=i; i4k+2 = -1; i4k+3 = -i.
Если 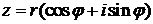 , то
, то
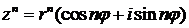
(здесь п может быть как целым положительным, так и целым отрицательным числом).
В частности,
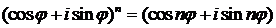
(формула Муавра).
Извлечение корня. Если п—целое положительное число, 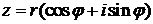 , то корень n-й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
, то корень n-й степени из комплексного числа z имеет n различных значений, которые находятся по формуле
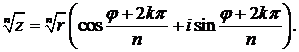
где k=0, 1, 2, ..., n—1.
437.Найти (z1z2)/z3, если z1 = 3 + 5i, z2 = 2 + 3i, z3 = 1+2i.
∆ 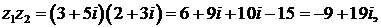
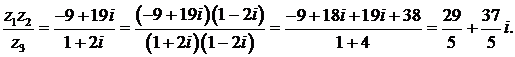 ▲
▲
438. Представить в тригонометрической форме комплексное
число z = 2 + 5i.
∆ Находим модуль комплексного числа: 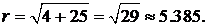 . Находим главное значение аргумента:
. Находим главное значение аргумента: 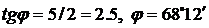 . Следовательно,
. Следовательно, 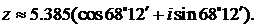 ▲
▲
439.Представить в тригонометрической форме комплексное
число 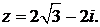
∆ Находим 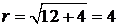 ,
, 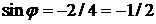 ;
; 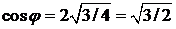 ,
, 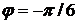 ,т.е.
,т.е.
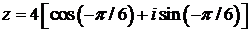 . ▲
. ▲
440.Представить в тригонометрической форме комплексные
числа 1, i, —1, —i.
∆ 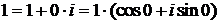
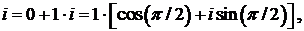
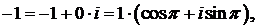
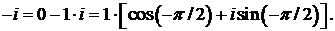 ▲
▲
441.Представить числа 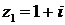 ,
, 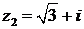 ,
, 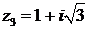
в тригонометрической форме, а затем найти комплексное число
z1/(z2z3).
∆ Находим
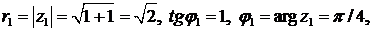
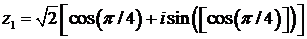 ;
;
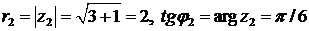 ,
,
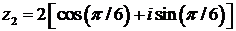 ;
;
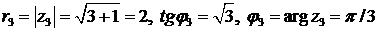 ,
,
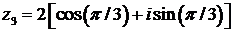 .
.
Следовательно,
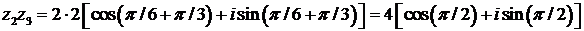
и
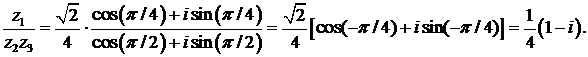 ▲
▲
442.Найти все значения 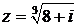 .
.
∆ Запишем комплексное число 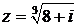 в тригонометрической форме. Имеем
в тригонометрической форме. Имеем 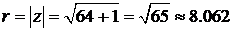 ,
, 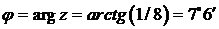 ,
, 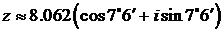 . Следовательно,
. Следовательно,
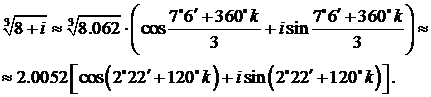
Если 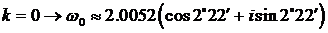 ;
;
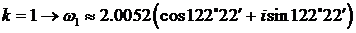 .
.
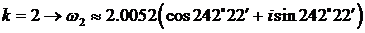
Следовательно, 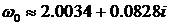 ,
, 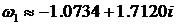 ,
, 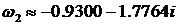
443.Решить двучленное уравнение ω5 + 32i = 0.
∆ Перепишем, уравнение в виде ω5 + 32i = 0. Число —32i представим в тригонометрической форме:
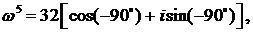 или
или 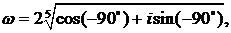
т. е.
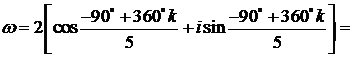
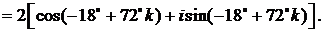
Если k = 0, то 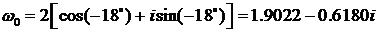 (A).
(A).
k =1, 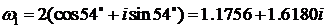 (B).
(B).
k =2, 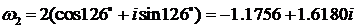 (C).
(C).
k =3, 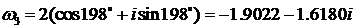 (D).
(D).
k =4, 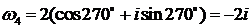 (E).
(E).
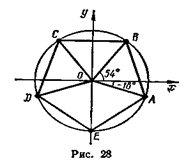
Корням двучленного уравнения соответствуют вершины правильного пятиугольника, вписанного в окружность радиуса R = 2 с центром в начале координат (рис. 28).
Вообще корням двучленного уравнения ωn=а, где а—комплексное число, соответствуют вершины правильного n-угольника, вписанного в окружность с центром в начале координат и радиусом, равным 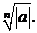 ▲
▲
444.Пользуясь формулой Муавра, выразить соs5φ и sin5 φ через соsφ и sinφ.
∆ Левую часть равенства 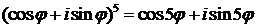 преобразуем по формуле бинома Ньютона:
преобразуем по формуле бинома Ньютона:
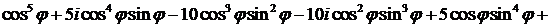
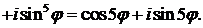
Остается приравнять действительные и мнимые части равенства:
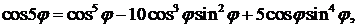
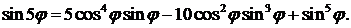 ▲
▲
445.Дано комплексное число z = 2—2i. Найти Re z, Im z, |z|, arg z.
446.Представить в тригонометрической форме комплексное число z = —12 + 5i.
447. Вычислить по формуле Муавра выражение (соs 2° + isin 2°)45.
448. Вычислить по формуле Муавра 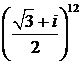 .
.
449.Представить в тригонометрической форме комплексное число
z = 1 + соs 20° +isin 20°.
450.Вычислить выражение (2 + 3i)3.
451.Вычислить выражение 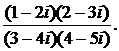
452.Вычислить выражение 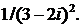
453.Представить в тригонометрической форме комплексное число 5—3i.
454.Представить в тригонометрической форме комплексное число —1 + i.
455.Вычислить выражение 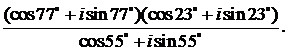
456.Вычислить выражение 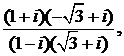 предварительно представив в тригонометрической форме множители в числителе и знаменателе.
предварительно представив в тригонометрической форме множители в числителе и знаменателе.
457.Найти все значения 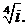
458.Решить двучленное уравнение 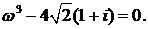
459.Выразить соs4φ и sin4φ через соsφ и sinφ.
460.Показать, что расстояние между точками z1 и z2 равно | z2— z1|.
∆ Имеем z1 = х1 + iу1, z2 = х2 + iу2, z2—z1 = (x2-x1) + i(y2-y1), откуда
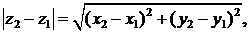
т.е. | z2— z1| равно расстоянию между данными точками. ▲
461.Какая линия описывается точкой z, удовлетворяющей уравнению 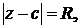 где с—постоянное комплексное число, а R>0?
где с—постоянное комплексное число, а R>0?
462. Каков геометрический смысл неравенств: 1) |z—с|<R;2) |z—с|>R?
463.Каков геометрический смысл неравенств: 1) Re z > 0; 2) Im z < 0?
2. Ряды с комплексными членами. Рассмотрим последовательность комплексных чисел z1, z2, z3, ..., где zп = хп+iуп (п = 1, 2, 3, ...). Постоянное число с = а + bi называется пределом последовательности z1, z2, z3, ..., если для всякого сколь угодно малого числа δ>0 найдется такой номер N, что рее значения zп с номерами п > N удовлетворяют неравенству \zп—с\ < δ . В этом случае пишут 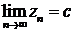 .
.
Необходимое и достаточное условие существования предела последовательности комплексных чисел состоит в следующем: число с=а+bi является пределом последовательности комплексных чисел х1+iу1, х2+iу2, х3+iу3, … тогда и только тогда, когда 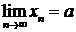 ,
, 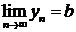 .
.
Ряд
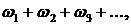 (1)
(1)
членами которого являются комплексные числа, называется сходящимся, если n-я частичная сумма ряда Sn при п → ∞ стремится к определенному конечному пределу. В противном случае ряд (1) называется расходящимся.
Ряд (1) сходится тогда и только тогда, когда сходятся ряды с действительными членами
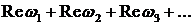 (2)
(2)
и
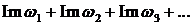 (3)
(3)
Если суммой ряда (2) является число S', а суммой ряда (3) — число S", то суммой ряда (1) служит комплексное число S = S'+iS".
Если ряд
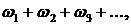 (где
(где 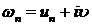 )
)
сходится, то 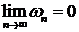 (т.е.
(т.е. 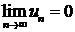 ,
, 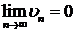 ).
).
Если сходится ряд
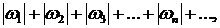
то сходится и ряд
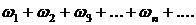
В этом случае последний ряд называется абсолютно сходящимся.
Пусть дан степенной ряд
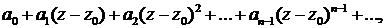
где z0, а0, а1, а2, ...—комплексные числа, причем коэффициенты ряда отличны от нуля, а z—комплексное переменное.
Этот ряд сходится в круге 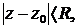 где
где 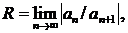 и расходится вне указанного круга, т. е. при значениях г, удовлетворяющих неравенству
и расходится вне указанного круга, т. е. при значениях г, удовлетворяющих неравенству 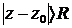
464.Исследовать сходимость ряда
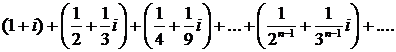
∆ Ряды
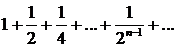 и
и 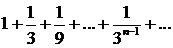
сходятся, так как они составлены из членов бесконечно убывающих геометрических прогрессий. Следовательно, сходится и заданный ряд с комплексными членами.
Найдем суммы этих прогрессий:
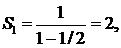
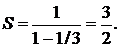
Следовательно, сумма рассматриваемого ряда есть комплексное число 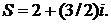 ▲
▲
465.Исследовать сходимость ряда
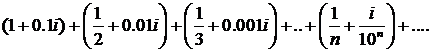
∆ Рассмотрим ряды
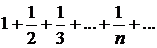 и
и 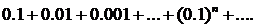
Первый из них расходится, следовательно, расходится и данный ряд с комплексными членами. ▲
466.Исследовать сходимость ряда
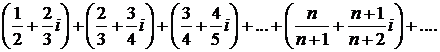
∆ Ряд расходится, так как общий его член 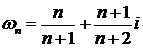 не стремится к нулю (в этом рекомендуем убедиться самостоятельно). ▲
не стремится к нулю (в этом рекомендуем убедиться самостоятельно). ▲
467.Показать, что ряд
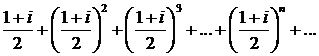
сходится абсолютно.
∆ Так как 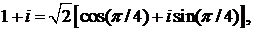 то
то
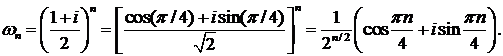
Следовательно, 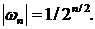 Составим ряд из модулей:
Составим ряд из модулей:
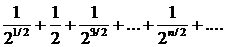
Этот ряд, члены которого образуют бесконечно убывающую геометрическую прогрессию, сходится; следовательно, заданный ряд с комплексными членами сходится абсолютно. ^
468.Найти область сходимости ряда
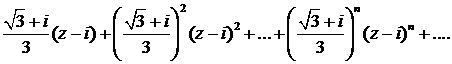
∆ Имеем
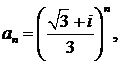
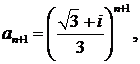
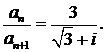
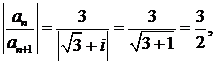
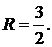
Областью сходимости ряда является круг 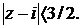
469.Показать, что ряд
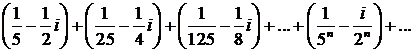
сходится и найти его сумму.
470.Исследовать сходимость ряда
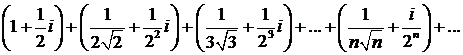
471.Исследовать сходимость ряда с общим членом 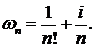
472.Показать, что ряд
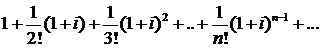
сходится абсолютно.
473.Найти область сходимости ряда
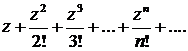
474.Найти область сходимости ряда