Изменения токов ветвей, вызванные приращением сопротивления одной ветви (теорема вариаций)

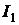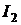Выделим ветви 1 и 2 с токами и (рис. 15.1, а,) заключив остальную часть схемы вместе с источниками энергии в прямоугольник 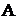(активный); проводимост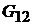и и 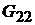полагаем известными. Пусть сопротивление ветви 2

изменилось на 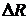(рис 15.1, б), в результате чего токи стали [1, 20]:

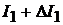и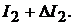

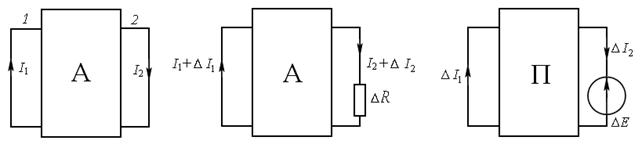
а б в

Рис. 15.1

В соответствии с теоремой компенсации заменим 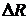на ЭДС:

,

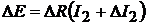направленную встречно току 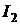. На основании принципа наложения можно сказать, что приращение токов 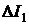и 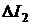вызваны ЭДС 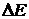в схеме (см. рис.15.1, в), в которой часть схемы, заключённая в прямоугольник, стала пассивной (пря-

моугольник П).

Так как схема внутренних соединений и значения сопротивлений в схеме прямоугольника остались без изменений, то проводимост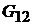и и 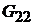в схеме на рис. 15.1, в имеют те же значения, что на рис. 15.1, а. Для схемы на рис. 15.1, в имеем:

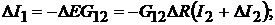
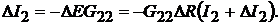
Знаки «−» поставлены потому, что ЭДС 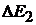направлена встречно току 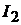. Отсюда

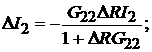
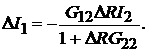(15.1)

Соотношения (15.1) позволяют определить изменение токов в ветвях 1 и 2, вызванные изменением сопротивления в ветви 2.

Пример 29.В схеме (см. рис.15.1) 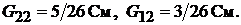Токи 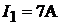, 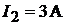. Определить ток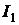и и 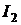после того, как сопротивление ветви 2 возросросло на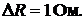

Решение. По формулам (15.1):

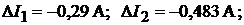
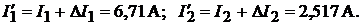
Пример 30.В цепи (рис. 15.2) изменение 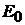на 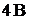приводит к изменению ток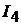а на 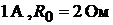. Определить изменение напряжения 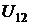при измене-

нии 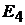на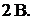

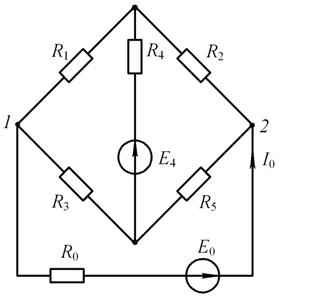
Рис. 15.2

Решение. Решение основано на использовании теоремы о приращениях и по-

нятии о собственных и взаимных проводимостях.

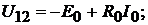
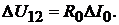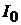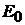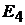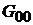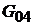Напряжение Ток связан с и с помощью и , где

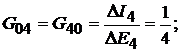
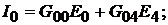
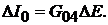
Окончательно,

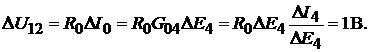
МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

Метод узловых потенциалов позволяет уменьшить число совместно решае-

мых уравнений до 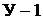, где 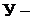число узлов схемы замещения цепи. Метод основан на применении первого закона Кирхгофа и заключается в следую-

щем [3, 6, 8, 11, 13, 15, 17, 20]:

1) один узел цепи принимаем базисным с нулевым потенциалом. Такое до-

пущение не изменяет значения токов в ветвях, так как ток в каждой ветви зави-

сит только от разностей потенциалов узлов, а не от действительных значений

потенциалов;

2) для остальных 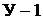узлов составляем уравнение по первому закону Кирхгофа, выражая токи ветвей через потенциалы узлов;

3) решением составленной системы уравнений определяем потенциалы 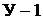узлов относительно базисного, а затем токи ветвей по обобщённому зако-

ну Ома (4.5).

Рассмотрим применение метода на примере расчёта цепи по рис. 16.1, содер-

жащей 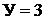узла. Узел 3 принимаем базисным, т.е. 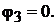Для узлов 1 и 2 уравнения по первому закону Кирхгофа:

узел 1: 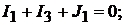узел 2: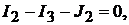

где

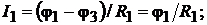
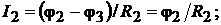
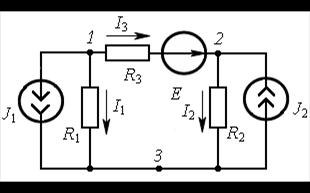
Рис. 16.1

После подстановки

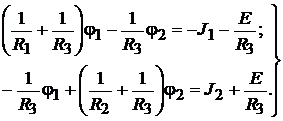(16.1)

Решение системы уравнений (16.1) методом подстановок определяет потен-

циалы узлов 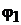и 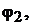а следовательно, и токи ветвей по формуле (4.5).

Из записи (16.1) очевиден принцип составления уравнений по методу узло-

вых потенциалов. В левой части уравнений коэффициент при потенциале рас-

сматриваемого узла положителен и равен сумме проводимостей, сходящихся к нему ветвей; коэффициенты при потенциалах узлов, соединённых ветвями с рассматриваемым узлом, отрицательны и равны проводимостям соответствую-

щих ветвей.

Правая часть уравнений содержит алгебраическую сумму токов ветвей с ис-

точниками токов и токов короткого замыкания ветвей с источниками ЭДС, схо-

дящихся к рассматриваемому узлу, причем слагаемые берутся со знаком плюс (минус), если ток источника тока и ЭДС направлены к рассматриваемому узлу (от узла). Напряжения, создаваемые источниками питания постоянного тока, совпадающие по направлению с направлением напряжения между узлами 1−2 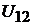, записываются со знаком «+», а несовпадающие с направлением − со знаком «−».

Если схема имеет n узлов, то ей соответствует система из 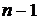уравнений:

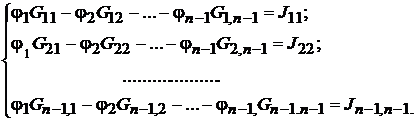(16.2)

В общем случае 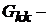сумма проводимостей ветвей, сходящихся в узле ;

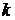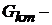сумма проводимостей ветвей, непосредственно соединяющих узлы 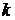и

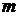. Если между какими-либо двумя узлами ветвь отсутствует, то соответствую-

щая проводимость равна нулю. В формировании узлового тока k-узла 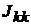участвуют те ветви, подходящие к этому узлу, которые содержат источники ЭДС и (или) тока. Если ЭДС 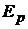p-ветви направлены к k-узлу, то её вклад в формирование 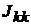равен 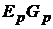, если эта ЭДС направлена от k-узла, то её вклад составляет 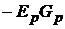. Если к k-узлу притекает ток от источника тока, то он должен быть введён в 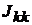со знаком плюс, если этот ток от источника уте-

кает, то он должен входить в 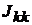со знаком минус. После решения системы (16.2) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС.

Выражение для напряжений между узлами 1 и 2 цепи, изображённой на рис. 16.2, записываем в следующем виде [9]:

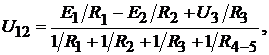
(16.3)

где 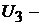напряжние, созданное источником питания постоянного тока.

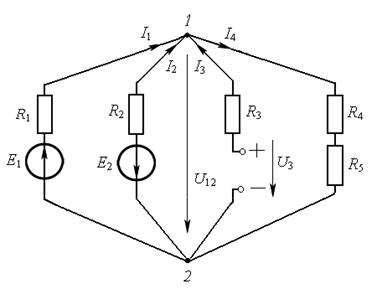
Рис.16.2

В частном случае схемы замещения без источников тока с двумя узлами по-

тенциал узла 1 при базисном узле 2, т. е. при 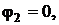равен напряжению меж-

ду узлами

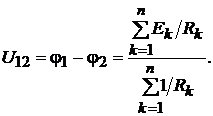(16.4)

Выражение (16.4) называется формулой межузлового напряжения.

Пример 31.В цепи (рис. 16.3) определить токи в ветвях методом узло-

вых потенциалов. Дано: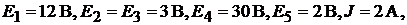

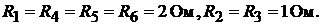
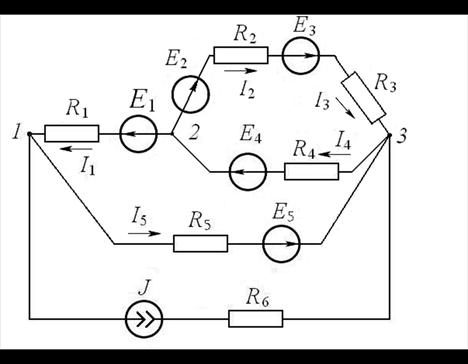
Рис. 16.3

Решение. В цепи три узла. Приняв потенциал одного из узлов равным нулю 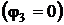, составим каноническую систему уравнений. Для определения потен-

циалов остальных узлов:

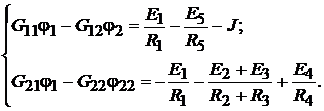
В этих уравнениях:

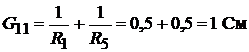
− сумма проводимостей всех ветвей, сходящихся в узле 1;

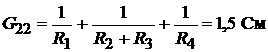
− сумма проводимостей всех ветвей, сходящихся в узле 2;

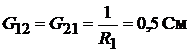
− сумма проводимостей ветвей, соединяющих узлы 1 и 2 .

После подстановки числовых значений имеем систему уравнений:

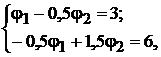
откуда

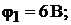
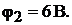
Токи в ветвях находим по закону Ома:

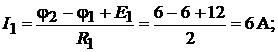
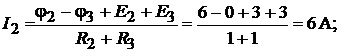
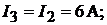
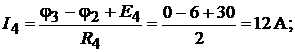
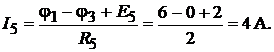
Для проверки правильности составления системы уравнений и её решения, запишем уравнения по второму закону Кирхгофа

,

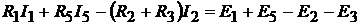или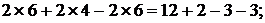

получаем тождество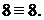

Пример 32.Найти токи в цепи (рис.16.4), если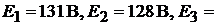

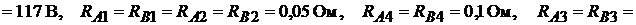
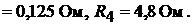Внутренние сопротивления источников ЭДС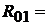

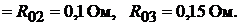Задачу решить методом узлового напряжения.

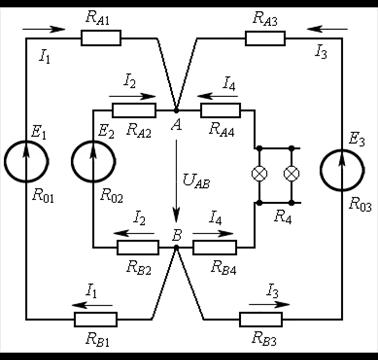
Рис. 16.4

Решение. Направления токов во всех ветвях выбираем одинаковым. Узловое напряжение определяем по формуле:

=

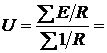
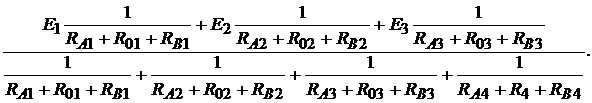
(16.1)

Эквивалентные сопротивления ветвей схемы:

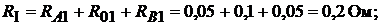
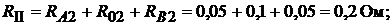
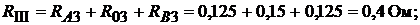
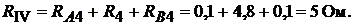
тогда выражение (16.1) можно записать так:

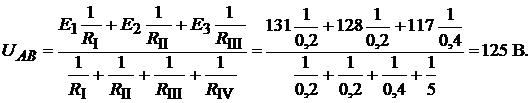
Токи в ветвях схемы:

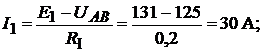
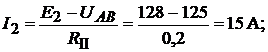
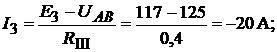
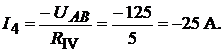
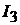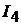Знак «−» означает, что действительные направления токов и проти-

воположны указанным в схеме.

Теперь, когда известны токи в ветвях, проверим соблюдение первого закона Кирхгофа:

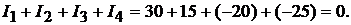
Пример 33.Методом узловых потенциалов определить все токи в ветвях электрической цепи (рис. 16.5):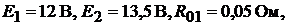

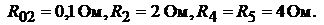
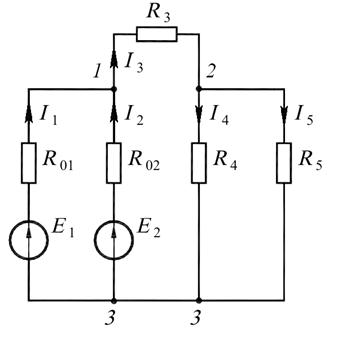
Рис. 16.5

Решение. В данной электрической схеме три узла, следовательно, нужно со-

ставить систему из двух уравнений относительно узловых потенциалов. Приняв потенциал узла 3 равным нулю, система уравнений примет вид:

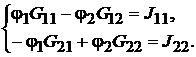
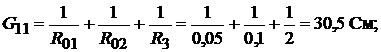
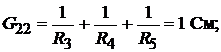
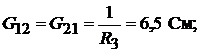
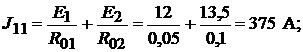
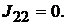
Решая систему уравнений с приведёнными значениями проводимостей и

расчётных токов, находим потенциалы узлов: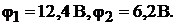

Токи в ветвях в соответствии с уравнением (4.5):

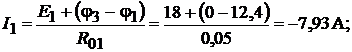
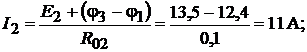
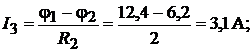
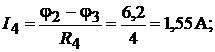
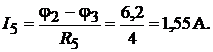
При расчёте токов в третьей, четвёртой и пятой ветвях ЭДС приняты рав-

ными нулю, так как в этих ветвях нет источников ЭДС.

Пример 34. Методом узловых потенциалов определить токи во всех ветвях схемы, изображённой на рис.16.6, а.

Дано: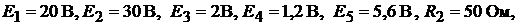

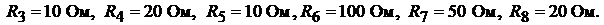
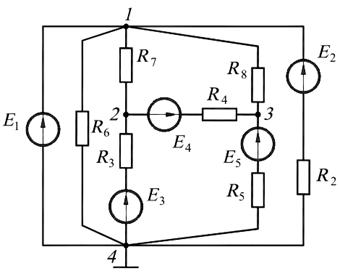
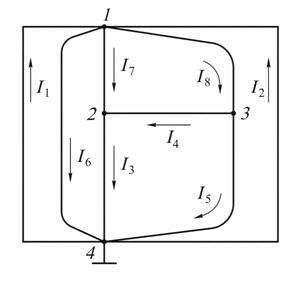
а б

Рис. 16.6

Решение.В цепи имеется ветвь с источником напряжения, не содержащая сопротивления. Целесообразно принять равным нулю потенциал одной из уз-

ловых точек, к которой подходит указанная ветвь, например потенциал узла 4 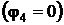. Тогдапотенциал точки 1 имеет значение, равно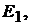е т.е. 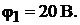Общее число уравнений 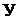равно двум 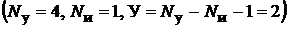. Таким образом, в данной задаче достаточно составить по методу узловых по-

тенциалов всего два уравнения для узлов 2 и 3.

Для узла 2: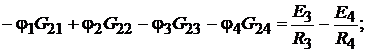

для узла 3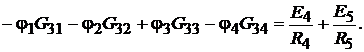

Подставляя в эти уравнения числовые значения сопротивлений, ЭДС, а так-

же значения 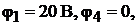после перегруппировки членов для двух неиз-

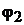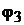вестных потенциалов и получим систему уравнений:

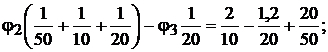
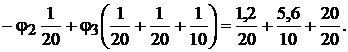
Решая эту систему уравнений, получим значения потенциалов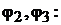

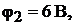
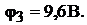
Применяя к отдельным ветвям формулы закона Ома, получим значения всех токов, которые нанесены на структурной схеме (см. рис. 16.6, б):

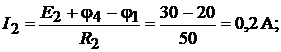
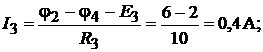
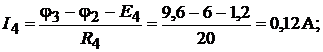
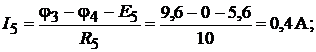
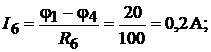
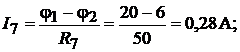
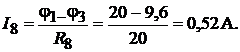
Обращаем внимание на то, что в ветви без сопротивления ток 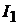не опреде-

ляется законом Ома и вычисляется на основании первого закона Кирхгофа:

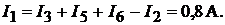
Пример 35.Методом узловых потенциалов найти токи в схеме цепи на рис. 16.7, а.

Дано: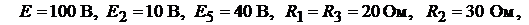

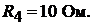
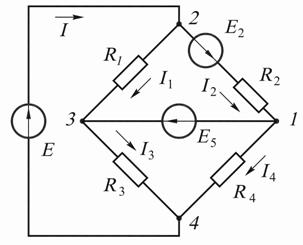
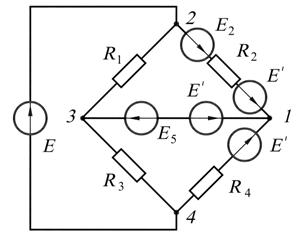
а б

Рис. 16.7

Решение. Всего в схеме четыре узла 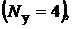две ветви, содержащие только

источники напряжения: ветви с ЭДС 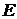и 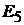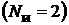. Тогда число уравнений, составляемых по методу узловых потенциалов, равно одному:

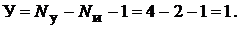
Однако при составлении уравнений согласно формулам типа (16.1) для лю-

бого из узлов войдут слагаемые, имеющие бесконечно большую проводимость.

Покажем, как обойти указанное затруднение.

Известно, что если во все ветви, примыкающие к какому-нибудь узлу, ввести одинаковые ЭДС, направленные к узлу (или от него), то это не окажет влияния на распределение токов в схеме, так как в уравнениях второго закона Кирхгофа для любого контура эти ЭДС взаимно компенсируются. Воспользовавшись этим свойством, введём во все ветви, примыкающие к узлу 1, ЭДС 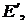направ-

ленные к этому узлу и равные 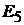(см. рис. 16.7, б). Теперь окажется, что в ветви 1–3 действуют две одинаковые и противоположно направленные ЭДС и их сумма равна нулю. Поэтому точки 1 и 3 равнопотенциальны и их можно закоротить (см. рис.16.8). Эта схема имеет три узла и содержит одну ветвь, имеющую только ЭДС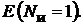

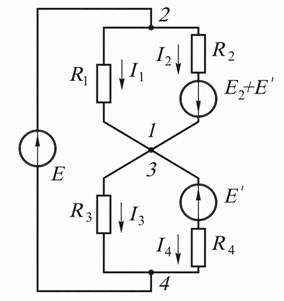
Рис. 16.8

Поэтому по методу узловых потенциалов надо составить всего одно уравне-

ние. Составим его для узла 1, приняв 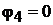. Тогда 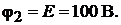Уравнение

для узла 1 будет иметь вид:

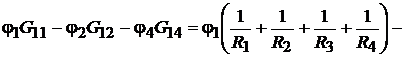
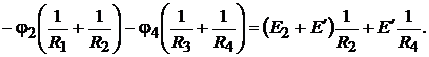
Подставляя сюда числовые значения, получим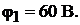

Найдём токи в ветвях исходной схемы по закону Ома:

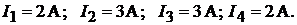
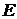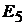Токи в ветвях с ЭДС и определяем по первому закону Кирхгофа:

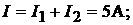
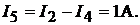
Пример 36. Определить выходное напряжение линейного потенциометра при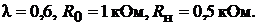

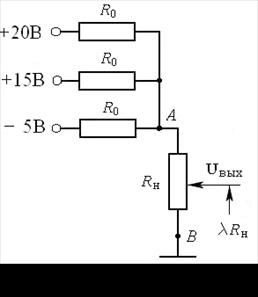
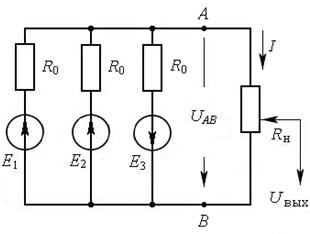
Рис.16.9 Рис. 16.10

Решение. Рассматриваемому потенциометру (рис. 16.9) соответствует схема

замещения (рис. 16.10). Напряжение 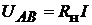определяется по формуле уз-

лового напряжения:

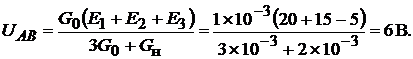
Следовательно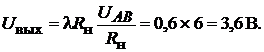

Пример 37. В цепи (рис. 16.11) известно показание вольтметра, равное 24 В, и значения параметров 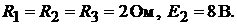Определить показание вольтметра в случае размыкания ветви с сопротивлением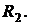

Решение. Решение основано на применении метода двух узлов.

1. Напряжение вольтметра 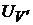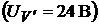по методу двух узлов:

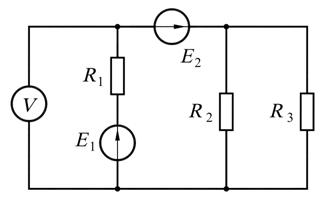
Рис. 16.11

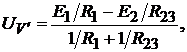
где 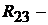сопротивление параллельного соединения 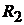и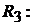

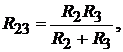
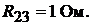
Из этого выражения можно определить ЭДС источника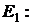

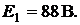
В случае обрыва ветви с сопротивлением 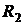показание вольтметра 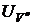оп-

ределяется в соответствии с выражением

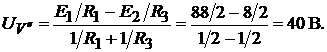
Все искомые переменные найдены.