Частота, или статистическая вероятность, события

Если произведена серия из 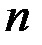опытов, в каждом из которых моглопоявиться или не появиться некоторое событие 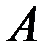, то частотой события 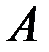в данной серии опытов называется отношение числа опытов, вкоторых появилось событие 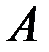, к общему числу произведенных опытов.

Частоту событий иногда называют его статистической вероятностью.Если обозначить ее знаком 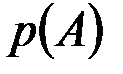, то частота события вычисляетсяна основании результатов опыта по формуле:

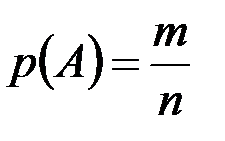, (2.1)

где 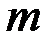– число появлений события 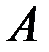; 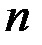–общее число произведенныхопытов.

Частота события всегда правильная дробь и изменяется в пределах .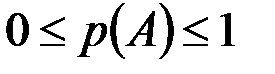

При небольшом числе опытов частота события носит в значительноймере случайный характер и может заметно изменяться от однойгруппы опытов к другой. При увеличении числа опытов частота событиявсе более теряет свой случайный характер, проявляет тенденциюстабилизироваться, приближаясь с незначительными колебаниями к некоторойсредней, постоянной величине –его вероятности.

Это свойство устойчивости частотесть одна из наиболее характерныхзакономерностей, наблюдаемых в случайных явлениях. Математическуюформулировку этой закономерности впервые дал Я. Бернуллив своей теореме, которая представляет собой простейшую форму законабольших чисел.

Связь между частотой события и его вероятностью – глубокая,органическая. Эти два понятия, по существу, неразделимы. Численнаяоценка степени возможности события посредством вероятности имеетпрактический смысл именно потому, что более вероятные события происходятв среднем чаще, чем менее вероятные.

Случайная величина

Одним из важнейших основных понятий теории вероятностей являетсяпонятие о случайной величине.

Случайной величинойназывается величина, которая в результатеопыта может принять то или иное значение, причем неизвестно заранее,какое именно.

Случайные величины, принимающие только отделенные друг отдруга значения, которые можно заранее перечислить, называются дискретнымислучайными величинами.

Случайные величины, возможные значения которых непрерывнозаполняют некоторый промежуток, называются непрерывными случайнымивеличинами.

Если классическая теория вероятностей оперировала по преимуществус событиями, то современная теория вероятностей предпочитаетоперировать со случайными величинами.Случайная величина в отличие от случайного события несет более полную информацию о явлении.

2.1.5. Практически невозможные
и практически достоверныесобытия

На практике обычно приходится иметь дело не с невозможными идостоверными событиями, а с так называемыми практически невозможнымии практическими достоверными событиями.

Практически невозможным событиемназывается событие, вероятностькоторого не в точности равна нулю, но весьма близка к нулю.

Практически достоверным событиемназывается событие, вероятностькоторого не в точности равна единице, но весьма близка кединице.

Вопрос о том, насколько мала должна быть вероятность события,чтобы его можно было считать практически невозможным, выходит зарамки математической теории и в каждом определенном случае решаетсяиз практических соображений в соответствии с той важностью, которуюимеет для нас желаемый результат опыта.

Основные теоремы

Назначение основных теорем

На практике обычно требуется определять вероятности событий,непосредственное экспериментальное воспроизведение которых затруднено.Такая оценка производится для того, чтобы выявить наиболее рациональныеконструктивные параметры элементов проектируемой, перспективнойтехники.

Поэтому, как правило, для определения вероятностей событийприменяются не непосредственные прямые методы, а косвенные, позволяющиепо известным вероятностям одних событий определять вероятностидругих событий, связанных с ними. Теория вероятностей, в основном,и представляет собой систему таких косвенных методов, пользованиекоторыми позволяет свести необходимый эксперимент к минимуму.

Применяя эти косвенные методы, мы всегда в той или иной формепользуемся основными теоремамитеории вероятностей. Этих теоремдве: теорема сложения вероятностей и теорема умножения вероятностей.

Перед тем как формулировать основные теоремы, введем вспомогательныепонятия о сумме событий и произведении событий.

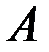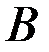Суммой двух событий и называется событие 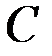, состоящее ввыполнении события 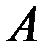или события 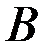, или обоих вместе.

Если события 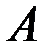и 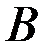несовместны, то появление обоих этих событийвместе отпадает, и сумма событи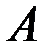й и 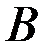сводится к появлению илисобытия 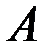, или события .

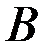Другими словами, суммой двух событи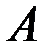й и 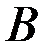называется событие 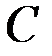, состоящее в появлении хотя бы одного из событи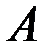й и .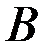

Суммой нескольких событий называется событие, состоящее впоявлении хотя бы одного из этих событий.

Произведением двух событи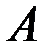й и 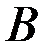называется событие 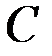, состоящеев совместном выполнении события 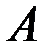и события .

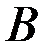Произведением нескольких событий называется событие, состоящеев совместном появлении всех этих событий.

При пользовании понятиями суммы и произведения событий частооказывается полезной наглядная геометрическая интерпретация этихпонятий, которая приведена на рис. 2.1.

Рисунок 2.1 –Сумма двух событий (а); произведение двух событий (б)