Числовые характеристики СЛУЧАЙНОГО ВЕКТОРА

Для двумерного случайного вектора (X, Y) вводятся следующие числовые характеристики.

Начальным моментом порядка r + s случайного вектора (X, Y) называется действительное число n_r,s, определяемое формулой:

n_r,s = M[X^r Y^s] =

Начальный момент n_r,s существует, если интеграл (соответственно ряд) в правой части равенства абсолютно сходится. В частности, n_r,0 = M[X^r] - соответствующие начальные моменты компоненты X. Вектор с неслучайными координатами (m_X, m_Y) = (n_1,0, n_0,1) называется математическим ожиданием случайного вектора (X, Y) или центром рассеивания.

Центральным моментом порядка r + s случайного вектора (X, Y) называется действительное число m_r,s определяемое формулой

m_r,s = M[(X-m_X)^r (Y-m_Y)^s] =

Центральный момент m_r,s существует, если интеграл (соответственно ряд) в правой части равенства абсолютно сходится. Вектор с неслучайными координатами (D_X, D_Y) = (m_2,0, m_0,2) называется дисперсией случайного вектора.

Центральный момент m_1,1 называется корреляционным моментом (ковариацией): K_XY = M[ ] = M[(X-m_X)×(Y-m_Y)] = M[XY]-m_X m_Y.

Коэффициентом корреляции двух случайных компонентов X и Y случайного вектора является нормированная ковариация

r_XY = K_XY/(s_Xs_Y). Свойства ковариации (и коэффициента корреляции):

1. K_XX = D_X, K_YY = D_Y, (r_XX = r_YY = 1);

2. K_XY = K_YX, (r_XY = r_YX);

3. |K_XY| £ , (|r_XY | £ 1).

Ковариационный момент и коэффициент корреляции определяет степень линейной зависимости между X и Y. Условие |r_XY | = 1 необходимо и достаточно, чтобы СВ X и Y были связаны линейной зависимостью Х = a×Y + b, где a и b - константы. СВ, для которых K_XY = 0 (r_XY = 0), называются некоррелированными. Из независимости случайных величин Х и Y вытекает их некоррелированность (обратное, вообще говоря, неверно).

Условным математическим ожиданием компоненты Х при условии, что Y приняла одно из своих возможных значений y_j, называется действительное число определяемое формулой:

m_X/Y = M[X/Y = y_j] =

где Р{X = x_i /Y = y_j} = , p_ij = Р{X = x_i ,Y = y_j}.

Условной дисперсией компоненты Х при условии, что Y приняла одно из своих возможных значений y_j, называется действительное число определяемое формулой:

D_X/Y = D[X/Y = y_j] =

Приведенные выше формулы для числовых характеристик двумерного случайного вектора без труда обобщаются на случай n-мерного случайного вектора (Х₁, Х₂, ..., Х_n). Так, например, вектор с неслучайными координатами (m₁, m₂, ..., m_n), где m_i - математическое ожидание СВ Х_i, определяемое формулой

m_i = M[X_i] = , называется центром, рассеивания случайного вектора.

Ковариационной матрицей n-мерного случайного вектора 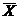= (Х₁, Х₂, ..., Х_n) называется симметрическая матрица, элементы которой представляют собой ковариации соответствующих пар компонент случайного вектора:

K = ,

где Кij = M[ ] - ковариация i-й и j-й компонент. Очевидно, что Кii = М[Xi2] -дисперсия i-й компоненты.

Корреляционной матрицей n-мерного случайного вектора называется симметрическая матрица, составленная из коэффициентов корреляции соответствующих пар компонент случайного вектора:

C = ,

rij = - коэффициент корреляции i-й и j-й компоненты.

Задача 1. Закон распределения случайного вектора (X, Y) задан в следующем виде:

Y X	1	2	3
1	1/9	1/9	1/9
2	0	1/6	1/6
3	0	0	1/3

1. Вычислить условное математическое ожидание M[X/Y = 2] и дисперсию D[X/Y = 2].

2. Найти центр рассеивания случайного вектора (X, Y).

3. Построить ковариационную и корреляционную матрицы.

Задача 2. Координаты X, Y случайного положения точки на плоскости имеют

совместное равномерное распределение внутри области G = {(x, y) | -1£ x £ 2, 1 £ y £ 2}.

Записать общее выражение для ПР и для ФР вероятности случайного вектора (X,Y).

Найти центр рассеивания (m_X, m_Y)и вычислить дисперсию (D_X, D_Y) совместного распределения координат.

Построить ковариационную и корреляционную матрицы.

ЗАКОН БОЛЬШИХ ЧИСЕЛ

Следующие утверждения и теоремы составляют основу законов, объединенных общим названием закон больших чисел.

Первое неравенство Чебышева. Если СВ X ³ 0 имеет конечное значение m = M[X], то для любого e > 0 справедливо:

P{X ³ e} £ m/e или P{X < e} > 1 - m/e.

3 Для наглядности проведем доказательство для СВНТ X с ПР f(x), хотя это остается справедливым и для СВДТ. Так как

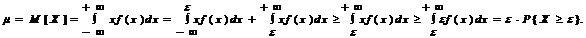
Тогда P{X ³ e} £ m/e, что и требовалось показать. 4

Второе (основное) неравенство Чебышева. Если СВ X имеет конечные значения m = M[X] и s² = D[X], то для любого e > 0 справедливо:

P{ôX - mô ³ e} £ s²/e² или P{ôX - mô < e} > 1 - s²/e².

3 Проведем доказательство для СВНТ X с ПР f(x). Так как

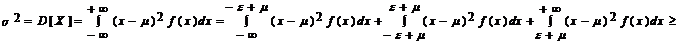
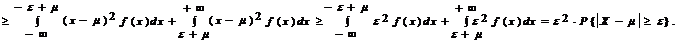
Тогда P{ôX - mô ³ e} £ s²/e², что и требовалось показать. 4

Последовательность СВ X₁, X₂, ..., X_n, ... называется сходящийся по вероятности при n ® ¥ к СВ X (обозначение: 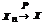при n ® ¥), если для любого, сколь угодно малого e > 0 справедливо 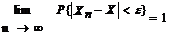, или, иными словами, для любых, сколь угодно малых чисел e > 0 и d > 0 найдется номер k, что для всех n > k выполняется условие:

P{ôX_n - Xô < e} > 1 - d.

Теорема (Закон больших чисел в форме Чебышева). Если попарно независимые СВ X₁, X₂, ..., X_n, ... имеют конечные значения M[X_i] = m_i и D[X_i] = s_i²£ s², то для любого e > 0 справедливо следующее:

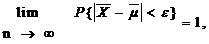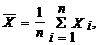
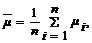где или 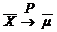при n ® ¥.

3 Пусть СВ 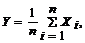следовательно математическое ожидание и дисперсия этой СВ определяется следующим образом

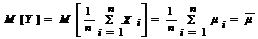и .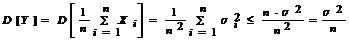

Из второго неравенства Чебышева следует, что P{ôY - M[Y]ô < e} > 1 - D[Y]/e² ³ 1 - c²/n, где c = s/e > 0.

Тогда при n ® ¥ для любого e > 0 вероятность P{ô 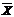- 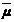ô < e} ® 1, что и требовалось показать. 4

Следствие. Если в условии теоремы СВ X₁, ..., X_n, ... имеют одинаковые значения M[X_i] = m, то для любого e > 0 справедливо следующее:

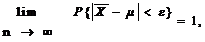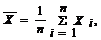где или 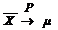при n ® ¥.

Теорема (Закон больших чисел в форме Бернулли). Пусть СВ К - число “успехов” в n испытаниях по схеме Бернулли. Тогда при n ® ¥ частота “успехов” сходится по вероятности к p, где p - вероятность “успеха” в одном испытании, т.е.:

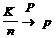при n ® ¥ или 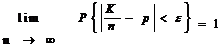для любого e > 0.

3 Пусть СВ X_i подчиняется закону распределения Бернулли, следовательно M[X_i] = p и D[X_i] = p×q. Так как 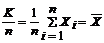, тогда из следствия теоремы получаем для любого e > 0

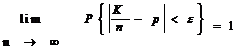или 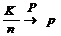при n ® ¥, что и требовалось показать. 4

Задача 1. Пусть СВ X подчиняется закону E_x(1). С помощью неравенств Чебышева оценить вероятности

P{ôX - M[X]ô < a× 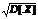} для a = 1, 2, 3. Сравнить эти оценки с точными значениями.