Уточнение понятия алгоритма. Тезис Чёрча

Неразрешимость некоторых алгоритмических проблем поставила перед математиками трудную задачу точного определения понятия “алгоритм”. Решение этой задачи было получено в 30-х гг. XX в. в двух формах:

1) решение основано на понятии рекурсивной функции;

2) решение основано на описании точно очерченного класса вычис-лительных процессов, реализуемых на машинах Тьюринга.

Отправляясь от аксиоматики Гильберта, Гёдель описал класс всех рекурсивных функций как класс всех арифметических функций, определи-мых в некоторой формальной системе. Исходя из других предпосылок, Чёрч пришёл в 1936 г. к тому же классу арифметических функций. Анализ идей, которые привели к этому классу функций, позволил Чёрчу выдвинуть гипотезу о том, что класс рекурсивных функций тождествен классу всюду определённых вычислимых функций (тезис Чёрча). Так как понятие “вычислимые функции” точно не определено, то тезис Чёрча доказать нельзя. Этот тезис является научной гипотезой, в пользу которой высказан ряд важных доводов и которую не удалось опровергнуть. Одним из таких доводов является то, что различные уточнения понятия “алгоритм”, сделанные разными авторами, оказались равносильными. Так, например, нормальный алгоритм Маркова оказался сводимым к ОРФ.

Для того, чтобы охватить бесконечно длящиеся процессы перера-ботки исходных данных, Клини ввёл понятие частично рекурсивной функ-ции и высказал гипотезу, что все частичные (т. е. не обязательно опреде-лённые для всех значений аргументов) функции, вычислимые посредством алгоритмов, являются частично рекурсивными. Более общая гипотеза Клини также недоказуема, как и гипотеза Чёрча. В дальнейшем под гипотезой Чёрча будет пониматься расширенная Клини формулировка.

Тезис Чёрча оказался достаточным, чтобы придать необходимую точность формулировкам алгоритмических проблем и в ряде случаев сделать возможным доказательство их неразрешимости. Отметим, что понятие рекурсивной функции строгое. Поэтому обычная математическая техника позволяет иногда непосредственно доказать, что решающая задачу функция не может быть рекурсивной. Именно этим путём Чёрчу удалось первому доказать неразрешимость основной алгоритмической проблемы логики предикатов - проблемы тождественной истинности формул исчисления высказываний.

Точное описание класса частичных рекурсивных функций вместе с тезисом Чёрча даёт одно из возможных решений задачи об уточнении понятия алгоритма. Однако это решение не вполне прямое, так как понятие вычислимой функции является вторичным по отношению к понятию алго-ритма. Спрашивается, нельзя ли уточнить непосредственно само понятие алгоритма и уже затем при его помощи определить точно и класс вычисли-мых функций? Это было сделано Постом и Тьюрингом независимо друг от друга и почти одновременно с упомянутыми выше работами Чёрча и Клини.

Основная мысль Поста и Тьюринга заключалась в том, что алгорит-мические процессы - это процессы, которые может осуществлять подхо-дяще устроенная “машина”. В соответствии с этой мыслью ими были описаны в точных математических терминах довольно узкие классы машин, но на этих машинах оказалось возможным осуществлять или имитировать все алгоритмические процессы, которые фактически когда-либо описывались математически. Алгоритмы, осуществимые на данных машинах, было предложено рассматривать в качестве математических “представителей” вообще всех алгоритмов.

Несложные выкладки показали, что класс функций, вычислимых на этих машинах, в точности совпадает с классом всех частично рекурсивных функций. Тем самым было получено ещё одно фундаментальное подтверждение тезиса Чёрча. Машины Поста и Тьюринга отличались несущественно и в дальнейшем стали называться машинами Тьюринга.

Интуитивное определение как численных, так и логических алгорит-мов похоже: в обоих случаях алгоритм определяется как система правил для решения определённого класса задач, которая обладает свойствами детерминированности, массовости и результативности.

Для уточнения понятия алгоритма в рассмотрение введен нормальный алгоритм Маркова; эта форма алгоритма удобна для специалиста по логике. Для тех же специалистов, которые имеют дело с численными алгоритмами, удобней иметь стандартный аппарат, более близкий к их естественной форме. Таким аппаратом является машина Тьюринга.

В процессе построения теории численных алгоритмов было выяснено, что любой логический алгоритм можно простыми методами свести к числен-ному алгоритму. По мере усовершенствования этих методов стало ясно, что вообще любой алгоритм может быть всегда сведен к численному алгоритму.

Таким образом, теория численных алгоритмов (это понятие тожде-ственно понятию “теория вычислимых функций”) стала универсальным аппаратом для исследования всех алгоритмических проблем.

Поскольку понятия “алгоритм” и “вычисление значений арифмети-ческой функции” тождественны, то в соответствии с тезисом Чёрча задача оказывается алгоритмически разрешимой лишь тогда, когда арифметиче-ская функция, к вычислению которой сводится задача, оказывается общерекурсивной. Иначе: алгоритм существует лишь тогда, когда может быть построена общерекурсивная функция (просто рекурсивная функция).

Наоборот, в силу тезиса Чёрча алгоритмическая неразрешимость проблемы означает, что арифметическая функция, к вычислению которой сводится задача, не является рекурсивной.

Заключение

Рассмотрены 3 модели вычислений: ассоциативные исчисления (для логических вычислений), рекурсивные функции (для численных вычисле-ний) и машины Тьюринга (для общего случая вычислений, включая сим-вольную обработку). Последняя модель используется также для доказа-тельства существования алгоритма решения класса задач. Алгоритмы, соответствующие этим моделям, равносильны и могут быть получены друг из друга. Существуют и другие, специализированные модели.

Уточнение понятия ²алгоритм² основано на использовании тезиса Чёрча (классы ВФ и ОРФ равны) и на строгом определении двух объектов: 1) класс ОРФ; 2) МТ. В 1-м случае уточнение косвенное, во 2-м – прямое.

Исчисление – это не алгоритм, однако упорядочение допустимых подстановок, предложенное А.А. Марковым, позволило создать нормальный алгоритм; к нормальному алгоритму может быть сведен любой вычислительный процесс, удовлетворяющий признакам 1-5 (см. Введение) – это ещё одна формулировка, эквивалентная тезису Чёрча.

Различные формулировки тезиса Чёрча эквивалентны, что говорит об их глубокой общности, суть которой состоит в том, что вычислительный процесс для некоторого класса задач может быть построен, если его можно описать рекурсивными функциями. Проверка такой возможности может быть проведена на соответствующим образом построенной МТ.

Несуществование алгоритма для того или иного класса задач не означает неразрешимости вообще; это означает лишь, что рассматриваемый класс задач настолько широк, что единого эффективного метода для решения всех задач данного класса не существует.

Рекомендуем читателю ознакомиться с [6, 7, 8] для более глубокого понимания материала данной главы.

Контрольные вопросы. Упражнения

1. Чем отличаются логические алгоритмы от численных?

2. Чем отличается исчисление от алгоритма?

3. Какие исчисления, в том числе ассоциативные, знаете Вы?

4. В чём заключается идея нормального алгоритма А.А. Маркова?

5. Каково соотношение множеств вычислимых, элементарных, примитивно-рекурсивных и общерекурсивных функций?

6. За счёт чего расширен класс ПРФ до класса ОРФ?

7. Что общего и в чём различие классов ПРФ и ОРФ?

8. Почему недоказуема гипотеза Чёрча?

9. Заданы начальное слово P₁=abcbcbab и система допустимых под-становок: 1. ab®cd; 2. bcd®d; 3. dc®abc; 4. ac®ca. Постройте дедуктив-ную цепочку преобразований слов в соответствии с нормальным алгорит-мом А. А. Маркова и объясните результат.

10. Определите примитивно-рекурсивные функции j(y, x), заданные своими схемами вычислений и начальными значениями:

а) j(y’, x)=j(y, x)x¢, j(0, x)=1; е) j(y¢, x)=j¢(y, x)x, j(0, x)=x;

б) j(y¢, x)=j(y, x)+x, j(0, x)=0; ж) j(y¢, x)=j¢(y, x)+x, j(0, x)=0;

в) j(y¢, x)=j(y, x)+x, j(0, x)=x;з) j(y¢, x)=(j(y, x)+x)¢, j(0, x)=x;

г) j(y¢, x)=j(y, x)x,  j(0, x)=1; и) j(y¢, x)=(j(y, x)+x)¢x,  j(0, x)=0;

д) j(y¢, x)=j(y, x)x, j(0, x)=x; к) j(y¢, x)=j¢(y, x)+x¢, j(0, x)=1.

11. Используя условия п. б) и в) предыдущего упражнения, запишите вид функций, определяемых соответствующими выражениям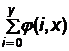и

и 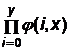.