Результаты решения (AW) задачи в виде таблицы и графика
| Z/W | 1,5 | 4,5 | 7,5 | 10,5 | 13,5 | ||||||
| 0,2 | 7.27 | 8.19 | 10.24 | 14.53 | 17.5 | 10.75 | 6.3 | 4.15 | 2.97 | 2.25 | |
| 0,45 | 7.17 | 7.65 | 8.36 | 8.69 | 7.78 | 4.41 | 3.29 | 2.53 | |||
| 0,7 | 6.93 | 6.62 | 5.95 | 4.03 | 3.2 | 2.56 | 2.07 | 1.7 |
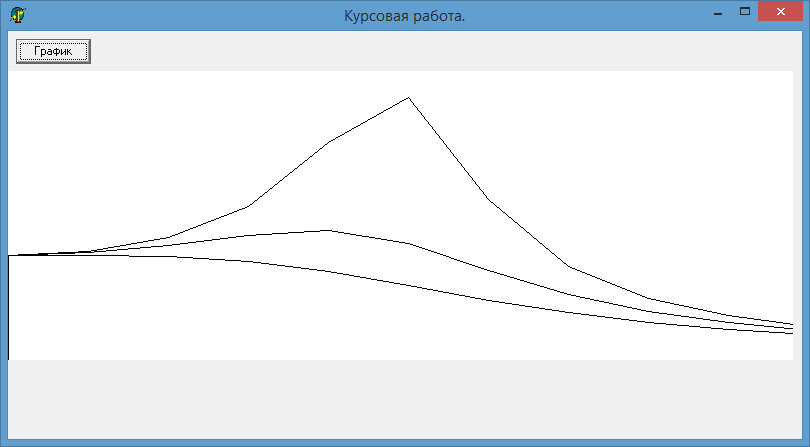
Краткий анализ результата
При увеличении относительного коэффициента затухания (z) и одинаковых значениях частоты (W) амплитуда (A(W)) уменьшается.
ЗАДАЧА 3. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ АНАЛИТИЧЕСКИ
ЗАДАННОЙ ФУНКЦИИ.
По заданному выражению аналитической функции f(x) вычислить приближенно определенный интеграл от этой функции на заданном интервале [a,b]:
 ,
,
используя квадратную формулу парабол (метод Симпсона):

Исходные данные
| Функция | Интервал | Число разбиений | ||
| f(x) | a | b | n1 | n2 |
 |
Таблица принятых обозначений переменных
| i | N1 | N2 | S1 | S2 | H1 | H2 | I1 | I2 |
| a | b | Sum1 | Sum2 |
Алгоритм решения задачи
1.Для основного выражения используем функцию f.
2.По формуле Симпсона вычисляем 2 интеграла для различных разбиений.
3.Выводим результат на экран.
Текст программы
Type
fact = record
a:real;
b:real;
end;//для удобства. В дальнейшем все будет понятно
vari:integer;
n1,n2:integer;
s1,s2:fact;
h1,h2,i1,i2,a,b:real;
sum1,sum2:real;
functionf(x:real):real;
Begin
f:=ln(x+1)/(1+sqr(x));//данная функция
end;
Begin
a:=0;
b:=1;
n1:=12;
n2:=24;
h1:=(b-a)/n1;
h2:=(b-a)/n2;//высота каждого сектора при разбиении
fori:=1 to(n1 div2) do //часть формулы Симпсона. В этом цикле мы находим сумму  .
.
Begin
s1.a:=a+(i-1)*2*h1+h1;// 
s1.b:=a+(i-1)*2*h1; //  {числа от которых найдем результат функции}
{числа от которых найдем результат функции}
sum1:=sum1+(4*f(s1.a)+2*f(s1.b));//собственно сумма
end;
I1:=h1/3*(-f(a)+sum1+f(b)); //интеграл по формуле Симпсона
fori:=1 to(n2 div2) do
Begin
s2.a:=a+(i-1)*2*h2+h2;
s2.b:=a+(i-1)*2*h2;
sum2:=sum2+(4*f(s2.a)+2*f(s2.b));
end;
I2:=h2/3*(-f(a)+sum2+f(b));//то же самое проделываем с другим разбиением
writeln('Интегралы при числе разбиений n1 и n2 равных ', n1,' и ',n2,' соответственно');
write('I1 = ',i1:0:6,', I2 = ',i2:0:6);//вывелирезультат.
readln;
end.
Результаты решения задачи в виде таблицы
| Интегралы при числе разбиений n=10 | 0.272200 |
| Интегралы при числе разбиений n=20 | 0.272198 |
Краткий анализ результата
При уменьшении числа разбиений (n) значение функции после интегрирования увеличивается, хотя для выявления разницы нужен точный подсчёт.
ЗАДАЧА 4. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ
УРАВНЕНИЙ С ЗАДАННОЙ ТОЧНОСТЬЮ.
По заданному нелинейному уравнению
F(x)=0,
где F(x) – некоторое нелинейное аналитическое выражение, определенное на интервале
[a, b],
вычислить корни этого уравнения с требуемой точностью E методом половинного деления (дихотомии).
Исходные данные.
| Функция | Интервал | Точность | ||
| f(x) | a | b | N | E |
 | 10-5 |
Таблица принятых обозначений переменных
| i | x | a | b | res | n | lim |
Алгоритм решения задачи
1.Для удобства объявим функцию, в которой будет храниться заданная функция.
2.С помощью оператора repeat выполняем следующую последовательность действий:
a).Вычисляем середину отрезка;
b). Вычисляем F(x).
с).Если F(x)>0 и F(a)>0 или F(x)<0 и F(a)<0 (т.е. перемена знака функции F(x) не произошла), то задаем a=x (т.е. перемещаем левую границу интервала в середину), уменьшая интервал вдвое и исключая при этом левую половину, на которой либо нет корней, либо есть четное число корней, иначе задаем b=x (исключаем правую половину интервала).
d).Проверяем условие b-a<E.Если оно истинно,считаем,что последнее значение x и будет корнем уравнения с заданной точностью E и выходим из цикла.Если он не выполняется,то возвращаемся в начало цикла (пункт а).) с новыми значениями интервала.
3.Выводим результаты вычислений.
Текст программы
unit Unit4;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Math, StdCtrls;
type
TForm1 = class(TForm)
Label2: TLabel;
Edit1: TEdit;
Label3: TLabel;
Edit2: TEdit;
Label4: TLabel;
Edit3: TEdit;
Button1: TButton;
Label5: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
E:real;
implementation
{$R *.dfm}
function f(x:real):real;
begin
f:=x-2+sin(1/x);
end;
function f1(x:real):real;
begin
f1:=(f(x+e)-f(x))/e;
end;
procedure TForm1.Button1Click(Sender: TObject);
var a,b,x:real;
begin
a:=strtofloat(Edit1.text);
b:=strtofloat(Edit2.text);
E:=strtofloat(Edit3.text);
x:=a;
While (abs(x-b)>e) do
begin
x:=b;
b:=x-f(x)/f1(x);
end;
Label5.caption:= 'X= '+floattostr(x);
end;
end.
